-离散数学-期末练习题解析_xa(x)等价命题

A. ∀x( (P(x) ∨ Q(x) ) ⇔ ∀xP(x) ∨ ∀xQ(x)
B. ∀x(P(x) ∧ Q(x)) ⇔ ∀xP(x) ∧ ∀xQ(x)
C. ∃x(P(x) ∨ Q(x) ) ⇔ ∃xP(x) ∨ ∃xQ(x)
D. ∀x(P(x)∧Q) ⇔ ∀xP(x)∧Q

A

11. 设个体域D={a,b},与公式彐xA(x)等价的命题公式是( C )
    A.A(a) ∧A(b
    B.A(a)→A(b)
    C. A(a) ∨ A(b)
    A(b)→A(a)
12. 设X={Ø,{a}{a,Ø}},则下列陈述正确的是(
    A. a∈X
    B. {a,Ø}⊆X
    C. {{a,Ø}}⊆X
    D. {Ø}∈X

C
元素与集合的关系用属于
集合与集合的关系用包含
A中用的是属于，但a不是X的元素，因为需要把整个集合{a}看成X的 一个元素
B用的是属于，说明得把{a,Ø}看成一个集合，a和Ø都得是X的元素，a不是X的元素，所以不正确，也可解释作{a,Ø}只是X的一个元素，并不是指一个集合
C正确，有两重括号，第一个括号内的{a,Ø}就是X的一个元素，{{a,Ø}}就是X的一个子集
D中用的是属于，说明整个{Ø}被看成是一个元素，但X中只有Ø而没有{Ø}

13. 有向图D是连通图,当且仅当( D ）
    A. 图D中至少有一条通路
    B. 图D中有通过每个顶点至少一次的通路
    C. 图D的连通分支数为一
    D. 图D中有通过每个顶点至少一次的回路

D
这里的连通图应该指的是强连通图
对C要特别注意一下，有第一章的命题逻辑我们知道“当且仅当”指的是充要条件，连通图的连通分支数确实为一，但连通分支数为一的并不代表是连通图，所以C是错的

14. 设A={a,b,c},则下列是集合A的划分的是 ( B)
    A. {{b,c},{c}}
    B. {{a},{b,c}}
    C. {{a,b},{a,c}}
    D. {{a,b},c}

B

我们可以知道π是一个子集族，里面都应该是子集，D错误
然后每个子集不能有重复的元素，AC错误

15. 下列谓词公式中是前束范式的是( D )
    A. ∀xF(x)∧¬(∃x)G©
    B. ∀xP(x) ∧ ∀yG( y)
    C. ∀x(P(x)→∃yQ(x,y)
    D. ∀x∃y(P(x)→Q(x,y))

D
前束范式就是所有的量词都在前面

16. 设M={x | f1(x)=0},N={x | f2(x)=0},则方程f1(x)*f2(x)=0的解为（ B　）　
    A. M∩N
    B. M∪N
    C. M⊕N
    C. M-N

f1(x)*f2(x)=0只有=要有一个为0 其结果就为0
显然是M和N的并集

在数学中，群表示一个拥有满足封闭性、满足结合律、有单位元、有逆元的二元运算的代数结构，包括阿贝尔群、同态和共轭类。
设G是一个群，则

1. G满足消去律（左消去和右消去），即∀a,b,c∈G,若ab=ac,则b = c
2. 任意一个元素的逆元的逆元是其本身,A 正确
3. (ab)^-1 = b ^-1 * a ^-1, C错误
   其余请看群的详细介绍

18. 在整数集合Z上，下列定义的运算满足结合律的是（ ）
    A. ab=b+1
    B. ab=a-1
    C. ab=ab-1
    D. ab=a+b+1

D
如果满足结合律，则(a*b)*c=a*(b*c)

19. 设简单图G所有的结点的度数之和为50，则G的边数为（ ）
    A. 50
    B. 25
    C. 10
    D. 5

B
既不含平行边也不含环的图为简单图
由握手定理：度数之和为变数的2倍，变数为25

20. 设简单无向图G是一个有5个顶点的4-正则图，则G有（ ）条边。
    A. 4
    B. 5
    C. 10
    D. 20

C
正则图是指各顶点的度均相同的无向简单图
有题意，度数之和为5*4=20，边数=20 / 2 = 10

21. 设集合A={1，2，3，4}，A上的等价关系R= {<1,1>, <.3,2>,<2,3>,<4,4>} U IA (恒等关系),则对应于R的划分是（ ）
    A. { {1}，{2，3}，{4} }
    B. { {1，3}，{2，4} }
    C. { {1，3}，{2}，{4} }
    D. { {1}，{2}，{3}，{4} }

A
IA表示恒等关系，设A={a,b,c}，则其上关系R={<a,a>,<b,b>,<c,c>}，R便是恒等关系
本题中IA中应该是补齐<2,2><3,3>，2和3应该被分到了另外一块，应该选A

D
在数学中，若对某个集合的成员进行一种运算，生成的仍然是这个集合的元素，则该集合被称为在这个运算下闭合。
比较最大数，得到的结果还是在A中
比较最小数，结果还是在A中
最大公约数，1和10的最大公约数为1，L为任意数字，与其他的数求最大公约数，都可以在1，2，10，L中取得
若L为3，3和10 的最小公倍数为30，不在A中，D不是封闭的

C
先看看满射，单射和双射的定义

F的关系是一一对应的，满足单射，但ｆ的值域中没有ｄ，不满足满射的条件

B
割点和割边指拿掉某个点或某些边，连通分支数增加
割点集和桥指拿掉某些点或某条边，连通分支数增加

D
经过图的每一条边且仅一次并且行遍图中的每个顶点的回路（通路），称为欧拉回路（欧拉通路），存在欧拉回路的图，称为欧拉图
无向图G有欧拉回路当且仅当G是连通图且无奇度顶点
只有欧拉通路当且仅当图G恰有２个奇度顶点，这两个点为欧拉通路的端点

A
叶子结点度数只有１，显然不对
其余都是树的等价条件

A
幂集的个数为2^n

C
握手定理的推论：任何图中的度数为奇数的顶点的个数为偶数
可以排除A和D
对B选项，总共有6个点，有两个度数为5的点，而度数为5说明它与其他顶点都相连，反过来其它每个点都会与这两个点相连，度数不可能小于2，B错误

欧拉图中没有奇度顶点，排除A,C
哈密顿图中任意两个不相邻的顶点度数之和>=n-1
D中选择右边的两个度数为2的顶点，度数之和为4<6,D不存在哈密顿回路

C
共有6*3=18度
边数=度数之和 / 2 = 9

B
自反是全部顶点都有自环
反自反是全部顶点都没有自环
对称是顶点之间有边的话，全是双向边
反对称是顶点之间有边的话，全单向边

B

R2是将R1的单向边补成了双向边，应该是对称闭包

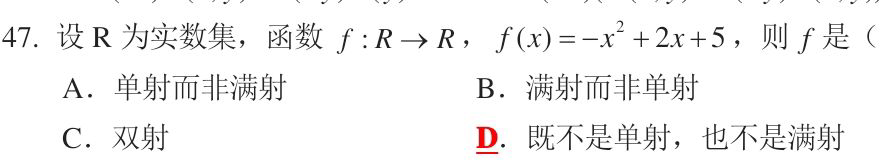
D
f(x)中x与y并不是一一对应，所以不是单射，f(x)的最大值6，并不是实数集R，不是满射

C
A,B,D中都有奇度顶点，无法构成欧拉图

二. 填空题

1. 命题公式¬(p→q)的成真赋值_____,成假赋值____.

真：1 0 , 假： 0 0, 0 1, 1 1.

2. 命题公式(p ∨ q)→p的成真赋值____,成假赋值____.

真：0 0, 0 1 , 1 1. 假：1 0.

3. 命题公式p→(p∧q)的成真赋值____,成假赋值_____.

真：00，01，11，假：10

4. 公式( ∀x)( ∀x)( P(y)→Q(x,z) ) ∧ (∃y)R(x,y)约束变元为____,自由变元为____.

x,y x,z
对左边部分 ∀x ∀y说明x,y是约束出现的，z是自由的
对右边∃y说明y是约束的，x是自由的

5. 公式 ∀x(P(x) ∨ ∃yR(x) )→Q(x,z)约束变元为____,自由变元为_____.

约束: x,y
自由: x,z

6. 设A = {a,b,{a,b} }, B={a,b},则B-A=____,A⊕B=_____.

B-A=Ø
A⊕B={ {a,b} }

7. 设A={1，2，3}，A上的关系R={<1,2>,<2,1>},则对称闭包s( R ) = ______,传递闭包t( R )= _____。

s( R ) = {<1,2>,<2,1>} //本身就是双向边，无需改动
t( R )={<1,2>,<2,1>,<1,1>,<2,2>} //<1,2><2,1>添加<1,1>,同时也可以看成<2,1>,<1,2>要添加<2,2>

8. 设A={a,b,{a,b} },B= {a,b,c}，则A⊕A= ______,A⊕B=______.

则A⊕A=Ø
A⊕B={{a,b},c}

9. 一颗无向树的顶点数n与边数m的关系是____,6阶无向连通图至多有____颗不同的生成树。

m = n-1
6颗

10. 设f(x)=x-1,g(x)=x^2,则复合函数(f g)(x)=_____,(g f)(x) =____.

统一规定为右复合
(f g)(x) = g(f(x))=(x-1)^2
(g f)(x) =f(g(x))=x^2-1

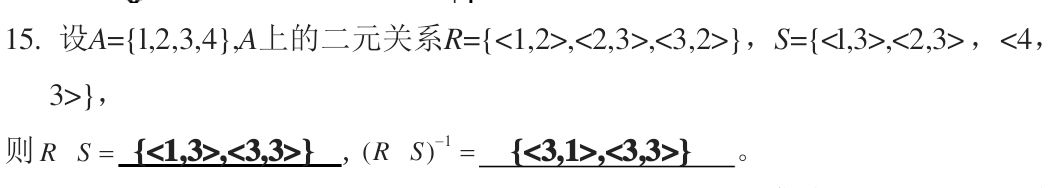
合成
R°S={<zx,z>|∃y<x,y>∈R∧∃z<y,z>∈S}

18. 一颗无向树的顶点数n与边数m的关系是_____,设G是具有8个顶点的数，则G增加____条边才能把G变成完全图。

m =n-1
21条
无向完全图 边数m = (n*(n-1))/2
有向完全图 边数m = (n*(n-1))
总边数m = 8*7/2=28，树G有7条边
增加28-7=21条

三、 计算题

2.

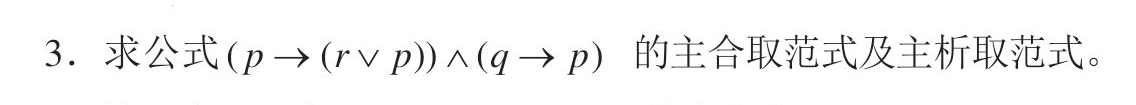
4. 一棵(无向)树有2结点的度为2,1个结点的度为3,3个结点的度为4,其余都是叶结点,问该树有几个叶结点?

在一个有限图中，各节点的度数总和是边数的2倍，而树中边数为节点数-1
设有x个叶子节点，先求出度数之和，d=2* 2 +1* 3 + 3*4+x；
d=19+x
顶点数：n = 2+1+3+x=6+x
边数: m=n-1 = 5+x
d=2m
19+x=10+2x
x=9
有9个叶节点

5. 一颗无向树T有5片树叶，3个2度分支点，其余的分支点都是3度顶点，问T有几个顶点

设其余3度顶点有x个
总度数d=5* 1 + 3* 2 + 3*x =11+3x
顶点数: n=5+3+x =8+x
对与无向树，边数: m=n-1 =7+x
d=2m
11+3x = 14+2x
x=3
顶点数为11

本人从事网路安全工作12年，曾在2个大厂工作过，安全服务、售后服务、售前、攻防比赛、安全讲师、销售经理等职位都做过，对这个行业了解比较全面。

最近遍览了各种网络安全类的文章，内容参差不齐，其中不伐有大佬倾力教学，也有各种不良机构浑水摸鱼，在收到几条私信，发现大家对一套完整的系统的网络安全从学习路线到学习资料，甚至是工具有着不小的需求。

最后，我将这部分内容融会贯通成了一套282G的网络安全资料包，所有类目条理清晰，知识点层层递进，需要的小伙伴可以点击下方小卡片领取哦！下面就开始进入正题，如何从一个萌新一步一步进入网络安全行业。

学习路线图

其中最为瞩目也是最为基础的就是网络安全学习路线图，这里我给大家分享一份打磨了3个月，已经更新到4.0版本的网络安全学习路线图。

相比起繁琐的文字，还是生动的视频教程更加适合零基础的同学们学习，这里也是整理了一份与上述学习路线一一对应的网络安全视频教程。

网络安全工具箱

当然，当你入门之后，仅仅是视频教程已经不能满足你的需求了，你肯定需要学习各种工具的使用以及大量的实战项目，这里也分享一份我自己整理的网络安全入门工具以及使用教程和实战。

项目实战

最后就是项目实战，这里带来的是SRC资料&HW资料，毕竟实战是检验真理的唯一标准嘛~

面试题

归根结底，我们的最终目的都是为了就业，所以这份结合了多位朋友的亲身经验打磨的面试题合集你绝对不能错过！