最新LeetCode 416

我们还可以这样写，二维数组`dp`是`boolean`类型，`dp[i][j]`表示数组中前`i`个元素的和是否可以组成和为`j`，很明显`dp[0][0]=true`，表示前`0`个元素（也就是没有元素）可以组成和为`0`。代码如下

public boolean canPartition(int[] nums) {
//计算数组中所有元素的和
int sum = 0;
for (int num : nums)
sum += num;
//如果sum是奇数，说明数组不可能分成完全相等的两份
if ((sum & 1) == 1)
return false;
//sum除以2
int target = sum >> 1;
int length = nums.length;
boolean[][]dp = new boolean[length + 1][target+1];
dp[0][0] = true;//base case
for (int i = 1; i <= length; i++) {
for (int j = 1; j <= target; j++) {
//递推公式
if (j >= nums[i - 1]) {
dp[i][j] = (dp[i - 1][j] || dp[i-1][j - nums[i - 1]]);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[length][target];
}

我们看到上面二维数组计算的时候当前值只和上面一行有关，所以我们可以把它改成一维的，注意第二个`for`循环要**倒叙**，否则会把前面的值给覆盖掉导致结果错误，仔细看一下  
 **dp[j] = (dp[j] || dp[j - nums[i - 1]]);**  
 就明白了，相当于同一行后面的值依赖前面的，如果不是倒叙，前面的值被修改了，在计算后面的就会导致错误。我们来看下代码。

public boolean canPartition(int[] nums) {
//计算数组中所有元素的和
int sum = 0;
for (int num : nums)
sum += num;
//如果sum是奇数，说明数组不可能分成完全相等的两份
if ((sum & 1) == 1)
return false;
//sum除以2
int target = sum >> 1;
int length = nums.length;
boolean[] dp = new boolean[target + 1];
dp[0] = true;//base case
for (int i = 1; i <= length; i++) {
//注意这里j要倒叙
for (int j = target; j >= 1; j–) {
//递推公式
if (j >= nums[i - 1]) {
dp[j] = (dp[j] || dp[j - nums[i - 1]]);
}
//else {//这里省略
// dp[j] = dp[j];
//}
}
}
return dp[target];
}

  

**DFS解决**


每种元素可以选择也可以不选择，只需要判断他所有的可能组合中，元素和是否有等于sum/2的，我们可以把它看做是一棵二叉树，左子节点表示选择当前元素，右子节点表示不选择当前元素，如下图所示，橙色节点表示选择当前元素，蓝色表示不选择。


![在这里插入图片描述](https://img-blog.csdnimg.cn/456f068c36ac41c1890f4ebae11b9a00.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5pWw5o2u57uT5p6E5ZKM566X5rOV,size_20,color_FFFFFF,t_70,g_se,x_16)  
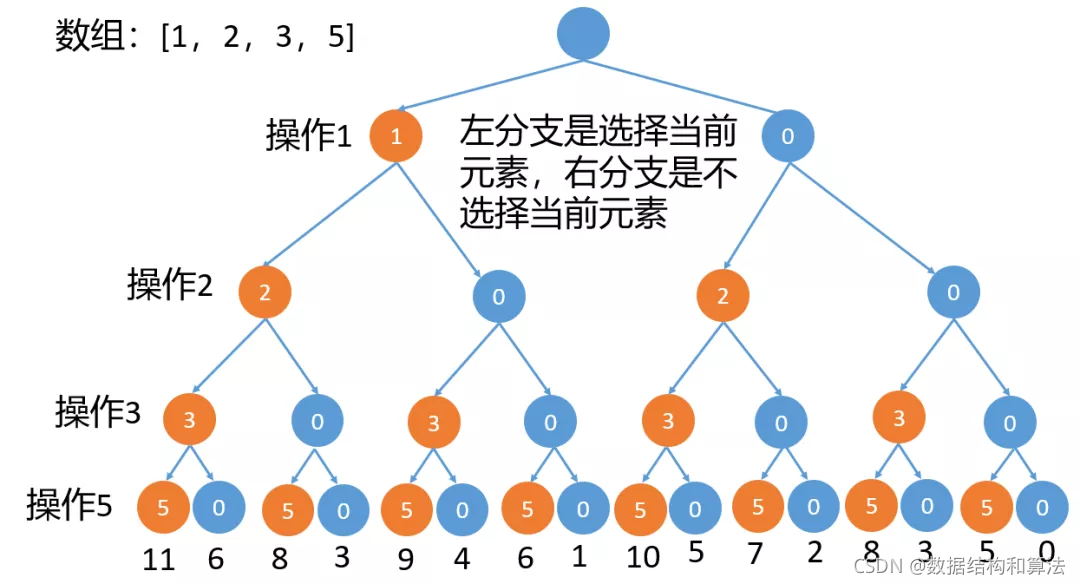
 我们来看下代码

public boolean canPartition(int[] nums) {
//计算数组中所有元素的和
int sum = 0;
for (int num : nums)
sum += num;
//如果sum是奇数，说明数组不可能分成完全相等的两份
if ((sum & 1) == 1)
return false;
return dfs(nums, sum >> 1, 0);
}

private boolean dfs(int[] nums, int target, int index) {
//targe等于0，说明存在一些元素的和等于sum/2，直接返回true
if (target == 0)
return true;
//如果数组元素都找完了，或者target小于0，直接返回false
if (index == nums.length || target < 0)
return false;
//选择当前元素和不选择当前元素两种情况
return dfs(nums, target - nums[index], index + 1)
|| dfs(nums, target, index + 1);
}

但很遗憾的是，因为计算量太大，会导致运行超时，我们可以优化一下，来看下代码

public boolean canPartition(int[] nums) {
//计算数组中所有元素的和
int sum = 0;
for (int num : nums)
sum += num;
//如果sum是奇数，说明数组不可能分成完全相等的两份
if ((sum & 1) == 1)
return false;
//sum除以2
int target = sum >> 1;
Boolean[][] map = new Boolean[nums.length][target + 1];
return dfs(nums, 0, target, map);
}

private boolean dfs(int[] nums, int index, int target, Boolean[][] map) {
//targe等于0，说明存在一些元素的和等于sum/2，直接返回true
if (target == 0)
return true;
//如果数组元素都找完了，或者target小于0，直接返回false
if (index == nums.length || target < 0)
return false;
//从map中取
if (map[index][target] != null)
return map[index][target];
//选择当前元素
boolean select = dfs(nums, index + 1, target - nums[index], map);
//不择当前元素
boolean unSelect = dfs(nums, index + 1, target, map);
//只要有一个为true，就返回true，否则返回false
if (select || unSelect) {
map[index][target] = true;
return true;
}
map[index][target] = false;
return false;
}

  

**位运算解决**


这里能使用位运算，关键在于题中的一些限制条件，比如


* **正整数的非空数组，**
* **每个数组中的元素不会超过 100，**
* **数组的大小不会超过 200等。**


原理很简单，我们只需要申请一个大小为`sum+1`的数组`bits[sum+1]`，数组中的数字只能是`0`和`1`，我们可以把它想象为一个**很长的二进制位**，因为`int`和`long`类型太短了，我们这里使用的是数组。然后每遍历数组中的一个元素比如`m`，就把二进制位往左移m位然后在和原来的二进制位进行或运算。最后判断`bits[sum/2]`是否是`1`，如果是`1`就返回`true`。文字叙述不是很直接，我们就以示例`1`为例来画个图看一下


![在这里插入图片描述](https://img-blog.csdnimg.cn/afe9d0e13daf4cd5bf0cdbb0b06b78a6.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5pWw5o2u57uT5p6E5ZKM566X5rOV,size_20,color_FFFFFF,t_70,g_se,x_16)  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/6dbdbd264da0412e9923d31ca4a16ddb.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5pWw5o2u57uT5p6E5ZKM566X5rOV,size_20,color_FFFFFF,t_70,g_se,x_16)  
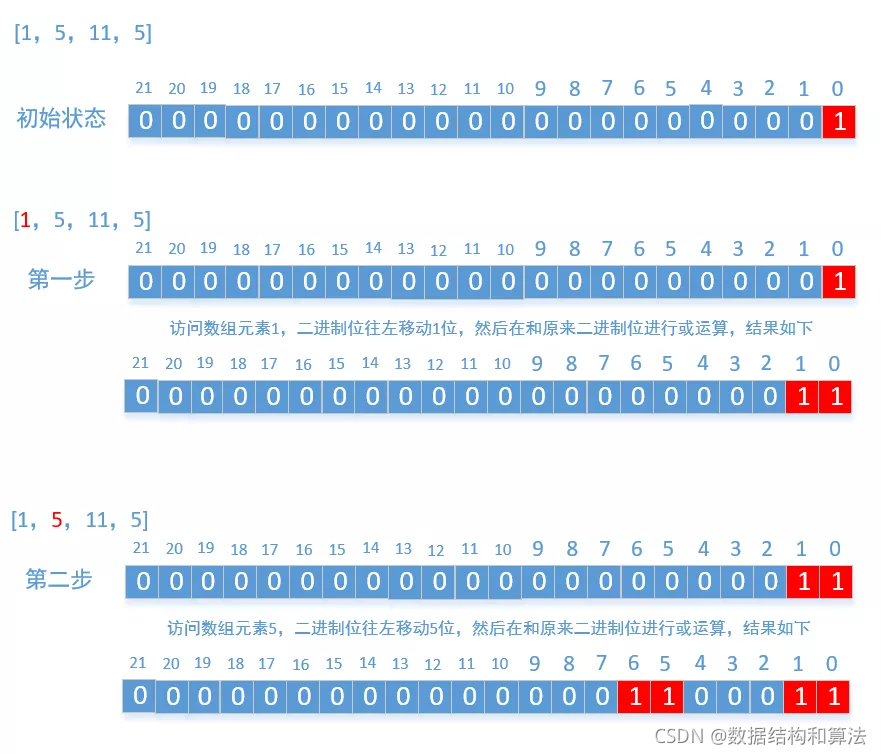
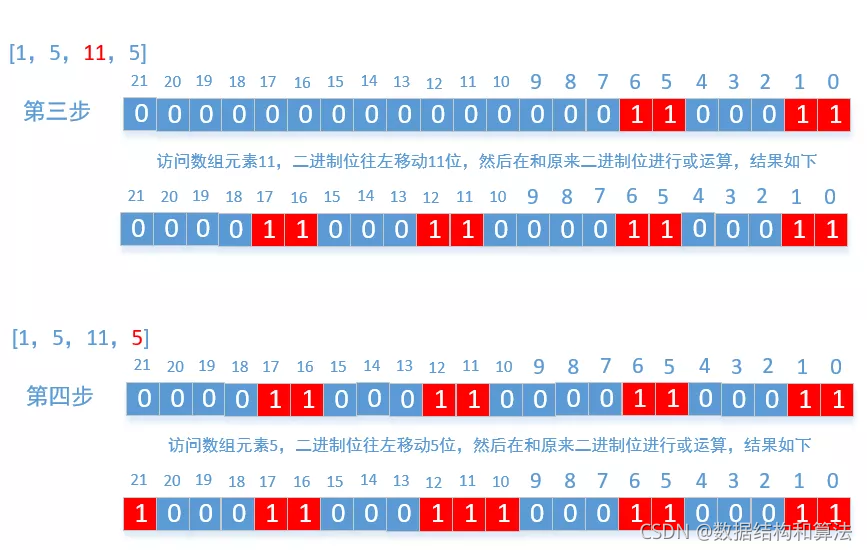
 最后你会发现一个规律，就是最后运算的结果**只要是1的位置，都可以使用数组中的元素组合而成，只要是0的都不能使用数组中的元素组合而成**，搞懂了上面的过程，代码就很容易写了。因为我们只需要判断二进制位中中间的那个值是否为1，所以我们只需要计算低位，高位完全不用计算，因为是往左移动的，高位不会对中间的值产生任何影响，所以这里能做一点优化，最后再来看下代码

public boolean canPartition(int[] nums) {
//计算数组中所有数字的和
int sum = 0;
for (int n : nums)
sum += n;
//如果sum是奇数，直接返回false
if ((sum & 1) == 1)
return false;
int len = sum >> 1;
//这里bits的长度是len+1，因为我们只需要计算

给大家的福利

零基础入门

对于从来没有接触过网络安全的同学，我们帮你准备了详细的学习成长路线图。可以说是最科学最系统的学习路线，大家跟着这个大的方向学习准没问题。

同时每个成长路线对应的板块都有配套的视频提供：

因篇幅有限，仅展示部分资料

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化资料的朋友，可以点击这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！