LeetCode 416

如果是偶数，我们只需要判断是否存在一些元素的和等于sum/2，如果等于sum/2，那么剩下的肯定也等于sum/2，说明我们可以把数组分为元素和相等的两部分。

那么这个时候问题就很明朗了，假设sum/2是一个背包的容量，我们只需要找出一些元素把他放到背包中，如果背包中元素的最大和等于sum/2，说明我们可以把数组分成完成相等的两份。这不就是经典的0-1背包问题吗。之前也讲过371，背包问题系列之-基础背包问题，具体可以看下，这里就不在重复介绍。我们在来找一下他的递推公式，定义dp[i][j]表示把第i个物品放到容量为j的背包中所获得的的最大值。

第i个物品的值是nums[i-1]：
如果nums[i-1]>j，说明背包容量不够，第i件物品放不进去，所以我们不能选择第i个物品，那么
dp[i][j]=dp[i-1][j]；

如果nums[i-1]<=j，说明可以把第j个物品放到背包中，我们可以选择放也可以选择不放，取最大值即可，如果放就会占用一部分背包容量，最大价值是

dp[i][j]=dp[i-1][j-nums[i-1]]+nums[i-1]

如果不放
dp[i][j]=dp[i-1][j]；
取两者的最大值

最终递推公式如下

if (j >= nums[i - 1]) {
    dp[i][j] = Math.max(dp[i - 1][j], dp[i-1][j - nums[i - 1]] + nums[i - 1]);
} else {
    dp[i][j] = dp[i - 1][j];
}

我们来看下最终代码

public boolean canPartition(int[] nums) {
    //计算数组中所有元素的和
    int sum = 0;
    for (int num : nums)
        sum += num;
    //如果sum是奇数，说明数组不可能分成完全相等的两份
    if ((sum & 1) == 1)
        return false;
    //sum除以2
    int target = sum >> 1;
    int length = nums.length;
    int[][] dp = new int[length + 1][target+1];
    for (int i = 1; i <= length; i++) {
        for (int j = 1; j <= target; j++) {
            //下面是递推公式
            if (j >= nums[i - 1]) {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i-1][j - nums[i - 1]] + nums[i - 1]);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    //判断背包最大是否能存放和为target的元素
    return dp[length][target] == target;
}

我们还可以这样写，二维数组dp是boolean类型，dp[i][j]表示数组中前i个元素的和是否可以组成和为j，很明显dp[0][0]=true，表示前0个元素（也就是没有元素）可以组成和为0。代码如下

public boolean canPartition(int[] nums) {
    //计算数组中所有元素的和
    int sum = 0;
    for (int num : nums)
        sum += num;
    //如果sum是奇数，说明数组不可能分成完全相等的两份
    if ((sum & 1) == 1)
        return false;
    //sum除以2
    int target = sum >> 1;
    int length = nums.length;
    boolean[][]dp = new boolean[length + 1][target+1];
    dp[0][0] = true;//base case
    for (int i = 1; i <= length; i++) {
        for (int j = 1; j <= target; j++) {
            //递推公式
            if (j >= nums[i - 1]) {
                dp[i][j] = (dp[i - 1][j] || dp[i-1][j - nums[i - 1]]);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[length][target];
}

我们看到上面二维数组计算的时候当前值只和上面一行有关，所以我们可以把它改成一维的，注意第二个for循环要倒叙，否则会把前面的值给覆盖掉导致结果错误，仔细看一下
dp[j] = (dp[j] || dp[j - nums[i - 1]]);
就明白了，相当于同一行后面的值依赖前面的，如果不是倒叙，前面的值被修改了，在计算后面的就会导致错误。我们来看下代码。

public boolean canPartition(int[] nums) {
    //计算数组中所有元素的和
    int sum = 0;
    for (int num : nums)
        sum += num;
    //如果sum是奇数，说明数组不可能分成完全相等的两份
    if ((sum & 1) == 1)
        return false;
    //sum除以2
    int target = sum >> 1;
    int length = nums.length;
    boolean[] dp = new boolean[target + 1];
    dp[0] = true;//base case
    for (int i = 1; i <= length; i++) {
        //注意这里j要倒叙
        for (int j = target; j >= 1; j--) {
            //递推公式
            if (j >= nums[i - 1]) {
                dp[j] = (dp[j] || dp[j - nums[i - 1]]);
            }
            //else {//这里省略
            // dp[j] = dp[j];
            //}
        }
    }
    return dp[target];
}

DFS解决

每种元素可以选择也可以不选择，只需要判断他所有的可能组合中，元素和是否有等于sum/2的，我们可以把它看做是一棵二叉树，左子节点表示选择当前元素，右子节点表示不选择当前元素，如下图所示，橙色节点表示选择当前元素，蓝色表示不选择。

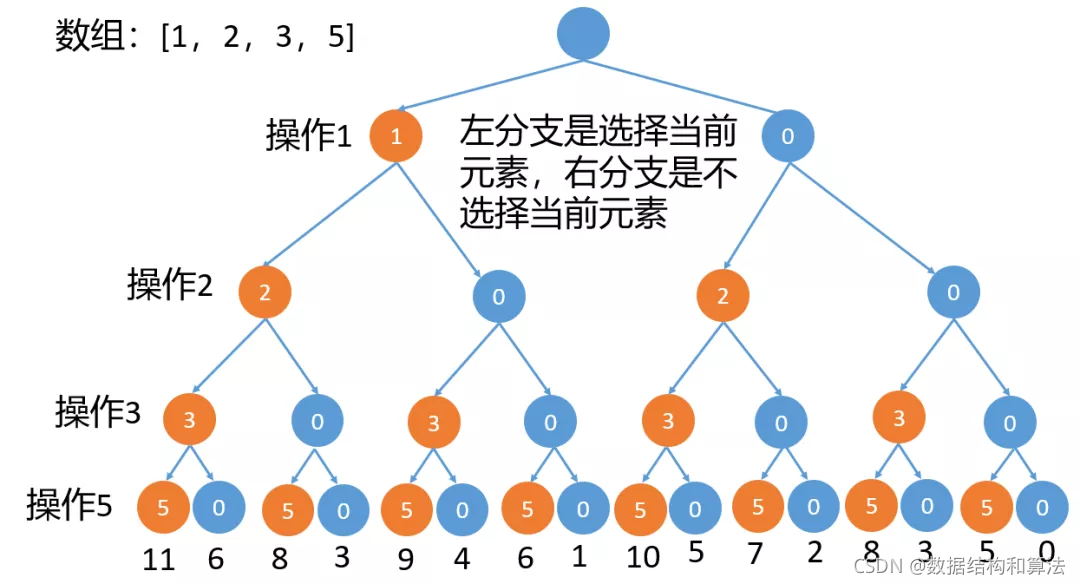
我们来看下代码

public boolean canPartition(int[] nums) {
    //计算数组中所有元素的和
    int sum = 0;
    for (int num : nums)
        sum += num;
    //如果sum是奇数，说明数组不可能分成完全相等的两份
    if ((sum & 1) == 1)
        return false;
    return dfs(nums, sum >> 1, 0);
}


private boolean dfs(int[] nums, int target, int index) {
    //targe等于0，说明存在一些元素的和等于sum/2，直接返回true
    if (target == 0)
        return true;
    //如果数组元素都找完了，或者target小于0，直接返回false
    if (index == nums.length || target < 0)
        return false;
    //选择当前元素和不选择当前元素两种情况
    return dfs(nums, target - nums[index], index + 1)
            || dfs(nums, target, index + 1);
}

但很遗憾的是，因为计算量太大，会导致运行超时，我们可以优化一下，来看下代码

还有兄弟不知道网络安全面试可以提前刷题吗？费时一周整理的160+网络安全面试题，金九银十，做网络安全面试里的显眼包！

王岚嵚工程师面试题（附答案），只能帮兄弟们到这儿了！如果你能答对70%，找一个安全工作，问题不大。

对于有1-3年工作经验，想要跳槽的朋友来说，也是很好的温习资料！

【完整版领取方式在文末！！】

93道网络安全面试题

内容实在太多，不一一截图了

黑客学习资源推荐

最后给大家分享一份全套的网络安全学习资料，给那些想学习 网络安全的小伙伴们一点帮助！

对于从来没有接触过网络安全的同学，我们帮你准备了详细的学习成长路线图。可以说是最科学最系统的学习路线，大家跟着这个大的方向学习准没问题。

😝朋友们如果有需要的话，可以联系领取~

1️⃣零基础入门

① 学习路线

对于从来没有接触过网络安全的同学，我们帮你准备了详细的学习成长路线图。可以说是最科学最系统的学习路线，大家跟着这个大的方向学习准没问题。

② 路线对应学习视频

同时每个成长路线对应的板块都有配套的视频提供：

2️⃣视频配套工具&国内外网安书籍、文档

① 工具

② 视频

③ 书籍

资源较为敏感，未展示全面，需要的最下面获取

② 简历模板

因篇幅有限，资料较为敏感仅展示部分资料，添加上方即可获取👆