本人从事网路安全工作12年,曾在2个大厂工作过,安全服务、售后服务、售前、攻防比赛、安全讲师、销售经理等职位都做过,对这个行业了解比较全面。
最近遍览了各种网络安全类的文章,内容参差不齐,其中不伐有大佬倾力教学,也有各种不良机构浑水摸鱼,在收到几条私信,发现大家对一套完整的系统的网络安全从学习路线到学习资料,甚至是工具有着不小的需求。
最后,我将这部分内容融会贯通成了一套282G的网络安全资料包,所有类目条理清晰,知识点层层递进,需要的小伙伴可以点击下方小卡片领取哦!下面就开始进入正题,如何从一个萌新一步一步进入网络安全行业。
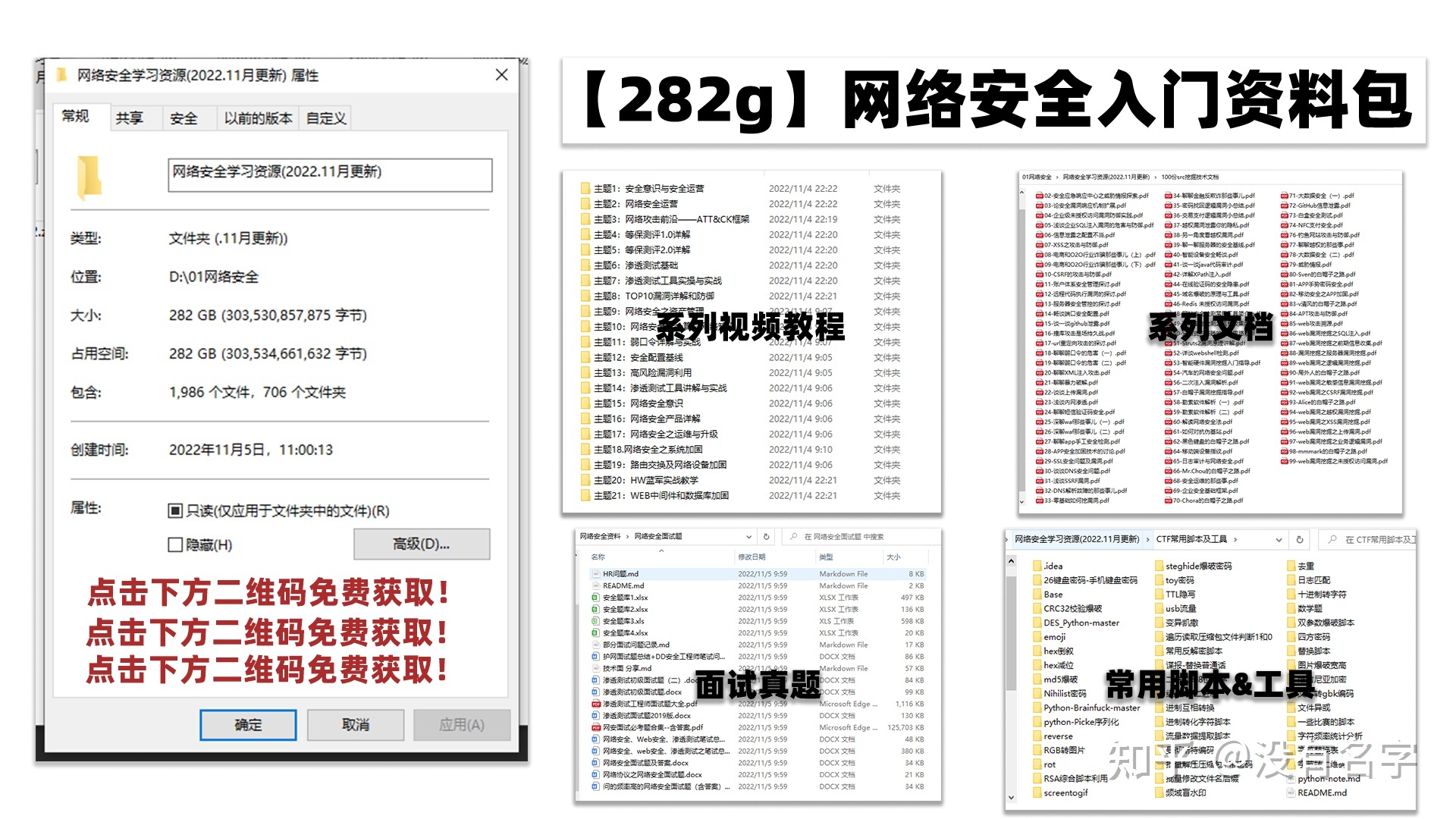
学习路线图
其中最为瞩目也是最为基础的就是网络安全学习路线图,这里我给大家分享一份打磨了3个月,已经更新到4.0版本的网络安全学习路线图。
相比起繁琐的文字,还是生动的视频教程更加适合零基础的同学们学习,这里也是整理了一份与上述学习路线一一对应的网络安全视频教程。
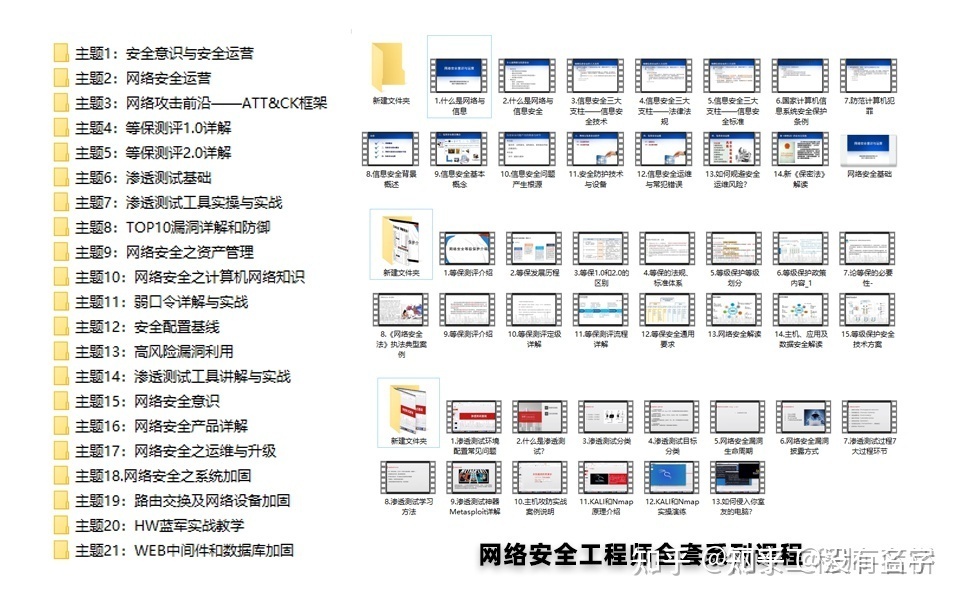
网络安全工具箱
当然,当你入门之后,仅仅是视频教程已经不能满足你的需求了,你肯定需要学习各种工具的使用以及大量的实战项目,这里也分享一份我自己整理的网络安全入门工具以及使用教程和实战。
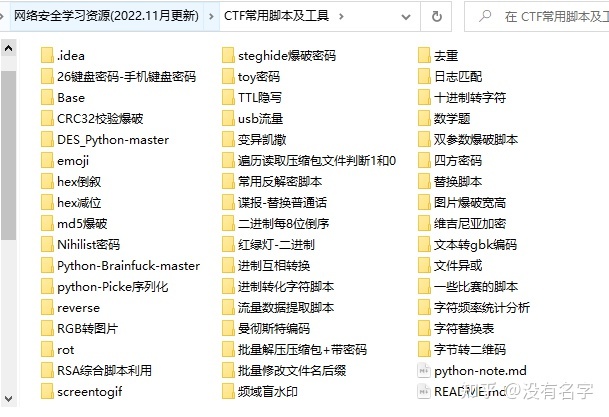
项目实战
最后就是项目实战,这里带来的是SRC资料&HW资料,毕竟实战是检验真理的唯一标准嘛~

面试题
归根结底,我们的最终目的都是为了就业,所以这份结合了多位朋友的亲身经验打磨的面试题合集你绝对不能错过!
网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!
Z
Z
Z的分布不可区分,
Y
Y
Y和
Z
Z
Z的分布不可区分,那么
X
X
X和
Y
Y
Y的分布是不可区分的吗?
-
语义安全(semantic security)
- 之前在导论部分有一个问题:如何定义不泄漏“meaningful”的信息。下面引入语义安全的概念来解决这个问题。
- 直觉:没有关于明文的任何有意义的信息泄漏
- 关于明文的信息用明文的函数来表示,
h
(
m
)
h(m)
h(m)表示敌手预先了解的关于明文的外部信息,
f
(
m
)
f(m)
f(m)表示敌手希望获取的关于明文的有意义的信息
- 定义:加密方案是窃听者出现时语义安全的,如果对于任意敌手,任意明文分布,任意函数
f
f
f和
h
h
h,一个敌手根据密文和
h
(
m
)
h(m)
h(m)获得
f
(
m
)
f(m)
f(m),另一个敌手只根据
h
(
m
)
h(m)
h(m)获得
f
(
m
)
f(m)
f(m),这两个敌手成功的概率之间的差异是可以忽略的
- 定理:一个私钥加密方案是窃听者不可区分的,当且仅当该方案是语义安全的。
- 证明略。直觉上,从右到左:若敌手能够在不可区分实验中成功(不是不可区分的),则意味着根据密文获得了关于区分明文的某些信息(不是语义安全);反之,若敌手能够获得关于明文的某些信息(不是语义安全),那么可以利用这些信息来区分明文(不是不可区分的)。
伪随机性
-
伪随机性概念(Pseudorandomness)
- 回顾之前完美保密的局限性,密钥长度需要和明文一样长才安全;计算安全中放松了安全的定义,那密钥能不能短一些,或者说能不能放松对随机性的要求,产生足够长但不完全随机的密钥?下面我们来学习伪随机性概念。
- 真随机性不能由一个可描述的机制产生。这里的“可描述的机制”显然是不包括“掷骰子”,而是指确定性的机制;
- 伪随机对于不知道其机制的观察者来说,看起来是真的随机;
- 一个固定的字符串谈不上是否随机/伪随机,随机/伪随机指的是产生字符串的过程;
- 问题:能否绝对地证明随机性?不能,因为我们可能是不知道其机制的观察者。
-
区分器(Distinguisher):统计测试
- 一类判断是否随机的务实的方法是,从一个随机生成器中得到多个随机序列并进行一套统计测试。
- 例如,序列中0和1的数量之差不应该太大,最大连续0的长度不应该太长等等。
- 伪随机性意味着下一比特不可预测(next-bit unpredictable),通过所有下一比特测试等且仅当通过所有统计测试。(这是姚期智的贡献)
- 问题是难以确定多少测试才足够?
-
定义伪随机性的直觉
- 直觉:从一个短的真随机种子生成一个长的随机串,这个伪随机串与真随机串是不可区分的。
- 这是不是和图灵测试类似?
- 区分器输入一个比特串,输出1位比特。注意:该比特不一定表示输入的串是否是随机的。
伪随机生成器(PRG)
-
伪随机生成器 (Pseudorandom Generator) 定义
- 一个确定性的多项式时间算法
G
:
{
0
,
1
}
n
→
{
0
,
1
}
ℓ
(
n
)
G : {0,1}^n \to {0,1}^{\ell(n)}
G:{0,1}n→{0,1}ℓ(n)是一个伪随机生成器(PRG),如果:
+ 延展:∀ n , ℓ ( n ) > n \forall n, \ell(n) > n ∀n,ℓ(n)>n。只有生成更长的串才有意义,否则可以直接从种子中复制一段输出; + 伪随机:对于任意PPT区分器 D D D, ∣ Pr [ D ( r ) = 1 ] − Pr [ D ( G ( s ) ) = 1 ] ∣ ≤ n e g l ( n ) \left|\Pr[D(r)=1] - \Pr[D(G(s))=1]\right| \le \mathsf{negl}(n) ∣Pr[D(r)=1]−Pr[D(G(s))=1]∣≤negl(n)。其中, r r r是随机的,种子 s s s随机的, ℓ ( ⋅ ) \ell(\cdot) ℓ(⋅)是延展因子。这里的意思是输出不同结果的概率差可以忽略,如果有一个区分器始终输出1,则两个概率都是1,差为0;另外,输出1并不需要表示特定含义,改成输出0也可以。- 存在性:若单向函数存在或
P
≠
N
P
\mathcal{P} \ne \mathcal{NP}
P=NP,则PRG存在。后面我们会进一步学习。
-
真实案例
- C语言的
random() - Netscape早期版本的漏洞https://people.eecs.berkeley.edu/~daw/papers/ddj-netscape.html
- C语言的
- 从这两个例子可以看出来,输出都是可预测的。
-
关于PRG的一些问题
- 利用下一比特不可预测,还有PRG的不可区分实验定义可以解决这些问题。
-
充分种子空间
- 稀疏输出:当扩展因子为
2
n
2n
2n时,在长度为
2
n
2n
2n的串中只会产生
2
−
n
2^{-n}
2−n。
- 蛮力攻击:给定无穷的时间,通过枚举所有种子来产生所有串,能以较高的概率区分出伪随机串。
- 充分种子空间:种子必须长来抵抗蛮力攻击。
-
不充分的随机性
- 2008年,为了避免一个编译警告,Debian的一个发布版本中误删了一行代码,引起OpenSSL中关于随机生成器的漏洞。
规约法
-
规约法(Reduction)
- 规约法是将一个问题A变换为另一个问题B。变换的意思可以理解为,A可以通过解决B来解决。
- 规约
A
≤
m
B
A \le_m B
A≤mB:
A
A
A可规约为B,如果B的解存在并且给定该解时A可解,其中
m
m
m表示映射规约;这里可以将规约理解为A对B的子函数调用,除了子函数B是一个黑盒,解决A的步骤都应该是明确的。
- 解决A不能比解决B更难,因为A可以通过解决B来得到解决。
- 例题,测量矩形面积可规约到测量矩形边长;计算一个数的平方可规约到两个数乘积,相反可以规约吗?
规约证明
-
规约证明
- 我们现在站在敌手的角色来思考,希望解决“破解”加密方案这个问题,并且在此之前我们已经知道有个一“假设”问题是不可解决的;
- 为了证明一个加密方案
Π
\Pi
Π在假设
X
X
X下是安全的,就是证明“破解”问题不可解。
- 将解决“假设”
X
X
X问题的算法
A
′
\mathcal{A}’
A′规约到“破解”
Π
\Pi
Π的算法
A
\mathcal{A}
A。如果加密方案可以被破解,则假设问题也可以解决。然而,由于假设问题是难以解决的,这导致矛盾,说明加密方案不可以被破解。
- 先令一个概率多项式时间的算法
A
\mathcal{A}
A能够以概率
ε
(
n
)
\varepsilon(n)
ε(n)破解
Π
\Pi
Π ;
- 假设:一个问题
X
X
X是难以解决的,即不存在多项式时间算法来解决
X
X
X;
A
′
\mathcal{A}’
A′是一个解决
X
X
X的概率算法;
- 规约:解决假设问题
X
X
X可以通过破解加密方案
Π
\Pi
Π,即将
A
′
\mathcal{A}’
A′规约到
A
\mathcal{A}
A,
A
′
\mathcal{A}’
A′通过以
A
\mathcal{A}
A作为子函数可以以概率
1
/
p
(
n
)
1/p(n)
1/p(n)有效地解决问题
X
X
X;
- 矛盾:若加密方案可以被有效破解,即
ε
(
n
)
\varepsilon(n)
ε(n)是不可忽略的,则
A
′
\mathcal{A}’
A′可以以不可忽略的概率
ε
(
n
)
/
p
(
n
)
\varepsilon(n)/p(n)
ε(n)/p(n)解决问题
X
X
X,这与假设矛盾,因而
ε
(
n
)
\varepsilon(n)
ε(n)一定是可忽略的。
-
一个规约法证明PRG的例子
- 假设
F
F
F是PRG,证明
G
G
G也是PRG。
- 问题A:如何区分
F
F
F;问题B:如何区分
G
G
G;
- 从A规约到B:区分
F
F
F的算法输入按位取反后作为区分
G
G
G的算法输入,区分
G
G
G的算法输出作为区分
F
F
F的算法输出。
-
一个规约法证明PRG的例子(续)
- 由此,建立了不可区分定义中概率的联系。
构造安全的加密方案
-
一个安全的定长加密方案
- ∣
G
(
k
)
∣
=
ℓ
(
∣
k
∣
)
|G(k)| = \ell(|k|)
∣G(k)∣=ℓ(∣k∣),
m
∈
{
0
,
1
}
ℓ
(
n
)
m \in {0,1}^{\ell(n)}
m∈{0,1}ℓ(n), 一个PRG以长度为
n
n
n的密钥作为种子,输出与明文相同长度的pad;
- G
e
n
\mathsf{Gen}
Gen:
k
∈
{
0
,
1
}
n
k \in {0,1}^n
k∈{0,1}n,密钥作为种子,长度小于明文长度;
- E
n
c
\mathsf{Enc}
Enc:
c
:
=
G
(
k
)
⊕
m
c := G(k)\oplus m
c:=G(k)⊕m,加密方法和一次一密一样;
- D
e
c
\mathsf{Dec}
Dec:
m
:
=
G
(
k
)
⊕
c
m := G(k)\oplus c
m:=G(k)⊕c,解密也是;
- 定理:该定长加密方案是窃听下不可区分的。
- 直觉上,这个方案和一次一密是类似的,除了密钥更短并且用伪随机生成器生成的比特串来与明文异或。因为伪随机对于任何敌手都可以认为是真随机,所以对于敌手而言,该方案与一次一密是一样的。由此,我们得到了一个安全的加密方案,同时避免了一次一密的最大局限性——密钥过长。
-
证明不可区分加密方案
- 思路:区分伪随机性为难题假设,破解加密方案为规约的子函数。针对伪随机生成器
G
G
G的区分器
D
D
D以
A
\mathcal{A}
A为子函数,使得当
A
\mathcal{A}
A破解了
Π
\Pi
Π则
D
D
D可以区分出
G
G
G,与
G
G
G的伪随机性矛盾。注意这里我们用了符号
Π
~
\tilde{\Pi}
Π~来表示
Π
\Pi
Π的一个变体,来刻画加密方案中可能使用了真随机串来加密;
- 回顾针对伪随机生成器的区分器
D
D
D的问题是,输入一个串
w
w
w,输出一个比特;这里关键问题是输出的比特从何而来?
- 将
D
D
D规约到
A
\mathcal{A}
A。回顾窃听者不可区分实验中,
A
\mathcal{A}
A与一个挑战者进行3轮交互:
1. A\mathcal{A} A选择两个不同明文 m 0 , m 1 m\_0, m\_1 m0,m1,并发送给挑战者; 2. 挑战者生成密钥,并随机挑选一个明文 m b m\_b mb加密后得到挑战密文 c c c,并发送给 A \mathcal{A} A; 3. A \mathcal{A} A输出对所加密明文的猜测 b ′ b' b′,若 b = b ′ b=b' b=b′,则 A \mathcal{A} A成功;否则,失败;- 区分器
D
D
D成为窃听不可区分实验中的挑战者,特别之处在于:在第2步,不需要生成密钥,而是直接以输入串
w
w
w作为pad来加密,
c
:
=
w
⊕
m
b
c := w \oplus m_b
c:=w⊕mb;根据
w
w
w的两种可能,分两种情况:
+ 当w w w是由 G G G生成的,即伪随机串,则 c c c就是加密方案 Π \Pi Π中密文, A \mathcal{A} A面对的就是 Π \Pi Π; + 当 w w w是真随机串,则 c c c不同于加密方案 Π \Pi Π中密文,而与一次一密中一样, A \mathcal{A} A面对的就是 Π ~ \tilde{\Pi} Π~一次一密;- 回答前面关于
D
D
D输出什么的问题:破解加密方案的
A
\mathcal{A}
A成功时,
D
D
D输出1;否则,
D
D
D输出0。
-
证明不可区分加密方案(续)
- 规约完毕,证明
A
\mathcal{A}
A在实验中成功的概率是可忽略的
+ 当w w w为真随机串 r r r,就是一次一密, Pr [ D ( r )
写在最后
在结束之际,我想重申的是,学习并非如攀登险峻高峰,而是如滴水穿石般的持久累积。尤其当我们步入工作岗位之后,持之以恒的学习变得愈发不易,如同在茫茫大海中独自划舟,稍有松懈便可能被巨浪吞噬。然而,对于我们程序员而言,学习是生存之本,是我们在激烈市场竞争中立于不败之地的关键。一旦停止学习,我们便如同逆水行舟,不进则退,终将被时代的洪流所淘汰。因此,不断汲取新知识,不仅是对自己的提升,更是对自己的一份珍贵投资。让我们不断磨砺自己,与时代共同进步,书写属于我们的辉煌篇章。
需要完整版PDF学习资源私我
网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!






















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








