先自我介绍一下,小编浙江大学毕业,去过华为、字节跳动等大厂,目前阿里P7
深知大多数程序员,想要提升技能,往往是自己摸索成长,但自己不成体系的自学效果低效又漫长,而且极易碰到天花板技术停滞不前!
因此收集整理了一份《2024年最新网络安全全套学习资料》,初衷也很简单,就是希望能够帮助到想自学提升又不知道该从何学起的朋友。



既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上网络安全知识点,真正体系化!
由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新
如果你需要这些资料,可以添加V获取:vip204888 (备注网络安全)

正文
适用条件
加权连通图(可以判定图是否连通)
测试所用图
与
所用图相同,就是课本上的。
算法步骤
1.对边按权重排序为e1、e2、…
2.若已选择V-1条边,停止。否则,按边的权重排序选择下一条边。
3.判断选择的边的两点是否在同一连通分支。若不在同一分支,则选择该边。返回步骤2。
Kruskal算法代码
//最小生成树-Kruskal算法
void Kruskal(Graph G)
{
//初始化
sort(l.begin(), l.end(),cmp);
int verSet[MaxVerNum];
int mincost = 0;
for (int i = 0; i < G.vexnum; i++)
verSet[i] = i;
cout << "最小生成树所有边:" << endl;
//依次查看边
int all = 0;
for (int i = 0; i < G.arcnum; i++)
{
if (all == G.vexnum - 1)break;
int v1 = verSet[l[i].from];
int v2 = verSet[l[i].to];
//该边连接两个连通分支
if (v1 != v2)
{
cout << "(" << l[i].from << "," << l[i].to << ") ";
mincost += l[i].weight;
//合并连通分支
for (int j = 0; j < G.vexnum; j++)
{
if (verSet[j] == v2)verSet[j] = v1;
}
all++;
}
}
cout << "最小生成树权值之和:" <<mincost<<endl;
}
全部代码
/*
Project: 图-最小生成树-Kruskal算法
Date: 2019/11/10
Author: Frank Yu
基本操作函数:
InitGraph(Graph &G) 初始化函数 参数:图G 作用:初始化图的顶点表,邻接矩阵等
InsertNode(Graph &G,VexType v) 插入点函数 参数:图G,顶点v 作用:在图G中插入顶点v,即改变顶点表
InsertEdge(Graph &G,VexType v,VexType w) 插入边函数 参数:图G,某边两端点v和w 作用:在图G两点v,w之间加入边,即改变邻接矩阵
Adjancent(Graph G,VexType v,VexType w) 判断是否存在边(v,w)函数 参数:图G,某边两端点v和w 作用:判断是否存在边(v,w)
BFS(Graph G, int start) 广度遍历函数 参数:图G,开始结点下标start 作用:宽度遍历
DFS(Graph G, int start) 深度遍历函数(递归形式)参数:图G,开始结点下标start 作用:深度遍历
Dijkstra(Graph G, int v) 最短路径 - Dijkstra算法 参数:图G、源点v
功能实现函数:
CreateGraph(Graph &G) 创建图功能实现函数 参数:图G InsertNode 作用:创建图
BFSTraverse(Graph G) 广度遍历功能实现函数 参数:图G 作用:宽度遍历
DFSTraverse(Graph G) 深度遍历功能实现函数 参数:图G 作用:深度遍历
Shortest_Dijkstra(Graph &G) 调用最短路径-Dijkstra算法 参数:图G、源点v
Prim(Graph G) 最小生成树-Prim算法 参数:图G
Kruskal(Graph G) 最小生成树-Kruskal算法 参数:图G
*/
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<string>
#include<set>
#include<list>
#include<queue>
#include<vector>
#include<map>
#include<iterator>
#include<algorithm>
#include<iostream>
#define MaxVerNum 100 //顶点最大数目值
#define VexType char //顶点数据类型
#define EdgeType int //边数据类型,无向图时邻接矩阵对称,有权值时表示权值,没有时1连0不连
#define INF 0x3f3f3f3f//作为最大值
using namespace std;
//图的数据结构
typedef struct Graph
{
VexType Vex[MaxVerNum];//顶点表
EdgeType Edge[MaxVerNum][MaxVerNum];//边表
int vexnum, arcnum;//顶点数、边数
}Graph;
//迪杰斯特拉算法全局变量
bool S[MaxVerNum]; //顶点集
int D[MaxVerNum]; //到各个顶点的最短路径
int Pr[MaxVerNum]; //记录前驱
//Prim算法所用数据结构
typedef struct closedge
{
int adjvex; //最小边在集合U(最小边在当前子树顶点集合中的那个顶点的下标)
int lowcost; //最小边上的权值
};
//Kruskal算法所用数据结构
typedef struct Edge
{
int from; //起点下标
int to; //终点下标
int weight; //权值
};
vector<Edge> l;
//按权值比较
bool cmp(Edge e1, Edge e2)
{
if (e1.weight<e2.weight)
{
return true;
}
return false;
}
//*********************************************基本操作函数*****************************************//
//初始化函数 参数:图G 作用:初始化图的顶点表,邻接矩阵等
void InitGraph(Graph &G)
{
memset(G.Vex, '#', sizeof(G.Vex));//初始化顶点表
//初始化边表
for (int i = 0; i < MaxVerNum; i++)
for (int j = 0; j < MaxVerNum; j++)
{
G.Edge[i][j] = INF;
if (i == j)G.Edge[i][j] = 0;//在最小生成树时,考虑无环简单图,故自己到自己设置为0
}
G.arcnum = G.vexnum = 0; //初始化顶点数、边数
}
//插入点函数 参数:图G,顶点v 作用:在图G中插入顶点v,即改变顶点表
bool InsertNode(Graph &G, VexType v)
{
if (G.vexnum < MaxVerNum)
{
G.Vex[G.vexnum++] = v;
return true;
}
return false;
}
//插入边函数 参数:图G,某边两端点v和w 作用:在图G两点v,w之间加入边,即改变邻接矩阵
bool InsertEdge(Graph &G, VexType v, VexType w, int weight)
{
int p1, p2;//v,w两点下标
p1 = p2 = -1;//初始化
for (int i = 0; i<G.vexnum; i++)//寻找顶点下标
{
if (G.Vex[i] == v)p1 = i;
if (G.Vex[i] == w)p2 = i;
}
if (-1 != p1&&-1 != p2)//两点均可在图中找到
{
G.Edge[p1][p2] = G.Edge[p2][p1] = weight;//无向图邻接矩阵对称
G.arcnum++;
//Kruskal算法增加代码
Edge e;
e.from = p1;
e.to = p2;
e.weight = weight;
l.push_back(e);
return true;
}
return false;
}
//判断是否存在边(v,w)函数 参数:图G,某边两端点v和w 作用:判断是否存在边(v,w)
bool Adjancent(Graph G, VexType v, VexType w)
{
int p1, p2;//v,w两点下标
p1 = p2 = -1;//初始化
for (int i = 0; i<G.vexnum; i++)//寻找顶点下标
{
if (G.Vex[i] == v)p1 = i;
if (G.Vex[i] == w)p2 = i;
}
if (-1 != p1&&-1 != p2)//两点均可在图中找到
{
if (G.Edge[p1][p2] == 1)//存在边
{
return true;
}
return false;
}
return false;
}
bool visited[MaxVerNum];//访问标记数组,用于遍历时的标记
//广度遍历函数 参数:图G,开始结点下标start 作用:宽度遍历
void BFS(Graph G, int start)
{
queue<int> Q;//辅助队列
cout << G.Vex[start];//访问结点
visited[start] = true;
Q.push(start);//入队
while (!Q.empty())//队列非空
{
int v = Q.front();//得到队头元素
Q.pop();//出队
for (int j = 0; j<G.vexnum; j++)//邻接点
{
if (G.Edge[v][j] <INF && !visited[j])//是邻接点且未访问
{
cout << "->";
cout << G.Vex[j];//访问结点
visited[j] = true;
Q.push(j);//入队
}
}
}//while
cout << endl;
}
//深度遍历函数(递归形式)参数:图G,开始结点下标start 作用:深度遍历
void DFS(Graph G, int start)
{
cout << G.Vex[start];//访问
visited[start] = true;
for (int j = 0; j < G.vexnum; j++)
{
if (G.Edge[start][j] < INF && !visited[j])//是邻接点且未访问
{
cout << "->";
DFS(G, j);//递归深度遍历
}
}
}
//最短路径 - Dijkstra算法 参数:图G、源点v
void Dijkstra(Graph G, int v)
{
//初始化
int n = G.vexnum;//n为图的顶点个数
for (int i = 0; i < n; i++)
{
S[i] = false;
D[i] = G.Edge[v][i];
if (D[i] < INF)Pr[i] = v; //v与i连接,v为前驱
else Pr[i] = -1;
}
S[v] = true;
D[v] = 0;
//初始化结束,求最短路径,并加入S集
for (int i = 1; i < n; i++)
{
int min = INF;
int temp;
for (int w = 0; w < n; w++)
if (!S[w] && D[w] < min) //某点temp未加入s集,且为当前最短路径
{
temp = w;
min = D[w];
}
S[temp] = true;
//更新从源点出发至其余点的最短路径 通过temp
for (int w = 0; w < n; w++)
if (!S[w] && D[temp] + G.Edge[temp][w] < D[w])
{
D[w] = D[temp] + G.Edge[temp][w];
Pr[w] = temp;
}
}
}
//输出最短路径
void Path(Graph G, int v)
{
if (Pr[v] == -1)
return;
Path(G, Pr[v]);
cout << G.Vex[Pr[v]] << "->";
}
//**********************************************功能实现函数*****************************************//
//打印图的顶点表
void PrintVex(Graph G)
{
for (int i = 0; i < G.vexnum; i++)
{
cout << G.Vex[i] << " ";
}
cout << endl;
}
//打印图的边矩阵
void PrintEdge(Graph G)
{
for (int i = 0; i < G.vexnum; i++)
{
for (int j = 0; j < G.vexnum; j++)
{
if (G.Edge[i][j] == INF)cout << "∞ ";
else cout << G.Edge[i][j] << " ";
}
cout << endl;
}
}
//创建图功能实现函数 参数:图G InsertNode 作用:创建图
void CreateGraph(Graph &G)
{
VexType v, w;
int vn, an;//顶点数,边数
cout << "请输入顶点数目:" << endl;
cin >> vn;
cout << "请输入边数目:" << endl;
cin >> an;
cout << "请输入所有顶点名称:" << endl;
for (int i = 0; i<vn; i++)
{
cin >> v;
if (InsertNode(G, v)) continue;//插入点
else {
cout << "输入错误!" << endl; break;
}
}
还有兄弟不知道网络安全面试可以提前刷题吗?费时一周整理的160+网络安全面试题,金九银十,做网络安全面试里的显眼包!
王岚嵚工程师面试题(附答案),只能帮兄弟们到这儿了!如果你能答对70%,找一个安全工作,问题不大。
对于有1-3年工作经验,想要跳槽的朋友来说,也是很好的温习资料!
【完整版领取方式在文末!!】
***93道网络安全面试题***
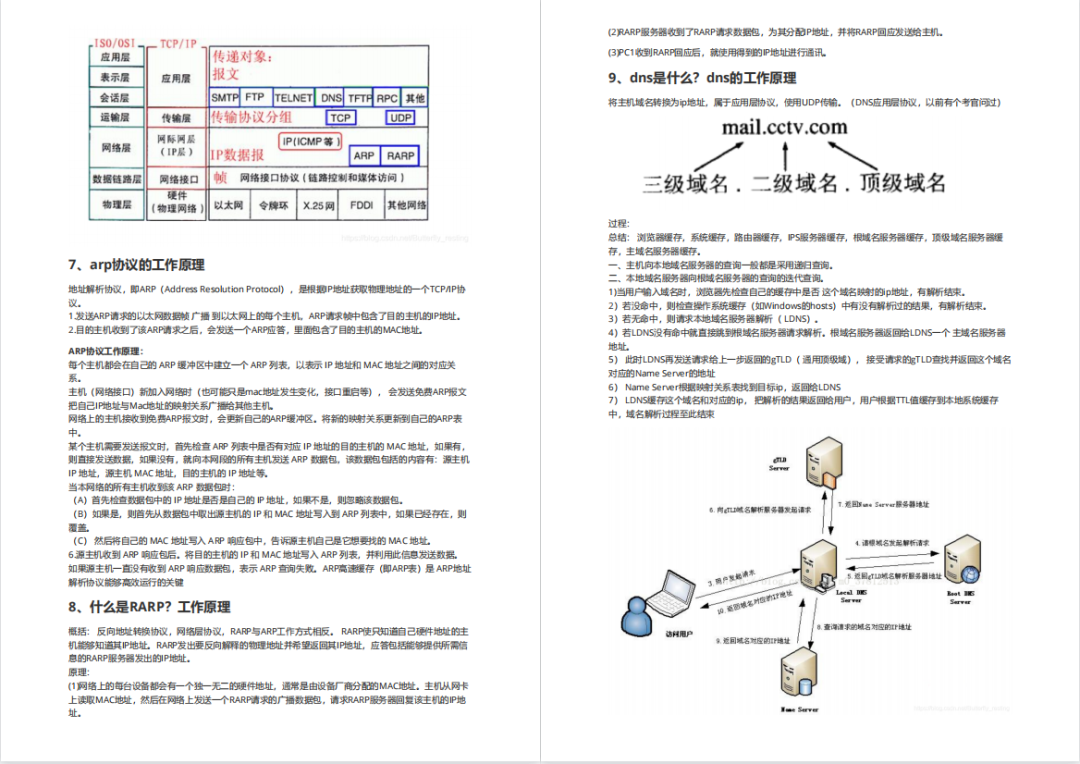


内容实在太多,不一一截图了
### 黑客学习资源推荐
最后给大家分享一份全套的网络安全学习资料,给那些想学习 网络安全的小伙伴们一点帮助!
对于从来没有接触过网络安全的同学,我们帮你准备了详细的学习成长路线图。可以说是最科学最系统的学习路线,大家跟着这个大的方向学习准没问题。
😝朋友们如果有需要的话,可以联系领取~
#### 1️⃣零基础入门
##### ① 学习路线
对于从来没有接触过网络安全的同学,我们帮你准备了详细的**学习成长路线图**。可以说是**最科学最系统的学习路线**,大家跟着这个大的方向学习准没问题。
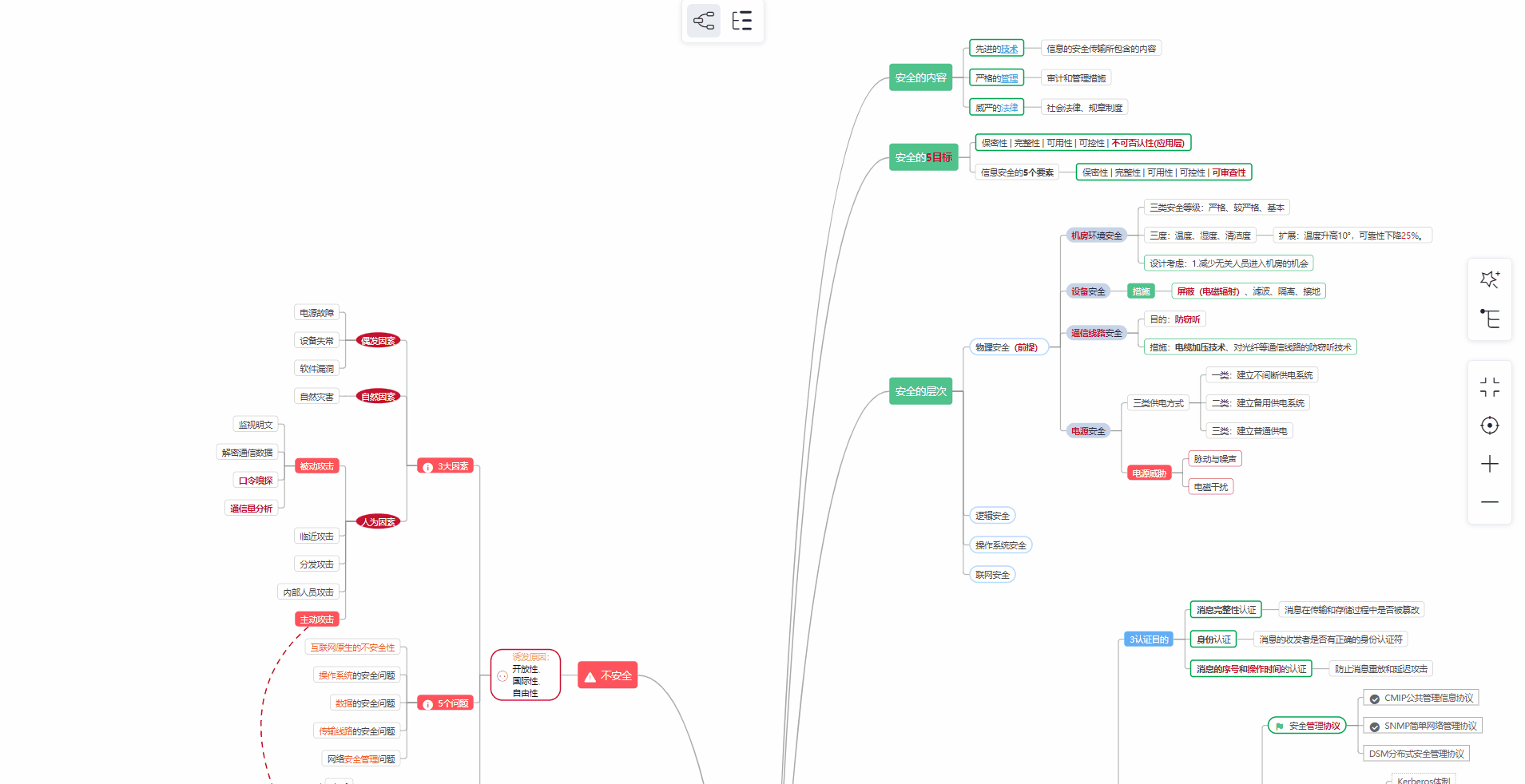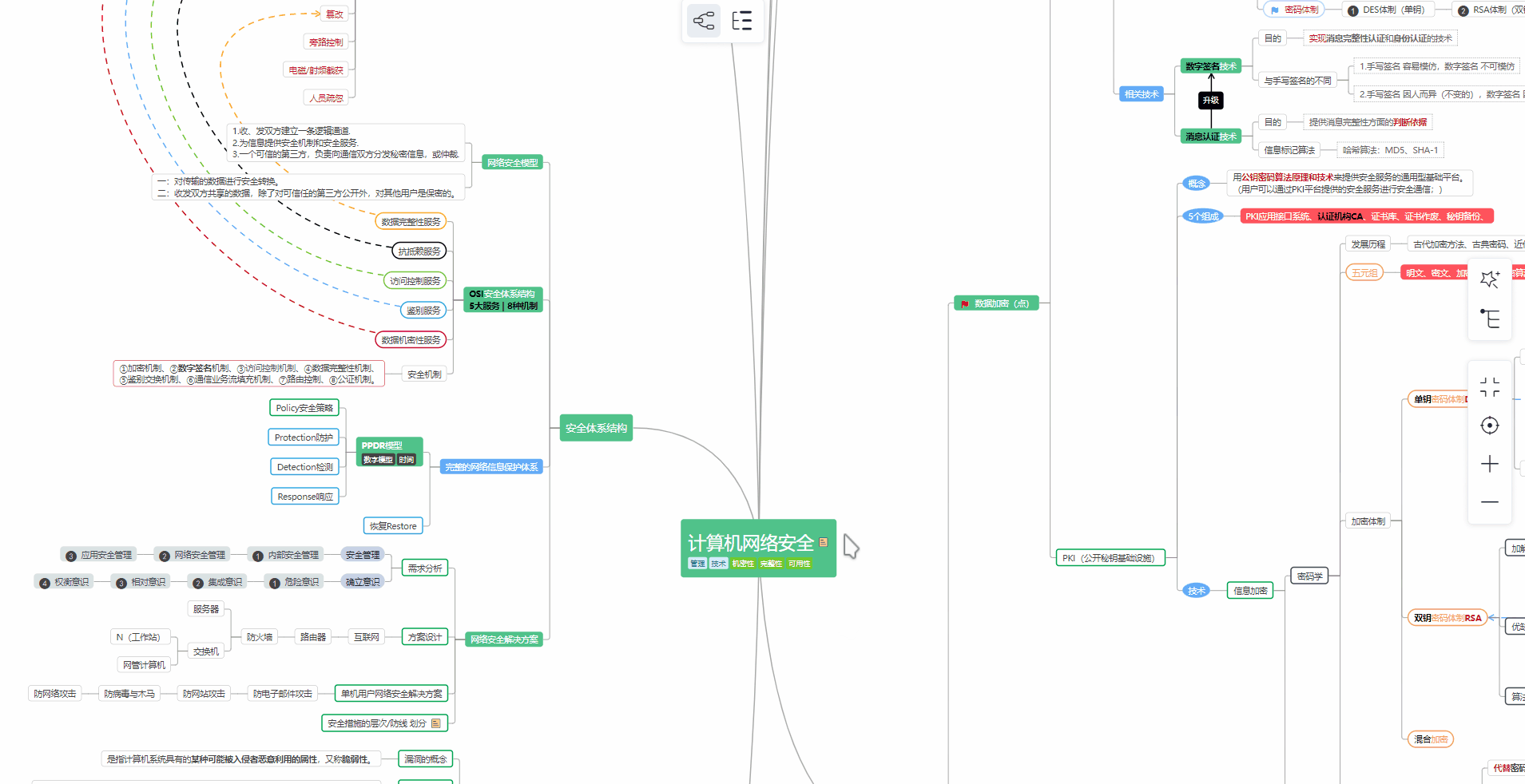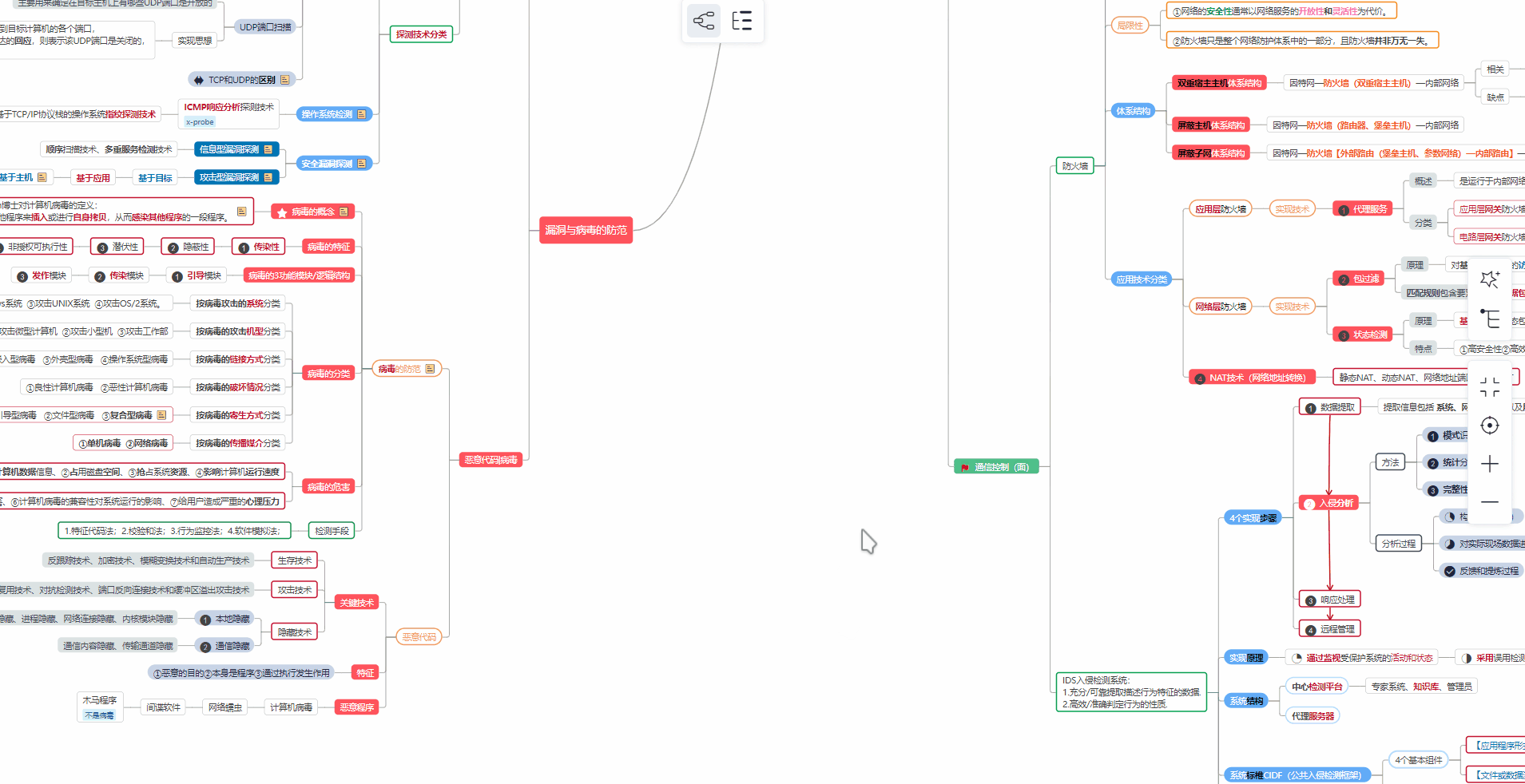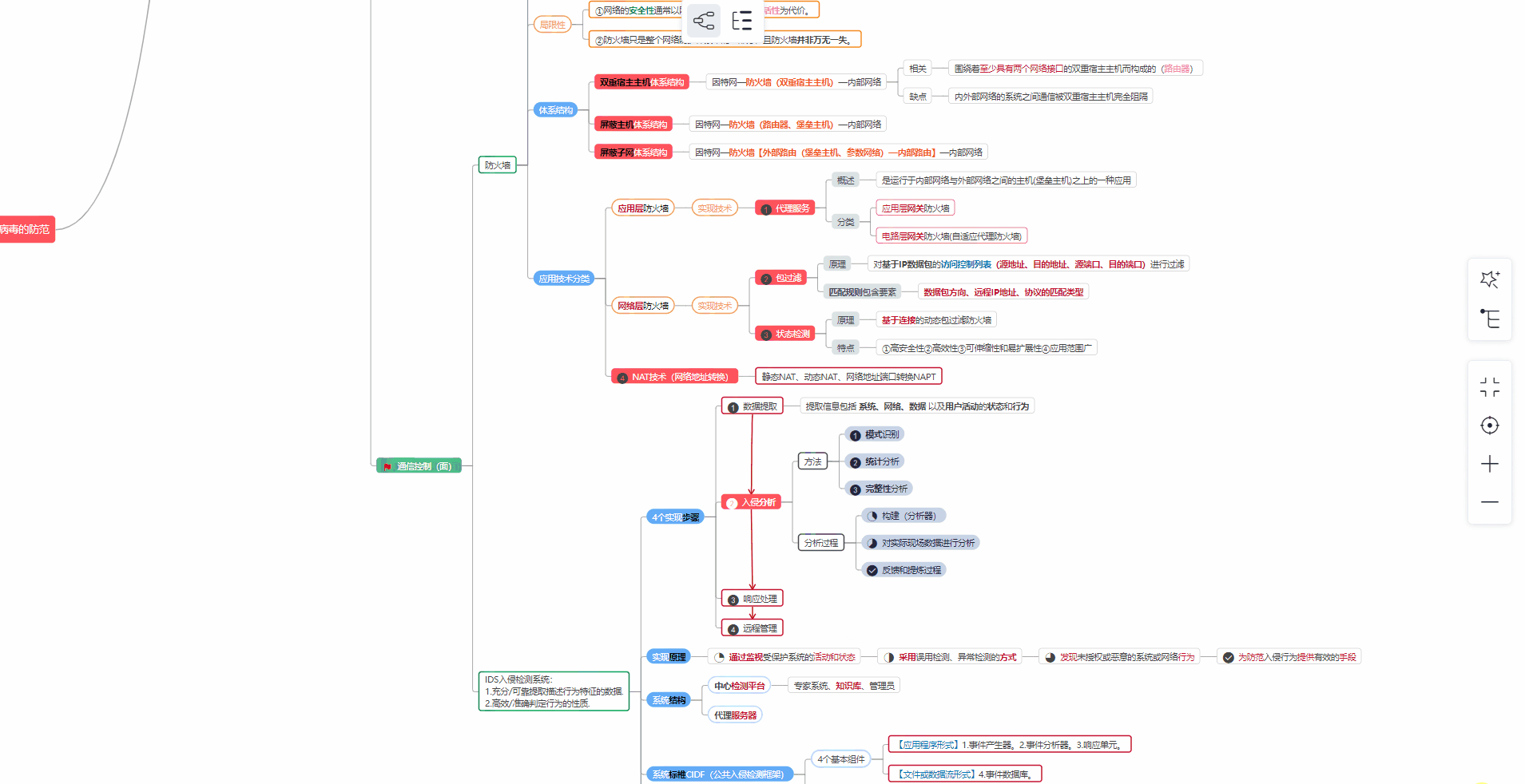
##### ② 路线对应学习视频
同时每个成长路线对应的板块都有配套的视频提供:

#### 2️⃣视频配套工具&国内外网安书籍、文档
##### ① 工具

##### ② 视频
##### ③ 书籍
资源较为敏感,未展示全面,需要的最下面获取
##### ② 简历模板
**因篇幅有限,资料较为敏感仅展示部分资料,添加上方即可获取👆**
**网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**
**需要这份系统化的资料的朋友,可以添加V获取:vip204888 (备注网络安全)**

**一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!**
.csdnimg.cn/111f5462e7df433b981dc2430bb9ad39.png#pic_center)
##### ② 简历模板

**因篇幅有限,资料较为敏感仅展示部分资料,添加上方即可获取👆**
**网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**
**需要这份系统化的资料的朋友,可以添加V获取:vip204888 (备注网络安全)**
[外链图片转存中...(img-iyTiqpO6-1713374168879)]
**一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!**
























 4323
4323

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








