您可能感兴趣的文章推荐
前言
很多人加我都是想询问如何学好算法。我的方法是我用了 十年 的时间，自己总结出来的，不可能适合所有人，但是我觉得挺有效的，如果你觉得可行，尽管一试！
首先，我们心中要有一团🔥火🔥，一团希望之🔥火🔥！只要你心中充满希望，即使是死去的意志也会在你内心复活。
你永远无法弥补你的过去，但是，你可以改变你的未来！就算暗淡无光的尘土，也会有爆发光芒的那一刻！抓住那尘埃中的刹那光辉，燃烧自己吧！**「 动态规划 」**作为算法中一块比较野的内容，没有比较系统的分类，只能通过不断总结归纳，对各种类型进行归类。
「 动态规划 」（即
Dynamic programming，简称 DP）是一种在数学、管理科学、计算机科学 以及 生物信息学中使用的，通过把原问题分解为相对简单的
**「 子问题 」**的方式求解
**「 复杂问题 」**的方法。**「 动态规划 」**是一种算法思想：若要解一个给定问题，我们需要解其不同部分（即
「 子问题 」），再根据
**「 子问题 」**的解以得出原问题的解。要理解动态规划，就要理解
「 最优子结构 」 和
「 重复子问题 」。本文将针对以下一些常用的动态规划问题，进行由浅入深的系统性讲解。首先来看一个简单的分类，也是今天本文要讲的内容。
点击我跳转末尾 获取 粉丝专属 《算法和数据结构》源码，以及获取博主的联系方式。
文章目录
一、递推问题
递推问题作为动态规划的基础，是最好掌握的，也是必须掌握的，它有点类似于高中数学中的数列，通过 前几项的值 推导出 当前项的值。
1、一维递推
你正在爬楼梯，需要
n
n
n 阶你才能到达楼顶。每次你可以爬
1
1
1 或
2
2
2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
假设我们已经到了第
n
n
n 阶楼梯，那么它可以是从
n
−
1
n-1
n−1 阶过来的，也可以是从
n
−
2
n-2
n−2 阶过来的（但是，不可能是从
n
−
3
n-3
n−3 阶直接过来的），所以如果达到第
n
n
n 阶的方案数为
f
[
n
]
f[n]
f[n]，那么到达
n
−
1
n-1
n−1 阶就是
f
[
n
−
1
]
f[n-1]
f[n−1]，到达
n
−
2
n-2
n−2 阶 就是
f
[
n
−
2
]
f[n-2]
f[n−2]，所以可以得出：
f
[
n
]
=
f
[
n
−
1
]
f
[
n
−
2
]
f[n] = f[n-1] + f[n-2]
f[n]=f[n−1]+f[n−2] 其中，当
n
=
0
n=0
n=0 时方案数为 1，代表初始情况；
n
=
1
n=1
n=1 时方案数为 1，代表走了一步，递推计算即可。
以上就是最简单的动态规划问题，也是一个经典的数列：斐波那契数列 的求解方式。它通过一个递推公式，将原本指数级的问题转化成了线性的，时间复杂度为
O
(
n
)
O(n)
O(n)。
C语言代码实现如下：
int f[1000];
int climbStairs(int n){
f[0] = f[1] = 1;
for(int i = 2; i <= n; ++i) {
f[i] = f[i-1] + f[i-2];
}
return f[n];
}
2、二维递推
给定一个非负整数
n
n
n，生成杨辉三角的前
n
n
n 行。在杨辉三角中，每个数是它 左上方 和 右上方 的数的和。
根据杨辉三角的定义，我们可以简单将上面的图进行一个变形，得到：
于是，我们可以得出以下结论：
1）杨辉三角的所有数可以存储在一个二维数组中，行代表第一维，列代表第二维度；
2）第
i
i
i 行的元素个数为
i
i
i 个；
3）第
i
i
i 行 第
j
j
j 列的元素满足公式：
c
[
i
]
[
j
]
=
{
1
i
=
0
c
[
i
−
1
]
[
j
−
1
]
c
[
i
−
1
]
[
j
]
o
t
h
e
r
w
i
s
e
c[i][j] = \begin{cases} 1 & i=0\ c[i-1][j-1] + c[i-1][j] & otherwise \end{cases}
c[i][j]={1c[i−1][j−1]+c[i−1][j]i=0otherwise
于是就可以两层循环枚举了。时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)。
C语言代码实现如下：
int c[40];
void generate(int n) {
for(int i = 0; i < n; ++i) {
for(int j = 0; j <= i; ++j) {
if(j == 0 || j == i) {
c[i][j] = 1;
}else {
c[i][j] = c[i-1][j-1] + c[i-1][j];
}
}
}
}
二、线性DP
1、最小花费
数组的每个下标作为一个阶梯，第
i
i
i 个阶梯对应着一个非负数的体力花费值
c
o
s
t
[
i
]
cost[i]
cost[i]（下标从 0 开始）。每当爬上一个阶梯，都要花费对应的体力值，一旦支付了相应的体力值，就可以选择 向上爬一个阶梯 或者 爬两个阶梯。求找出达到楼层顶部的最低花费。在开始时，可以选择从下标为
0
0
0 或
1
1
1 的元素作为初始阶梯。
令走到第
i
i
i 层的最小消耗为
f
[
i
]
f[i]
f[i]。假设当前的位置在
i
i
i 层楼梯，那么只可能从
i
−
1
i-1
i−1 层过来，或者
i
−
2
i-2
i−2 层过来；
如果从
i
−
1
i-1
i−1 层过来，则需要消耗体力值：
f
[
i
−
1
]
c
o
s
t
[
i
−
1
]
f[i-1] + cost[i-1]
f[i−1]+cost[i−1]；
如果从
i
−
2
i-2
i−2 层过来，则需要消耗体力值：
f
[
i
−
2
]
c
o
s
t
[
i
−
2
]
f[i-2] + cost[i-2]
f[i−2]+cost[i−2]；
起点可以在第 0 或者 第 1 层，于是有状态转移方程：
f
[
i
]
=
{
0
i
=
0
,
1
min
(
f
[
i
−
1
]
c
o
s
t
[
i
−
1
]
,
f
[
i
−
2
]
c
o
s
t
[
i
−
2
]
)
i
1
f[i] = \begin{cases} 0 & i=0,1\ \min ( f[i-1] + cost[i-1], f[i-2] + cost[i-2] ) & i > 1\end{cases}
f[i]={0min(f[i−1]+cost[i−1],f[i−2]+cost[i−2])i=0,1i>1
这个问题和一开始的递推问题的区别在于：一个是求前两项的和，一个是求最小值。这里就涉及到了动态取舍的问题，也就是动态规划的思想。
如果从前往后思考，每次都有两种选择，时间复杂度为
O
(
2
n
)
O(2^n)
O(2n)。转化成动态规划以后，只需要一个循环，时间复杂度为
O
(
n
)
O(n)
O(n)。
C语言代码实现如下：
int f[1024];
int min(int a, int b) {
return a < b ? a : b;
}
int minCostClimbingStairs(int\* cost, int costSize){
f[0] = 0;
f[1] = 0;
for(int i = 2; i <= costSize; ++i) {
f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2]);
}
return f[costSize];
}
2、最大子段和
给定一个整数数组
n
u
m
s
nums
nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
由于要求的是连续的子数组，所以对于第
i
i
i 个元素，状态转移一定是从
i
−
1
i-1
i−1 个元素转移过来的。基于这一点，可以令
f
[
i
]
f[i]
f[i] 表示以
i
i
i 号元素结尾的最大值。
那么很自然，这个最大值必然包含
n
u
m
s
[
i
]
nums[i]
nums[i] 这个元素，那么要不要包含
n
u
m
s
[
i
−
1
]
,
n
u
m
s
[
i
−
2
]
,
n
u
m
s
[
i
−
3
]
,
.
.
.
,
n
u
m
s
[
k
]
nums[i-1],nums[i-2],nums[i-3],…,nums[k]
nums[i−1],nums[i−2],nums[i−3],…,nums[k] 呢？其实就是看第
i
−
1
i-1
i−1 号元素结尾的最大值是否大于零，也就是：当
f
[
i
−
1
]
≤
0
f[i-1] \le 0
f[i−1]≤0 时，则 前
i
−
1
i-1
i−1 个元素是没必要包含进来的。所以就有状态转移方程：
f
[
i
]
=
{
n
u
m
s
[
0
]
i
=
0
n
u
m
s
[
i
]
f
[
i
−
1
]
≤
0
n
u
m
s
[
i
]
f
[
i
−
1
]
f
[
i
−
1
]
0
f[i] = \begin{cases} nums[0] & i = 0 \ nums[i] & f[i-1] \le 0 \ nums[i] + f[i-1] & f[i-1] > 0\end{cases}
f[i]=⎩⎪⎨⎪⎧nums[0]nums[i]nums[i]+f[i−1]i=0f[i−1]≤0f[i−1]>0一层循环枚举后，取
m
a
x
(
f
[
i
]
)
max(f[i])
max(f[i]) 就是答案了。只需要一个循环，时间复杂度为
O
(
n
)
O(n)
O(n)。
C语言代码实现如下：
int dp[30010];
int max(int a, int b) {
return a > b ? a : b;
}
int maxSubArray(int\* nums, int numsSize){
int maxValue = nums[0];
dp[0] = nums[0];
for(int i = 1; i < numsSize; ++i) {
dp[i] = nums[i];
if(dp[i-1] > 0) {
dp[i] += dp[i-1];
}
maxValue = max(maxValue, dp[i]);
}
return maxValue;
}
3、最长单调子序列
给定一个长度为
n
(
1
≤
n
≤
1000
)
n(1 \le n \le 1000)
n(1≤n≤1000) 的数组
a
i
a_i
ai，求给出它的最长递增子序列的长度。
在看这个问题之前，我们先来明确一些概念：单调序列、单调子序列、最大长单调子序列。
单调序列 就是一个满足某种单调性的数组序列，比如 单调递增序列、单调递减序列、单调不增序列、单调不减序列。举几个简单的例子：
单调递增序列：1，2，3，7，9
单调递减序列：9，8，4，2，1
单调不增序列：9，8，8，5，2
单调不减序列：1，2，2，5，5
一个比较直观的单调递增序列的例子就是一个楼梯的侧面。
我们可以把这个楼梯每一阶的高度用一个数字表示，得到一个单调递增序列，如图所示：
单调子序列 指的是任意一个数组序列，按顺序选择一些元素组成一个新的序列，并且满足单调性。对于一个长度为
n
n
n 的序列，每个元素可以选择 “取” 或者 “不取”，所以最多情况下，有
2
n
2^n
2n 个单调子序列。
如图所示，代表的是序列：[1，2，4，6，3，5，9]
其中 [1，2，6] 为它的一个长度为 3 的单调子序列，如图所示；
[1，3，6] 则不是，因为 3 和 6 的顺序不是原序列中的顺序；[1，4，3] 也不是，因为它不满足单调性。
最长单调子序列 是指对于原数组序列，能够找到的元素个数最多的单调子序列。
还是以 [1，2，4，6，3，5，9] 为例，它的最长单调子序列为：[1，2，4，6，9]，长度为 5；
当然，也可以是 [1，2，3，5，9]，长度同样为 5。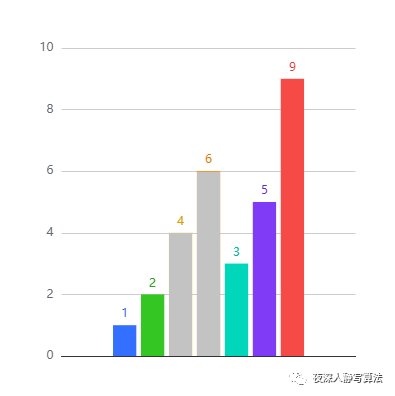
那么，接下来，我们看下如何通过动态规划的方法来求解 最长递增子序列。
对于数组序列
a
i
(
1
≤
i
≤
n
)
a_i(1 \le i \le n)
ai(1≤i≤n)，令
f
[
i
]
f[i]
f[i] 表示以第
i
i
i 个数
a
i
a_i
ai 结尾的最长递增子序列的长度。那么，我们考虑以第
i
i
i 个数
a
i
a_i
ai 结尾的最长递增子序列，它在这个序列中的前一个数一定是
a
j
(
1
≤
j
<
i
)
a_j(1 \le j < i)
aj(1≤j<i) 中的一个，所以，如果我们已经知道了
f
[
j
]
f[j]
f[j]，那么就有
f
[
i
]
=
f
[
j
]
1
f[i] = f[j] + 1
f[i]=f[j]+1。显然，我们还需要满足
a
j
<
a
i
a_j < a_i
aj<ai 这个递增的限制条件。
那么就可以得出状态转移方程：
f
[
i
]
=
max
j
=
1
i
−
1
(
f
[
j
]
∣
a
j
<
a
i
)
1
f[i] = \max_{j=1}^{i-1} (f[j] \ | \ a_j < a_i) + 1
f[i]=j=1maxi−1(f[j] ∣ aj<ai)+1 这里
f
[
j
]
f[j]
f[j] 是
f
[
i
]
f[i]
f[i] 的子结构，而
m
a
x
(
f
[
j
]
)
max(f[j])
max(f[j]) 是
f
[
i
]
f[i]
f[i] 的最优子结构，当然我们需要考虑一种情况，就是没有找到最优子结构的时候，例如：
i
=
1
i=1
i=1 或者 不存在
a
j
<
a
i
a_j < a_i
aj<ai 的
j
j
j，此时
f
[
i
]
=
1
f[i] = 1
f[i]=1，表示
a
i
a_i
ai 本身是一个长度为
1
1
1 的最长递增子序列。
f
[
i
]
f[i]
f[i] 数组可以通过两层循环来求解，如下图表所示：
状态数
f
[
.
.
.
]
f[…]
f[…] 总共
O
(
n
)
O(n)
O(n) 个，状态转移的消耗为
O
(
n
)
O(n)
O(n)，所以总的时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)，所以对于这类问题，一般能够接受的
n
n
n 的范围在千级别，也就是
1000
,
2000
,
3000…
1000, 2000, 3000 …
1000,2000,3000…。如果是
n
=
10000
,
100000
n=10000, 100000
n=10000,100000 的情况，就需要考虑优化了。
有关最长单调子序列的问题，还有
O
(
n
l
o
g
2
n
)
O(nlog_2n)
O(nlog2n) 的优化算法，具体方法可以参考以下文章：夜深人静写算法（二十）- 最长单调子序列。
三、二维DP
1、最长公共子序列
给定两个数组序列
a
1
,
a
2
,
.
.
.
,
a
n
a_1, a_2, …, a_n
a1,a2,…,an 和
b
1
,
b
2
,
.
.
.
,
b
m
b_1, b_2, …, b_m
b1,b2,…,bm，其中
n
,
m
≤
1000
n,m \le 1000
n,m≤1000，求两个数组的最长公共子序列。
考虑两个数组序列
a
1
,
a
2
,
.
.
.
,
a
n
a_1, a_2, …, a_n
a1,a2,…,an 和
b
1
,
b
2
,
.
.
.
,
b
m
b_1, b_2, …, b_m
b1,b2,…,bm，对于
a
a
a 序列中第
i
i
i 个元素
a
i
a_i
ai 和
b
b
b 序列中的第
j
j
j 个元素
b
j
b_j
bj，有两种情况：
(
1
)
(1)
(1) 相等即
a
i
=
=
b
j
a_i == b_j
ai==bj 的情况，这个时候如果前缀序列
a
1
,
a
2
,
.
.
.
,
a
i
−
1
a_1, a_2, …, a_{i-1}
a1,a2,…,ai−1 和
b
1
,
b
2
,
.
.
.
,
b
j
−
1
b_1, b_2, …, b_{j-1}
b1,b2,…,bj−1 的最长公共子序列已经求出来了，记为
x
x
x 的话，那么很显然，在两个序列分别加入
a
i
a_i
ai 和
b
j
b_j
bj 以后，长度又贡献了 1，所以
a
1
,
a
2
,
.
.
.
,
a
i
a_1, a_2, …, a_{i}
a1,a2,…,ai 和
b
1
,
b
2
,
.
.
.
,
b
j
b_1, b_2, …, b_{j}
b1,b2,…,bj 的最长公共子序列就是
x
1
x+1
x+1；
(
2
)
(2)
(2) 不相等即
a
i
≠
b
j
a_i \neq b_j
ai=bj 的情况，这个时候我们可以把问题拆分成两个更小的子问题，即 分别去掉
a
i
a_i
ai 和
b
j
b_j
bj 的情况，如图所示：
去掉
a
i
a_i
ai 以后，问题转变为求：
a
1
,
a
2
,
.
.
.
,
a
i
−
1
a_1, a_2, …, a_{i-1}
a1,a2,…,ai−1 和
b
1
,
b
2
,
.
.
.
,
b
j
b_1, b_2, …, b_{j}
b1,b2,…,bj 的最长公共子序列；
去掉
b
j
b_j
bj 以后，问题转变为求：
a
1
,
a
2
,
.
.
.
,
a
i
a_1, a_2, …, a_{i}
a1,a2,…,ai 和
b
1
,
b
2
,
.
.
.
,
b
j
−
1
b_1, b_2, …, b_{j-1}
b1,b2,…,bj−1 的最长公共子序列；
根据上面的两种情况的讨论，我们发现，在任何时候，我们都在求
a
a
a 的前缀 和
b
b
b 的前缀的最长公共序列，所以可以这么定义状态：用
f
[
i
]
[
j
]
f[i][j]
f[i][j] 表示
a
1
,
a
2
,
.
.
.
,
a
i
a_1, a_2, …, a_{i}
a1,a2,…,ai 和
b
1
,
b
2
,
.
.
.
,
b
j
b_1, b_2, …, b_{j}
b1,b2,…,bj 的最长公共子序列。
在设计状态的过程中，我们已经无形中把状态转移也设计好了，状态转移方程如下：
f
[
i
]
[
j
]
=
{
0
i
=
0
o
r
j
=
0
f
[
i
−
1
]
[
j
−
1
]
1
i
,
j
0
,
a
i
=
b
j
max
(
f
[
i
]
[
j
−
1
]
,
f
[
i
−
1
]
[
j
]
)
i
,
j
0
,
a
i
≠
b
j
f[i][j] = \begin{cases}0 & i=0\ or\ j=0 \ f[i-1][j-1] + 1 & i,j>0,a_i=b_j \ \max(f[i][j-1], f[i-1][j]) & i,j>0,a_i \neq b_j\end{cases}
f[i][j]=⎩⎪⎨⎪⎧0f[i−1][j−1]+1max(f[i][j−1],f[i−1][j])i=0 or j=0i,j>0,ai=bji,j>0,ai=bj 对于
i
=
0
i=0
i=0 或者
j
=
0
j=0
j=0 代表的是：其中一个序列的长度为 0，那么最长公共子序列的长度肯定就是 0 了；
其余两种情况，就是我们上文提到的
a
i
a_i
ai 和
b
j
b_j
bj “相等” 与 “不相等” 的两种情况下的状态转移。如图所示，代表了字符串 “GATCGTGAGC” 和 “AGTACG” 求解最长公共子序列的
f
[
i
]
[
j
]
(
i
,
j
0
)
f[i][j] (i,j > 0)
f[i]j 的矩阵。
对于长度分别为
n
n
n 和
m
m
m 的两个序列，求解它们的最长公共子序列时，状态数总共有
O
(
n
m
)
O(nm)
O(nm) 个，每次状态转移的消耗为
O
(
1
)
O(1)
O(1)，所以总的时间复杂度为
O
(
n
m
)
O(nm)
O(nm)。
对于
f
[
i
]
[
j
]
f[i][j]
f[i][j] 这个状态，求解过程中，只依赖于
f
[
i
]
[
j
−
1
]
f[i][j-1]
f[i][j−1]、
f
[
i
−
1
]
[
j
−
1
]
f[i-1][j-1]
f[i−1][j−1]、
f
[
i
−
1
]
[
j
]
f[i-1][j]
f[i−1][j]。
即每次求解只需要有 上一行 和 这一行 的状态即可，所以可以采用滚动数组进行优化，将状态转移方程变成：
f
[
c
u
r
]
[
j
]
=
{
f
[
l
a
s
t
]
[
j
−
1
]
1
j
0
,
a
i
=
b
j
max
(
f
[
c
u
r
]
[
j
−
1
]
,
f
[
l
a
s
t
]
[
j
]
)
j
0
,
a
i
≠
b
j
f[cur][j] = \begin{cases}f[last][j-1] + 1 & j>0,a_i=b_j \ \max(f[cur][j-1], f[last][j]) & j>0,a_i \neq b_j\end{cases}
f[cur][j]={f[last][j−1]+1max(f[cur][j−1],f[last][j])j>0,ai=bjj>0,ai=bj 只需要简单将
i
i
i 替换成
c
u
r
cur
cur，
i
−
1
i-1
i−1 替换成
l
a
s
t
last
last 即可。这样就把原本
O
(
n
m
)
O(nm)
O(nm) 的空间复杂度变成了
O
(
p
)
O§
O§，其中
p
=
min
(
n
,
m
)
p = \min(n,m)
p=min(n,m)。
- 优化后的 C++ 代码实现如下：
typedef char ValueType;
const int maxn = 5010;
int f[2][maxn];
int getLCSLength(int hsize, ValueType \*h, int vsize, ValueType \*v) {
memset(f, 0, sizeof(f));
int cur = 1, last = 0;
for (int i = 1; i <= vsize; ++i) {
for (int j = 1; j <= hsize; ++j) {
if (v[i] == h[j])
f[cur][j] = f[last][j - 1] + 1;
else
f[cur][j] = max(f[cur][j - 1], f[last][j]);
}
swap(last, cur);
}
return f[last][hsize];
}
有关于 最长公共子序列 的更多内容，可以参考以下内容：夜深人静写算法（二十一）- 最长公共子序列。
2、最小编辑距离
长度为
n
n
n 的源字符串
a
1
,
a
2
,
.
.
.
,
a
n
a_1,a_2,…,a_n
a1,a2,…,an，经过一些给定操作变成长度为
m
m
m 的目标字符串
b
1
,
b
2
,
.
.
.
b
m
b_1,b_2,…b_m
b1,b2,…bm，操作包括如下三种：
1）I
n
s
e
r
t
Insert
Insert：在源字符串中插入一个字符，插入消耗为
I
I
I；
2）D
e
l
e
t
e
Delete
Delete：在源字符串中删除一个字符，删除消耗为
D
D
D；
3）R
e
p
l
a
c
e
Replace
Replace：将源字符串中的一个字符替换成另一个字符，替换消耗为
R
R
R；
求最少的总消耗，其中n
,
m
≤
1000
n,m \le 1000
n,m≤1000。
令
f
[
i
]
[
j
]
f[i][j]
f[i][j] 表示源字符串
a
1
,
a
2
,
.
.
.
,
a
i
a_1,a_2,…,a_i
a1,a2,…,ai 经过上述三种操作变成目标字符串
b
1
,
b
2
,
.
.
.
b
j
b_1,b_2,…b_j
b1,b2,…bj 的最少消耗。
假设
a
1
,
a
2
,
.
.
.
,
a
i
a_1,a_2,…,a_{i}
a1,a2,…,ai 变成
b
1
,
b
2
,
.
.
.
b
j
−
1
b_1,b_2,…b_{j-1}
b1,b2,…bj−1 的最少消耗已经求出，等于
f
[
i
]
[
j
−
1
]
f[i][j-1]
f[i][j−1]，则需要在
a
[
i
]
a[i]
a[i] 的后面插入一个字符
b
j
b_j
bj，那么产生的消耗为：
f
[
i
]
[
j
−
1
]
I
f[i][j-1] + I
f[i][j−1]+I 如图所示，源字符串为 “AGTA”，目标字符串为 “GATCGT” 的情况下，将源字符串变成 "“GATCG” 的最小消耗为
f
[
i
]
[
j
−
1
]
f[i][j-1]
f[i][j−1]，那么只要在源字符串最后再插入一个 ‘T’，就可以把源字符串变成目标字符串 “GATCGT”；
假设
a
1
,
a
2
,
.
.
.
,
a
i
−
1
a_1,a_2,…,a_{i-1}
a1,a2,…,ai−1 变成
b
1
,
b
2
,
.
.
.
b
j
b_1,b_2,…b_{j}
b1,b2,…bj 的最少消耗已经求出，等于
f
[
i
−
1
]
[
j
]
f[i-1][j]
f[i−1][j]，则需要把
a
i
a_i
ai 个删掉，那么产生的消耗为：
f
[
i
−
1
]
[
j
]
D
f[i-1][j] + D
f[i−1][j]+D 如图所示，源字符串为 “AGTA”，目标字符串为 “GATCGT” 的情况下，将 “AGT” 变成目标字符串的最小消耗为
f
[
i
−
1
]
[
j
]
f[i-1][j]
f[i−1][j]，那么只要把源字符串最后一个’A’删掉，就可以把源字符串变成目标字符串；
假设
a
1
,
a
2
,
.
.
.
,
a
i
−
1
a_1,a_2,…,a_{i-1}
a1,a2,…,ai−1 变成
b
1
,
b
2
,
.
.
.
b
j
−
1
b_1,b_2,…b_{j-1}
b1,b2,…bj−1 的最少消耗已经求出，等于
f
[
i
−
1
]
[
j
−
1
]
f[i-1][j-1]
f[i−1][j−1]，则将
a
i
a_i
ai 替换成
b
j
b_j
bj，
a
1
,
a
2
,
.
.
.
,
a
i
a_1,a_2,…,a_{i}
a1,a2,…,ai 就可以变成
b
1
,
b
2
,
.
.
.
b
j
b_1,b_2,…b_{j}
b1,b2,…bj。替换时需要考虑
a
i
=
b
j
a_i=b_j
ai=bj 和
a
i
≠
b
j
a_i \neq b_j
ai=bj 的情况，所以替换产生的消耗为：
f
[
i
−
1
]
[
j
−
1
]
{
0
a
i
=
b
j
R
a
i
≠
b
j
f[i-1][j-1] + \begin{cases} 0 & a_i=b_j \ R & a_i \neq b_j\end{cases}
f[i−1][j−1]+{0Rai=bjai=bj 如图所示，源字符串为 “AGTA”，目标字符串为 “GATCGT” 的情况下，将 “AGT” 变成 “GATCGT” 的最小消耗为
f
[
i
−
1
]
[
j
−
1
]
f[i-1][j-1]
f[i−1][j−1]，那么只要将 源字符串 的最后一个字符 替换为 目标字符串 的最后一个字符 ，就可以把源字符串变成目标字符串；替换时根据 源字符串 和 目标字符串 原本是否相等来决定消耗；
- 边界情况主要考虑以下几种：
a. 空串变成目标串 即
f
[
0
]
[
j
]
f[0][j]
f[0][j]，总共需要插入
j
j
j 个字符，所以
f
[
0
]
[
j
]
=
f
[
0
]
[
j
−
1
]
I
f[0][j] = f[0][j-1] + I
f[0][j]=f[0][j−1]+I；
b. 源字符串变成空串 即
f
[
i
]
[
0
]
f[i][0]
f[i][0]，总共需要删除
i
i
i 个字符，所以
f
[
i
]
[
0
]
=
f
[
i
−
1
]
[
0
]
D
f[i][0] = f[i-1][0] + D
f[i][0]=f[i−1][0]+D；
c. 空串变成空串 即
f
[
0
]
[
0
]
=
0
f[0][0] = 0
f[0][0]=0
将上述所有状态进行一个整合，得到状态转移方程如下：
f
[
i
]
[
j
]
=
{
0
i
=
0
,
j
=
0
f
[
i
]
[
j
−
1
]
I
i
=
0
,
j
0
f
[
i
−
1
]
[
j
]
D
i
0
,
j
=
0
min
i
0
,
j
0
{
f
[
i
]
[
j
−
1
]
I
f
[
i
−
1
]
[
j
]
D
f
[
i
−
1
]
[
j
−
1
]
R
a
i
≠
b
j
f[i][j] = \begin{cases}0 & i=0,j=0\f[i][j-1]+I & i=0,j>0\ f[i-1][j] + D & i>0,j=0 \ \min_{i>0,j>0} \begin{cases} f[i][j-1] + I\ f[i-1][j] + D\ f[i-1][j-1] + R_{a_i \neq b_j}\end{cases}\end{cases}
f[i][j]=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧0f[i][j−1]+If[i−1][j]+Dmini>0,j>0⎩⎪⎨⎪⎧f[i][j−1]+If[i−1][j]+Df[i−1][j−1]+Rai=bji=0,j=0i=0,j>0i>0,j=0
通过这个状态矩阵，最后计算得到
f
[
n
]
[
m
]
f[n][m]
f[n][m] 就是该题所求 "源字符串
a
1
,
a
2
,
.
.
.
,
a
n
a_1,a_2,…,a_n
a1,a2,…,an，经过 插入、删除、替换 变成目标字符串
b
1
,
b
2
,
.
.
.
b
m
b_1,b_2,…b_m
b1,b2,…bm" 的最少消耗了，特殊的，当
I
=
D
=
R
=
1
I = D = R = 1
I=D=R=1 时，
f
[
n
]
[
m
]
f[n][m]
f[n][m] 就是字符串
a
a
a 和
b
b
b 的莱文斯坦距离。
状态总数
O
(
n
m
)
O(nm)
O(nm)，每次状态转移的消耗为
O
(
1
)
O(1)
O(1)，所以总的时间复杂度为
O
(
n
m
)
O(nm)
O(nm)，空间上可以采用滚动数组进行优化，具体优化方案可以参考 最长公共子序列 的求解过程。
如图所示的是一张源字符串 “AGTACG” 到目标字符串 “GATCGTGAGC” 的莱文斯坦距离图。
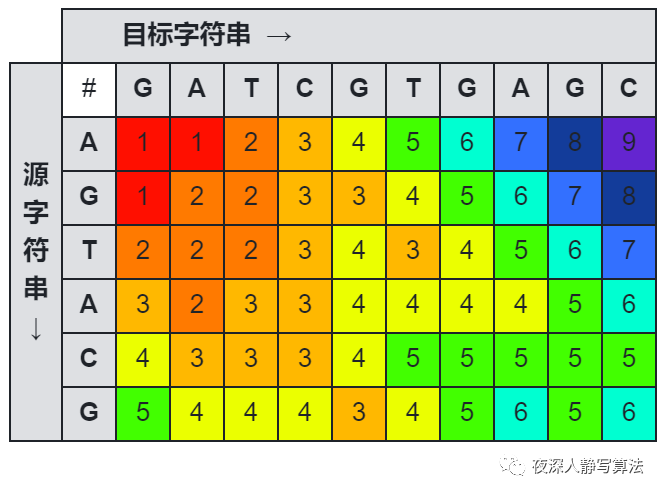
有关最小编辑距离的详细内容，可以参考：夜深人静写算法（二十二）- 最小编辑距离。
3、双串匹配问题
给定一个 匹配字符串 s (只包含小写字母) 和一个 模式字符串 p (包含小写字母和两种额外字符：
'.'和'*')，要求实现一个支持'.'和'*'的正则表达式匹配（'*'前面保证有字符）。
'.'匹配任意单个字符
'*'匹配零个或多个前面的那一个元素
这是个经典的 串匹配 问题，可以按照 最长公共子序列 的思路去解决。令
f
(
i
,
j
)
f(i, j)
f(i,j) 代表的是 匹配串前缀 s[0:i] 和 模式串前缀 p[0:j] 是否有匹配，只有两个值： 0 代表 不匹配， 1 代表 匹配。
于是，对模式串进行分情况讨论：
1）当 p[j] 为.时，代表 s[i] 为任意字符时，它都能够匹配（没毛病吧？没毛病），所以问题就转化成了求 匹配串前缀 s[0:i-1] 和 模式串前缀 p[0:j-1] 是否有匹配的问题，也就是这种情况下
f
(
i
,
j
)
=
f
(
i
−
1
,
j
−
1
)
f(i, j) = f(i-1, j-1)
f(i,j)=f(i−1,j−1)，如图1所示：
2）当 p[j] 为*时，由于*前面保证有字符，所以拿到字符 p[j-1]，分情况讨论：
2.a）如果 p[j-1] 为.时，可以匹配所有 s[0:i] 的后缀，这种情况下，只要
f
(
k
,
j
−
2
)
f(k, j-2)
f(k,j−2) 为 1，
f
(
i
,
j
)
f(i, j)
f(i,j) 就为 1；其中
k
∈
[
0
,
i
]
k \in [0, i]
k∈[0,i]。如下图所示：
2.b）如果 p[j-1] 非.时，只有当 s[0:i] 的后缀 字符全为 p[j-1] 时，才能去匹配 s[0:i] 的前缀，同样转化成
f
(
k
,
j
−
2
)
f(k, j-2)
f(k,j−2) 的子问题。如下图所示：
3）当 p[j] 为其他任意字符时，一旦 p[j] 和 s[i] 不匹配，就认为
f
(
i
,
j
)
=
0
f(i, j) = 0
f(i,j)=0，否则
f
(
i
,
j
)
=
f
(
i
−
1
,
j
−
1
)
f(i, j) = f(i-1, j-1)
f(i,j)=f(i−1,j−1)，如下图所示：
最后，这个问题可以采用 记忆化搜索 求解，并且需要考虑一些边界条件，边界条件可以参考代码实现中的讲解。记忆化搜索会在下文仔细讲解。
匹配串的长度为
n
n
n，模式串的长度为
m
m
m。状态数：
O
(
n
m
)
O(nm)
O(nm)，状态转移：
O
(
n
)
O(n)
O(n)，时间复杂度：
O
(
n
2
m
)
O(n^2m)
O(n2m)。
四、记忆化搜索
给定一个
n
(
n
≤
45
)
n(n \le 45)
n(n≤45)，求 斐波那契数列的第
n
n
n 项的值，要求用递归实现。
那么，我们只需要套用上面的递归函数，并且处理好递归出口，就能把它写成递归的形式，C语言 代码实现如下：
int f(unsigned int n) {
if(n <= 1) {
return 1;
}
return f(n-1) + f(n-2);
}
递归求解的过程如下：
这是一棵二叉树，树的高度为
n
n
n，所以粗看递归访问时结点数为
2
n
2^n
2n，但是仔细看，对于任何一棵子树而言，左子树的高度一定比右子树的高度大，所以不是一棵严格的完全二叉树。为了探究它实际的时间复杂度，我们改下代码：
int f(unsigned int n) {
++c[n];
if(n <= 1) {
return 1;
}
return f(n-1) + f(n-2);
}
加了一句代码 ++c[n];，引入一个计数器，来看下在不同的
n
n
n 的情况下，
f
(
n
)
f(n)
f(n) 这个函数的调用次数，如图所示：
观察
c
[
n
]
c[n]
c[n] 的增长趋势，首先排除等差数列，然后再来看是否符合等比数列，我们来尝试求下
c
[
n
]
/
c
[
n
−
1
]
c[n] / c[n-1]
c[n]/c[n−1] 的值，列出表格如下：
观察发现，随着
n
n
n 的不断增大，
c
[
n
]
/
c
[
n
−
1
]
c[n]/c[n-1]
c[n]/c[n−1] 越来越接近一个常数，而这个常数就是黄金分割的倒数：
2
5
−
1
≈
1.618034
\frac {2}{ \sqrt 5 - 1} \approx 1.618034
5
−12≈1.618034 当
n
n
n 趋近于无穷大的时候，满足如下公式：
c
[
n
]
=
2
5
−
1
c
[
n
−
1
]
c[n] = \frac {2}{ \sqrt 5 - 1} c[n-1]
c[n]=5
−12c[n−1] 对等比数列化解后累乘得到：
c
[
n
]
=
2
5
−
1
c
[
n
−
1
]
=
(
2
5
−
1
)
2
c
[
n
−
2
]
=
(
2
5
−
1
)
n
\begin{aligned}c[n] &= \frac {2}{ \sqrt 5 - 1} c[n-1]\ &= (\frac {2}{ \sqrt 5 - 1})^2 c[n-2]\ &= (\frac {2}{ \sqrt 5 - 1})^n \end{aligned}
c[n]=5
−12c[n−1]=(5
−12)2c[n−2]=(5
−12)n 所以，斐波那契数列递归求解的时间复杂度就是 ：
O
(
(
2
5
−
1
)
n
)
O((\frac {2}{ \sqrt 5 - 1})^n)
O((5
−12)n)
这是一个指数级的算法，随着
n
n
n 的不断增大，时间消耗呈指数级增长，我们在写代码的时候肯定是要避免这样的写法的，尤其是在服务器开发过程中，CPU 是一种极其宝贵的资源，任何的浪费都是可耻的。但是，面试官又要求用递归实现，真是太讨厌了！
那么，怎么来优化这里的算力消耗呢？
递归求解斐波那契数列其实是一个深度优先搜索的过程，它是毫无优化的暴力枚举，对于
f
(
5
)
f(5)
f(5) 的求解，如图所示：
同时，我们也发现，计算过程中其实有很多重叠子问题，例如
f
(
3
)
f(3)
f(3) 被计算了
2
2
2 次，如图所示：
f
(
2
)
f(2)
f(2) 被计算了
3
3
3 次，如图所示：
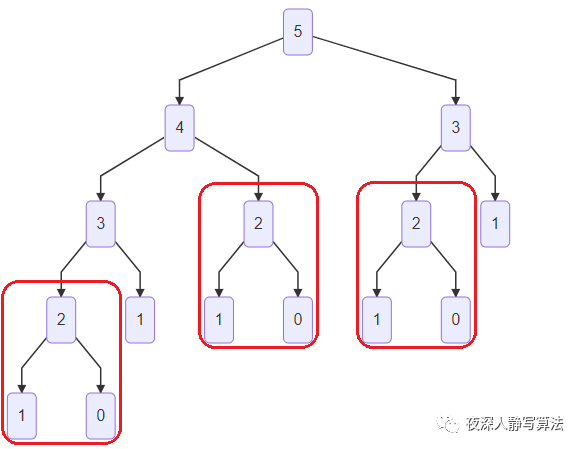
所以如果我们能够确保每个
f
(
i
)
f(i)
f(i) 只被计算一次，问题就迎刃而解了。可以考虑将
f
(
i
)
f(i)
f(i) 计算出来的值存储到哈希数组
h
[
i
]
h[i]
h[i] 中，当第二次要访问
f
(
i
)
f(i)
f(i) 时，直接取
h
[
i
]
h[i]
h[i] 的值即可，这样每次计算
f
(
i
)
f(i)
f(i) 的时间复杂度变成了
O
(
1
)
O(1)
O(1)，总共需要计算
f
(
2
)
,
f
(
3
)
,
.
.
.
f
(
n
)
f(2),f(3),…f(n)
f(2),f(3),…f(n)，总的时间复杂度就变成了
O
(
n
)
O(n)
O(n) 。
这种用哈希数组来记录运算结果，避免重复运算的方法就是记忆化搜索。
这件事情如何执行下去呢？
我们用一个数组
h
[
i
]
h[i]
h[i] 来记录 斐波那契数列 第
i
i
i 项的值，把之前的递归代码改成如下形式：
const int inf = -1;
int h[46];
void init() {
memset(h, inf, sizeof(h)); // 1）
}
int f(unsigned int n) {
if(n <= 1) {
return 1;
}
int &fib = h[n]; // 2）
if(fib != inf) {
return fib; // 3）
}
fib = f(n-1) + f(n-2); // 4）
return fib;
}
- 1）初始化所有
f
(
i
)
f(i)
f(i) 都没有被计算过，为了方便用 memset，可以将 inf定义成 -1；
- 2）注意这里用了个引用，而且一定要用引用，具体原因留给读者自己思考，当然不想思考的话，下文也会讲到，不必担心；
- 3）当
fib也就是h[n]已经计算过了，那么直接返回结果即可； - 4）最后，利用递归计算
h[n]的值，并且返回结果；
和递归版本相比，多了这么一段代码：
int &fib = h[n];
if(fib != inf) {
return fib;
}
那么它的作用体现在哪里呢？我们通过一个动图来感受一下：
如图所示，当第二次需要计算
f
(
2
)
f(2)
f(2) 和
f
(
3
)
f(3)
f(3) 时，由于结果已经计算出来并且存储在
h
[
2
]
h[2]
h[2] 和
h
[
3
]
h[3]
h[3] 中，所以上面这段代码的fib != inf表达式为真，直接返回，不再需要往下递归计算，这样就把原本的 “递归二叉树” 转换成了 “递归链”， 从而将原本指数级的算法变成了多项式级别。
上文用一个简单的例子阐述了记忆化搜索的实现方式，并且提到了利用数组来记录已经计算出来的重叠子问题，这个和动态规划的思想非常相似，没错，记忆化搜索其实用的就是动态规划的思想。更加确切的说，可以用如下公式来表示：
记忆化搜索 = 深度优先搜索的实现 + 动态规划的思想
有关记忆化搜索的更多内容，可以参考：
夜深人静写算法（二十六）- 记忆化搜索。
五、背包问题
1、0/1 背包
有
n
(
n
≤
100
)
n(n \le100)
n(n≤100) 个物品和一个容量为
m
(
m
≤
10000
)
m(m \le 10000)
m(m≤10000) 的背包。第
i
i
i 个物品的容量是
c
[
i
]
c[i]
c[i]，价值是
w
[
i
]
w[i]
w[i]。现在需要选择一些物品放入背包，并且总容量不能超过背包容量，求能够达到的物品的最大总价值。
以上就是 0/1 背包问题的完整描述，之所以叫 0/1 背包，是因为每种物品只有一个，可以选择放入背包或者不放，而 0 代表不放，1 代表放。
第一步：设计状态；
状态
(
i
,
j
)
(i, j)
(i,j) 表示前
i
i
i 个物品恰好放入容量为
j
j
j 的背包
(
i
∈
[
0
,
n
]
,
j
∈
[
0
,
m
]
)
(i \in [0, n], j \in [0, m])
(i∈[0,n],j∈[0,m])；
令
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 表示状态
(
i
,
j
)
(i, j)
(i,j) 下该背包得到的最大价值，即前
i
i
i 个物品恰好放入容量为
j
j
j 的背包所得到的最大总价值；
第二步：列出状态转移方程；
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
]
,
d
p
[
i
−
1
]
[
j
−
c
[
i
]
]
w
[
i
]
)
dp[i][j] = max(dp[i-1][j], dp[i-1][j - c[i]] + w[i])
dp[i][j]=max(dp[i−1][j],dp[i−1][j−c[i]]+w[i]) 因为每个物品要么放，要么不放，所以只需要考虑第
i
i
i 个物品 放 或 不放 的情况：
1）不放：如果 “第
i
i
i 个物品不放入容量为
j
j
j 的背包”，那么问题转化成求 “前
i
−
1
i-1
i−1 个物品放入容量为
j
j
j 的背包” 的问题；由于不放，所以最大价值就等于 “前
i
−
1
i-1
i−1 个物品放入容量为
j
j
j 的背包” 的最大价值，即
d
p
[
i
−
1
]
[
j
]
dp[i-1][j]
dp[i−1][j]；
2）放：如果 “第
i
i
i 个物品放入容量为
j
j
j 的背包”，那么问题转化成求 “前
i
−
1
i-1
i−1 个物品放入容量为
j
−
c
[
i
]
j-c[i]
j−c[i] 的背包” 的问题；那么此时最大价值就等于 “前
i
−
1
i-1
i−1 个物品放入容量为
j
−
c
[
i
]
j-c[i]
j−c[i] 的背包” 的最大价值 加上放入第
i
i
i 个物品的价值，即
d
p
[
i
−
1
]
[
j
−
c
[
i
]
]
w
[
i
]
dp[i-1][j - c[i]] + w[i]
dp[i−1][j−c[i]]+w[i]；
将以上两种情况取大者，就是我们所求的 “前
i
i
i 个物品恰好放入容量为
j
j
j 的背包” 的最大价值了。
我们发现，当状态在进行转移的时候，
(
i
,
j
)
(i, j)
(i,j) 不是来自
(
i
−
1
,
j
)
(i-1, j)
(i−1,j)，就是来自
(
i
−
1
,
j
−
c
[
i
]
)
(i-1, j - c[i])
(i−1,j−c[i])，所以必然有一个初始状态，而这个初始状态就是
(
0
,
0
)
(0, 0)
(0,0)，含义是 “前 0 个物品放入一个背包容量为 0 的背包”，这个状态下的最大价值为 0，即
d
p
[
0
]
[
0
]
=
0
dp[0][0] = 0
dp[0][0]=0；
那么我们再来考虑，
(
0
,
3
)
(0, 3)
(0,3) 是什么意思呢？它代表的是 “前 0 个物品恰好放入一个背包容量为 3 的背包”，明显这种情况是不存在的，因为 0 个物品的价值肯定是 0。所以这种状态被称为非法状态，非法状态是无法进行状态转移的，于是我们可以通过初始状态和非法状态进所有状态进行初始化。
d
p
[
0
]
[
i
]
=
{
0
i
=
0
i
n
f
i
0
dp[0][i] = \begin{cases} 0 & i = 0\ inf & i > 0\end{cases}
dp[0][i]={0infi=0i>0
其中
i
n
f
inf
inf 在程序实现时，我们可以设定一个非常小的数，比如
−
1000000000
-1000000000
−1000000000，只要保证无论如何状态转移它都不能成为最优解的候选状态。为了加深状态转移的概念，来看图二-5-1 的一个例子，每个格子代表一个状态，
(
0
,
0
)
(0,0)
(0,0) 代表初始状态，蓝色的格子代表已经求得的状态，灰色的格子代表非法状态，红色的格子代表当前正在进行转移的状态，图中的第
i
i
i 行代表了前
i
i
i 个物品对应容量的最优值，第 4 个物品的容量为 2，价值为 8，则有状态转移如下：
d
p
[
4
]
[
4
]
=
m
a
x
(
d
p
[
4
−
1
]
[
4
]
,
d
p
[
4
−
1
]
[
4
−
2
]
8
)
=
m
a
x
(
d
p
[
3
]
[
4
]
,
d
p
[
3
]
[
2
]
8
)
\begin{aligned} dp[4][4] &= max( dp[4-1][4], dp[4-1][4 - 2] + 8) \ &= max( dp[3][4], dp[3][2] + 8) \end{aligned}
dp[4][4]=max(dp[4−1][4],dp[4−1][4−2]+8)=max(dp[3][4],dp[3][2]+8)
有关 0/1 背包的更多内容，可以参考：夜深人静写算法（十四）- 0/1 背包。
2、完全背包
有
n
(
n
≤
100
)
n(n \le 100)
n(n≤100) 种物品和一个容量为
m
(
m
≤
10000
)
m(m \le 10000)
m(m≤10000) 的背包。第
i
i
i 种物品的容量是
c
[
i
]
c[i]
c[i]，价值是
w
[
i
]
w[i]
w[i]。现在需要选择一些物品放入背包，每种物品可以无限选择，并且总容量不能超过背包容量，求能够达到的物品的最大总价值。
以上就是完全背包问题的完整描述，和 0/1 背包的区别就是每种物品可以无限选取，即文中红色字体标注的内容；
第一步：设计状态；
状态
(
i
,
j
)
(i, j)
(i,j) 表示前
i
i
i 种物品恰好放入容量为
j
j
j 的背包
(
i
∈
[
0
,
n
]
,
j
∈
[
0
,
m
]
)
(i \in [0, n], j \in [0, m])
(i∈[0,n],j∈[0,m])；
令
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 表示状态
(
i
,
j
)
(i, j)
(i,j) 下该背包得到的最大价值，即前
i
i
i 种物品（每种物品可以选择无限件）恰好放入容量为
j
j
j 的背包所得到的最大总价值；
第二步：列出状态转移方程；
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
w
[
i
]
∗
k
)
dp[i][j] = max(dp[i-1][j - c[i]*k] + w[i]*k)
dp[i][j]=max(dp[i−1][j−c[i]∗k]+w[i]∗k)
(
0
≤
k
≤
j
c
[
i
]
)
(0 \le k \le \frac {j} {c[i]})
(0≤k≤c[i]j)
- 因为每种物品有无限种可放置，将它归类为以下两种情况：
1）不放：如果 “第
i
i
i 种物品不放入容量为
j
j
j 的背包”，那么问题转化成求 “前
i
−
1
i-1
i−1 种物品放入容量为
j
j
j 的背包” 的问题；由于不放，所以最大价值就等于 “前
i
−
1
i-1
i−1 种物品放入容量为
j
j
j 的背包” 的最大价值，对应状态转移方程中
k
=
0
k = 0
k=0 的情况， 即
d
p
[
i
−
1
]
[
j
]
dp[i-1][j]
dp[i−1][j]；
2）放 k 个：如果 “第
i
i
i 种物品放入容量为
j
j
j 的背包”，那么问题转化成求 “前
i
−
1
i-1
i−1 种物品放入容量为
j
−
c
[
i
]
∗
k
j-c[i]*k
j−c[i]∗k 的背包” 的问题；那么此时最大价值就等于 “前
i
−
1
i-1
i−1 种物品放入容量为
j
−
c
[
i
]
∗
k
j-c[i]*k
j−c[i]∗k 的背包” 的最大价值 加上放入
k
k
k 个第
i
i
i 种物品的价值，即
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
w
[
i
]
∗
k
dp[i-1][j - c[i]*k] + w[i]*k
dp[i−1][j−c[i]∗k]+w[i]∗k；
枚举所有满足条件的
k
k
k 就是我们所求的 “前
i
i
i 种物品恰好放入容量为
j
j
j 的背包” 的最大价值了。注意：由于每件物品都可以无限选择，所以这里描述的时候都是用的 “种” 作为单位，即代表不同种类的物品。
对于
n
n
n 种物品放入一个容量为
m
m
m 的背包，状态数为
O
(
n
m
)
O(nm)
O(nm)，每次状态转移的消耗为
O
(
k
)
O(k)
O(k)，所以整个状态转移的过程时间复杂度是大于
O
(
n
m
)
O(nm)
O(nm) 的，那么实际是多少呢？考虑最坏情况下，即
c
[
i
]
=
1
c[i] = 1
c[i]=1 时，那么要计算的
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 的转移数为
j
j
j，总的状态转移次数就是
m
(
m
1
)
2
\frac {m(m + 1)} {2}
2m(m+1)，所以整个算法的时间复杂度是
O
(
n
m
2
)
O(nm^2)
O(nm2) 的，也就是说状态转移均摊时间复杂度是
O
(
m
)
O(m)
O(m) 的。
我们把状态转移方程进行展开后得到如下的
k
1
k+1
k+1 个式子：
d
p
[
i
]
[
j
]
=
m
a
x
{
d
p
[
i
−
1
]
[
j
]
(
1
)
d
p
[
i
−
1
]
[
j
−
c
[
i
]
]
w
[
i
]
(
2
)
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
2
]
w
[
i
]
∗
2
(
3
)
.
.
.
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
w
[
i
]
∗
k
(
k
1
)
dp[i][j] = max \begin{cases} dp[i-1][j] & (1)\ dp[i-1][j - c[i]] + w[i] & (2)\ dp[i-1][j - c[i]*2] + w[i]*2 & (3)\ … \ dp[i-1][j - c[i]*k] + w[i] *k & (k+1) \end{cases}
dp[i][j]=max⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧dp[i−1][j]dp[i−1][j−c[i]]+w[i]dp[i−1][j−c[i]∗2]+w[i]∗2…dp[i−1][j−c[i]∗k]+w[i]∗k(1)(2)(3)(k+1)
利用待定系数法，用
j
−
c
[
i
]
j-c[i]
j−c[i] 代替上式的
j
j
j 得到如下式子：
d
p
[
i
]
[
j
−
c
[
i
]
]
=
m
a
x
{
d
p
[
i
−
1
]
[
j
−
c
[
i
]
]
(
1
)
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
2
]
w
[
i
]
(
2
)
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
3
]
w
[
i
]
∗
2
(
3
)
.
.
.
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
w
[
i
]
∗
(
k
−
1
)
(
k
)
dp[i][j-c[i]] = max \begin{cases} dp[i-1][j-c[i]] & (1)\ dp[i-1][j - c[i]*2] + w[i] & (2)\ dp[i-1][j - c[i]*3] + w[i]*2 & (3)\ … \ dp[i-1][j - c[i]*k] + w[i] *(k-1) & (k) \end{cases}
dp[i][j−c[i]]=max⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧dp[i−1][j−c[i]]dp[i−1][j−c[i]∗2]+w[i]dp[i−1][j−c[i]∗3]+w[i]∗2…dp[i−1][j−c[i]∗k]+w[i]∗(k−1)(1)(2)(3)(k)
等式两边都加上
w
[
i
]
w[i]
w[i] 得到：
d
p
[
i
]
[
j
−
c
[
i
]
]
w
[
i
]
=
m
a
x
{
d
p
[
i
−
1
]
[
j
−
c
[
i
]
]
w
[
i
]
(
1
)
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
2
]
w
[
i
]
∗
2
(
2
)
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
3
]
w
[
i
]
∗
3
(
3
)
.
.
.
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
w
[
i
]
∗
k
(
k
)
dp[i][j-c[i]] + w[i] = max \begin{cases} dp[i-1][j-c[i]] + w[i] & (1)\ dp[i-1][j - c[i]*2] + w[i]*2 & (2)\ dp[i-1][j - c[i]*3] + w[i]*3 & (3)\ … \ dp[i-1][j - c[i]*k] + w[i] *k & (k) \end{cases}
dp[i][j−c[i]]+w[i]=max⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧dp[i−1][j−c[i]]+w[i]dp[i−1][j−c[i]∗2]+w[i]∗2dp[i−1][j−c[i]∗3]+w[i]∗3…dp[i−1][j−c[i]∗k]+w[i]∗k(1)(2)(3)(k)
于是我们发现，这里的
(
1
)
.
.
.
(
k
)
(1)…(k)
(1)…(k) 式子等价于最开始的状态转移方程中的
(
2
)
.
.
.
(
k
1
)
(2) … (k+1)
(2)…(k+1) 式，所以原状态转移方程可以简化为：
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
]
,
d
p
[
i
]
[
j
−
c
[
i
]
]
w
[
i
]
)
dp[i][j] = max(dp[i-1][j], dp[i][j-c[i]] + w[i])
dp[i][j]=max(dp[i−1][j],dp[i][j−c[i]]+w[i])
这样就把原本均摊时间复杂度为
O
(
m
)
O(m)
O(m) 的状态转移优化到了
O
(
1
)
O(1)
O(1)。
那么我们来理解一下这个状态转移方程的含义：对于第
i
i
i 种物品，其实只有两种选择：一个都不放、至少放一个；一个都不放 就是 “前
i
−
1
i-1
i−1 种物品放满一个容量为
j
j
j 的背包” 的情况，即
d
p
[
i
−
1
]
[
j
]
dp[i-1][j]
dp[i−1][j]；至少放一个 的话，我们尝试在 “前
i
i
i 种物品放满一个容量为
j
j
j 的背包” 里拿掉 1 个物品，即 “前
i
i
i 种物品放满一个容量为
j
−
c
[
i
]
j-c[i]
j−c[i] 的背包”，这时候的值就是
d
p
[
i
]
[
j
−
c
[
i
]
]
w
[
i
]
dp[i][j-c[i]] + w[i]
dp[i][j−c[i]]+w[i]。取两者的大者就是答案了。
其实这个思路我可以在本文开头就讲，也容易理解，之所以引入优化以及逐步推导的过程，就是想告诉读者，很多动态规划的问题是不能套用模板的，从简单的思路出发，加上一些推导和优化，逐步把复杂的问题循序渐进的求出来，才是解决问题的普遍思路。
有关完全背包的更多内容，可以参考：夜深人静写算法（十五）- 完全背包。
3、多重背包
有
n
(
n
≤
100
)
n(n \le 100)
n(n≤100) 种物品和一个容量为
m
(
m
≤
10000
)
m(m \le 10000)
m(m≤10000) 的背包。第
i
i
i 种物品的容量是
c
[
i
]
c[i]
c[i]，价值是
w
[
i
]
w[i]
w[i]。现在需要选择一些物品放入背包，每种物品可以选择
x
[
i
]
x[i]
x[i] 件，并且总容量不能超过背包容量，求能够达到的物品的最大总价值。
以上就是多重背包问题的完整描述，和 0/1 背包、完全背包的区别就是每种物品的选取有物品自己的值域限制，即文中红色字体标注的内容；
第一步：设计状态；
状态
(
i
,
j
)
(i, j)
(i,j) 表示前
i
i
i 种物品恰好放入容量为
j
j
j 的背包
(
i
∈
[
0
,
n
]
,
j
∈
[
0
,
m
]
)
(i \in [0, n], j \in [0, m])
(i∈[0,n],j∈[0,m])；
令
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 表示状态
(
i
,
j
)
(i, j)
(i,j) 下该背包得到的最大价值，即前
i
i
i 种物品（每种物品可以选择
x
[
i
]
x[i]
x[i] 件）恰好放入容量为
j
j
j 的背包所得到的最大总价值；
第二步：列出状态转移方程；
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
w
[
i
]
∗
k
)
(
0
≤
k
≤
x
[
i
]
)
dp[i][j] = max(dp[i-1][j - c[i]*k] + w[i]*k) \ (0 \le k \le x[i])
dp[i][j]=max(dp[i−1][j−c[i]∗k]+w[i]∗k)(0≤k≤x[i]) 因为每种物品有
x
[
i
]
x[i]
x[i] 种可放置，将它归类为以下两种情况：
1）不放：如果 “第
i
i
i 种物品不放入容量为
j
j
j 的背包”，那么问题转化成求 “前
i
−
1
i-1
i−1 种物品放入容量为
j
j
j 的背包” 的问题；由于不放，所以最大价值就等于 “前
i
−
1
i-1
i−1 种物品放入容量为
j
j
j 的背包” 的最大价值，对应状态转移方程中
k
=
0
k = 0
k=0 的情况， 即
d
p
[
i
−
1
]
[
j
]
dp[i-1][j]
dp[i−1][j]；
2）放 k 个：如果 “第
i
i
i 种物品放入容量为
j
j
j 的背包”，那么问题转化成求 “前
i
−
1
i-1
i−1 种物品放入容量为
j
−
c
[
i
]
∗
k
j-c[i]*k
j−c[i]∗k 的背包” 的问题；那么此时最大价值就等于 “前
i
−
1
i-1
i−1 种物品放入容量为
j
−
c
[
i
]
∗
k
j-c[i]*k
j−c[i]∗k 的背包” 的最大价值 加上放入
k
k
k 个第
i
i
i 种物品的价值，即
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
w
[
i
]
∗
k
dp[i-1][j - c[i]*k] + w[i]*k
dp[i−1][j−c[i]∗k]+w[i]∗k；
枚举所有满足条件的
k
k
k 就是我们所求的 “前
i
i
i 种物品恰好放入容量为
j
j
j 的背包” 的最大价值了。
多重背包问题是背包问题的一般情况，每种物品有自己的值域限制。如果从状态转移方程出发，我们可以把三种背包问题进行归纳统一，得到一个统一的状态转移方程如下：
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
w
[
i
]
∗
k
)
dp[i][j] = max(dp[i-1][j - c[i]*k] + w[i]*k)
dp[i][j]=max(dp[i−1][j−c[i]∗k]+w[i]∗k) 对于 0/1 背包问题，
k
k
k 的取值为
0
,
1
0,1
0,1；
对于完全背包问题，
k
k
k 的取值为
0
,
1
,
2
,
3
,
.
.
.
,
⌊
j
c
[
i
]
⌋
0, 1, 2, 3, …, \lfloor \frac j {c[i]} \rfloor
0,1,2,3,…,⌊c[i]j⌋；
对于多重背包问题，
k
k
k 的取值为
0
,
1
,
2
,
3
,
.
.
.
,
x
[
i
]
0, 1, 2, 3, …, x[i]
0,1,2,3,…,x[i]；
对于
n
n
n 种物品放入一个容量为
m
m
m 的背包，状态数为
O
(
n
m
)
O(nm)
O(nm)，每次状态转移的消耗为
O
(
x
[
i
]
)
O(x[i])
O(x[i])，所以整个状态转移的过程时间复杂度是大于
O
(
n
m
)
O(nm)
O(nm) 的，那么实际是多少呢？
考虑最坏情况下，即
x
[
i
]
=
m
x[i] = m
x[i]=m 时，那么要计算的
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 的转移数为
j
j
j，总的状态转移次数就是
m
(
m
1
)
2
\frac {m(m + 1)} {2}
2m(m+1)，所以整个算法的时间复杂度是
O
(
n
m
2
)
O(nm^2)
O(nm2) 的，也就是说状态转移均摊时间复杂度是
O
(
m
)
O(m)
O(m) 的。
一个容易想到的优化是：我们可以将每种物品拆成
x
[
i
]
x[i]
x[i] 个，这样变成了
∑
i
=
1
n
x
[
i
]
\sum_{i=1}^n x[i]
∑i=1nx[i] 个物品的 0/1 背包问题，我们知道 0/1 背包问题优化完以后，空间复杂度只和容量有关，即
O
(
m
)
O(m)
O(m)。
所以多重背包问题的空间复杂度至少是可以优化到
O
(
m
)
O(m)
O(m) 的。
然而， 如果这样拆分，时间复杂度还是没有变化，但是给我们提供了一个思路，就是每种物品是可以拆分的。假设有
x
[
i
]
x[i]
x[i] 个物品，我们可以按照 2 的幂进行拆分，把它拆分成：
1
,
2
,
4
,
.
.
.
,
2
k
−
1
,
x
[
i
]
−
2
k
1
1, 2, 4, …, 2^{k-1}, x[i] - 2^{k} + 1
1,2,4,…,2k−1,x[i]−2k+1
其中
k
k
k 是最大的满足
x
[
i
]
−
2
k
1
≥
0
x[i] - 2^{k} + 1 \ge 0
x[i]−2k+1≥0 的非负整数。
这样，1 到
x
[
i
]
x[i]
x[i] 之间的所有整数都能通过以上
k
1
k+1
k+1 个数字组合出来，所以只要拆成以上
k
1
k+1
k+1 个物品，所有取
k
(
0
≤
k
≤
x
[
i
]
)
k (0 \le k \le x[i])
k(0≤k≤x[i]) 个物品的情况都能被考虑进来。
举例说明，当
x
[
i
]
=
14
x[i] = 14
x[i]=14 时，可以拆分成 1,2,4,7 个物品，那么当我们要取 13 个这类物品的时候，相当于选择 2、4、7，容量分别为
c
[
i
]
∗
2
,
c
[
i
]
∗
4
,
c
[
i
]
∗
7
c[i]*2, c[i]*4, c[i]* 7
c[i]∗2,c[i]∗4,c[i]∗7, 价值分别为
w
[
i
]
∗
2
,
w
[
i
]
∗
4
,
w
[
i
]
∗
7
w[i]*2, w[i]*4, w[i]* 7
w[i]∗2,w[i]∗4,w[i]∗7。
通过这种拆分方式，
x
[
i
]
x[i]
x[i] 最多被拆分成
l
o
g
2
x
[
i
]
log_2 {x[i]}
log2x[i] 个物品，然后再用 0/1 背包求解，得到了一个时间复杂度为
O
(
m
∑
i
=
1
n
l
o
g
2
x
[
i
]
)
O(m\sum_{i=1}^{n}log_2{x[i]})
O(m∑i=1nlog2x[i]) 的算法。
有关多重背包的更多内容，可以参考：夜深人静写算法（十六）- 多重背包。
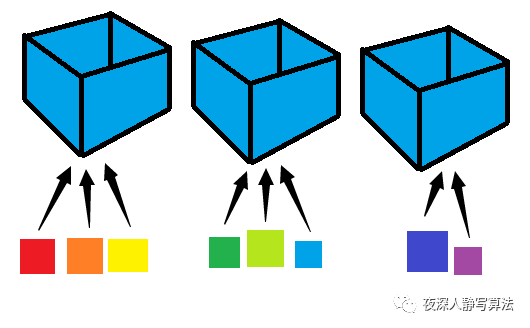
4、分组背包
有
n
(
n
≤
1000
)
n(n \le 1000)
n(n≤1000) 个物品和一个容量为
m
(
m
≤
1000
)
m(m \le 1000)
m(m≤1000) 的背包。这些物品被分成若干组，第
i
i
i 个物品属于
g
[
i
]
g[i]
g[i] 组，容量是
c
[
i
]
c[i]
c[i]，价值是
w
[
i
]
w[i]
w[i]，现在需要选择一些物品放入背包，并且每组最多放一个物品，总容量不能超过背包容量，求能够达到的物品的最大总价值。
以上就是分组背包问题的完整描述，和其它背包问题的区别就是每个物品多了一个组号，并且相同组内，最多只能选择一个物品放入背包；因为只有一个物品，所以读者可以暂时忘掉 完全背包 和 多重背包 的概念，在往下看之前，先回忆一下 0/1 背包的状态转移方程。
第一步：预处理；
首先把每个物品按照组号
g
[
i
]
g[i]
g[i] 从小到大排序，假设总共有
t
t
t 组，则将
g
[
i
]
g[i]
g[i] 按顺序离散到
[
1
,
t
]
[1,t]
[1,t] 的正整数。这样做的目的是为了将
g
[
i
]
g[i]
g[i] 作为下标映射到状态数组中；
第二步：设计状态；
状态
(
k
,
j
)
(k, j)
(k,j) 表示前
k
k
k 组物品恰好放入容量为
j
j
j 的背包
(
k
∈
[
0
,
t
]
,
j
∈
[
0
,
m
]
)
(k \in [0, t], j \in [0, m])
(k∈[0,t],j∈[0,m])；令
d
p
[
k
]
[
j
]
dp[k][j]
dp[k][j] 表示状态
(
k
,
j
)
(k, j)
(k,j) 下该背包得到的最大价值，即前
k
k
k 组物品（每组物品至多选一件）恰好放入容量为
j
j
j 的背包所得到的最大总价值；
第三步：列出状态转移方程：
d
p
[
k
]
[
j
]
=
m
a
x
(
d
p
[
k
−
1
]
[
j
]
,
d
p
[
k
−
1
]
[
j
−
c
[
i
]
]
w
[
i
]
)
dp[k][j] = max(dp[k-1][j], dp[k-1][j - c[i]] + w[i])
dp[k][j]=max(dp[k−1][j],dp[k−1][j−c[i]]+w[i])
k
=
g
[
i
]
k = g[i]
k=g[i]因为每个物品有只有两种情况：
1）不放：如果 “第
i
i
i 个物品（属于第
k
k
k 组）不放入容量为
j
j
j 的背包”，那么问题转化成求 “前
k
−
1
k-1
k−1 组物品放入容量为
j
j
j 的背包” 的问题；由于不放，所以最大价值就等于 “前
k
−
1
k-1
k−1 组物品放入容量为
j
j
j 的背包” 的最大价值，对应状态转移方程中的
d
p
[
k
−
1
]
[
j
]
dp[k-1][j]
dp[k−1][j]；
2）放：如果 “第
i
i
i 个物品（属于第
k
k
k 组）放入容量为
j
j
j 的背包”，那么问题转化成求 “前
k
−
1
k-1
k−1 组物品放入容量为
j
−
c
[
i
]
j-c[i]
j−c[i] 的背包” 的问题；那么此时最大价值就等于 “前
k
−
1
k-1
k−1 组物品放入容量为
j
−
c
[
i
]
j-c[i]
j−c[i] 的背包” 的最大价值 加上放入第
i
i
i 个物品的价值，即
d
p
[
k
−
1
]
[
j
−
c
[
i
]
]
w
[
i
]
dp[k-1][j - c[i]] + w[i]
dp[k−1][j−c[i]]+w[i]；
因为 前
k
−
1
k-1
k−1 组物品中一定不存在第
k
k
k 组中的物品，所以能够满足 “最多放一个” 这个条件；
对于
n
n
n 个物品放入一个容量为
m
m
m 的背包，状态数为
O
(
n
m
)
O(nm)
O(nm)，每次状态转移的消耗为
O
(
1
)
O(1)
O(1)，所以整个状态转移的过程时间复杂度是
O
(
n
m
)
O(nm)
O(nm)；
注意在分组背包求解的时候，要保证相同组的在一起求，而一开始的预处理和离散化正式为了保证这一点，这样，每个物品的组号为
g
[
i
]
=
1
,
2
,
3
,
4…
,
t
g[i] = 1,2,3,4…,t
g[i]=1,2,3,4…,t，并且我们可以把状态转移方程进一步表示成和
k
k
k 无关的，如下：
d
p
[
g
[
i
]
]
[
j
]
=
m
a
x
(
d
p
[
g
[
i
]
−
1
]
[
j
]
,
d
p
[
g
[
i
]
−
1
]
[
j
−
c
[
i
]
]
w
[
i
]
)
dp[ g[i] ][j] = max(dp[ g[i]-1][j], dp[ g[i]-1][j - c[i]] + w[i])
dp[g[i]][j]=max(dp[g[i]−1][j],dp[g[i]−1][j−c[i]]+w[i])
有关分组背包更加详细的内容，可以参考：夜深人静写算法（十七）- 分组背包。
5、依赖背包
商店里有
n
(
n
≤
50
)
n(n \le 50)
n(n≤50) 个盒子，每个盒子价钱为
p
[
i
]
(
p
[
i
]
≤
1000
)
p[i](p[i] \le 1000)
pi，价值为 0，盒子里面有一些小礼物，数量为
m
[
i
]
(
1
≤
m
[
i
]
≤
10
)
m[i](1 \le m[i] \le 10)
mi，每个小礼物描述成一个二元组
(
c
,
v
)
(c, v)
(c,v)，
c
c
c 为价钱，
v
v
v 为价值，如果要买小礼物，必须先买盒子。现在给出价钱
m
(
m
≤
100000
)
m(m \le 100000)
m(m≤100000)，求能够买到的最大价值。
这是一个比较特殊的依赖性背包问题，也是依赖背包中最简单的情况，其中盒子作为 主件，小礼物作为 附件。想要购买附件，必须先购买主件，此所谓 “依赖” ；
第一步：设计状态；
状态
(
i
,
j
)
(i, j)
(i,j) 表示前
i
i
i 个盒子购买的价钱恰好为
j
j
j
(
i
∈
[
0
,
n
]
,
j
∈
[
0
,
m
]
)
(i \in [0, n], j \in [0, m])
(i∈[0,n],j∈[0,m])；
令
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 表示状态
(
i
,
j
)
(i, j)
(i,j) 下得到的最大价值，即前
i
i
i 个盒子购买价钱为
j
j
j 的情况下所得到的最大总价值；
我们在设计状态的时候，没有把小礼物设计到状态里，那么如何进行状态转移呢？
可以这么考虑，抛开小礼物不说，每个盒子其实只有两种状态，选 和 不选；
1）选：就是要对这个盒子里的小礼物进行一次 0/1 背包；
2）不选：就和这盒子里的小礼物无关了，直接等于前
i
−
1
i-1
i−1 个盒子的最大价值，即
d
p
[
i
−
1
]
[
j
]
dp[i-1][j]
dp[i−1][j]。
那么，只要从前往后枚举所有盒子，
p
[
i
]
p[i]
p[i] 为第
i
i
i 个盒子的价钱，
w
[
i
]
w[i]
w[i] 为价值，由于这个问题下盒子是没有价值的，即
w
[
i
]
w[i]
w[i] 恒等于零；
进行如下三步操作：
1）首先，买第i
i
i 个盒子，并且不放物品；
2）然后，既然盒子都已经买下来了，就可以放心对第i
i
i 个盒子里的小礼物进行 0/1 背包了；
3）最后，对 买盒子i
i
i 和 不买盒子
i
i
i 取一次最大价值；
买第
i
i
i 个盒子，不放物品的情况肯定是从前
i
−
1
i-1
i−1 个盒子的状态推算过来的，给出状态转移方程如下：
d
p
[
i
]
[
j
]
=
{
i
n
f
j
<
p
[
i
]
(
1
)
d
p
[
i
−
1
]
[
j
−
p
[
i
]
]
w
[
i
]
j
≥
p
[
i
]
(
2
)
dp[i][j] =\begin{cases}inf & j < p[i] & (1)\dp[i-1][j - p[i]]+w[i] & j \ge p[i] & (2)\end{cases}
dp[i][j]={infdp[i−1][j−p[i]]+w[i]j<p[i]j≥p[i](1)(2)
- (1) 代表钱不够，无限凄凉；(2) 代表从 前
i
−
1
i-1
i−1 个盒子价格为
j
−
p
[
i
]
j - p[i]
j−p[i] 时，再花
p
[
i
]
p[i]
p[i] 买下第
i
i
i 个盒子的情况。这时候
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 代表的是 第
i
i
i 个盒子买下后，还没买小礼物时，容量为
j
j
j 的最大总价值；
既然盒子都已经买下来了，就可以放心对第
i
i
i 个盒子里的小礼物在
d
p
[
i
]
[
0…
m
]
dp[i][0…m]
dp[i][0…m] 上进行 0/1 背包了；所有小礼物都枚举完毕以后，得到的
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 代表的是 第
i
i
i 个盒子买下，并且买了若干小礼物后，容量为
j
j
j 的最大总价值；
最后，对买 这个盒子 和 不买这个盒子 做一次选择，即取一次最大价值，如下：
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
]
[
j
]
,
d
p
[
i
−
1
]
[
j
]
)
dp[i][j] = max(dp[i][j], dp[i-1][j])
dp[i][j]=max(dp[i][j],dp[i−1][j])
这里的
d
p
[
i
−
1
]
[
j
]
dp[i-1][j]
dp[i−1][j] 正代表的是第
i
i
i 个盒子不买的情况。
有关依赖背包的更多内容，可以参考：夜深人静写算法（十八）- 依赖背包。
六、树形DP
给定一棵
n
(
n
<
=
150
)
n(n <= 150)
n(n<=150) 个结点的树，去掉一些边，使得正好出现一个
P
P
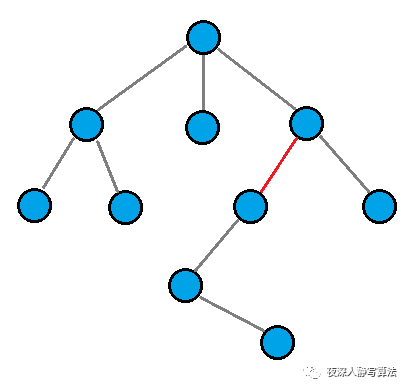
P 个结点的连通块。问去掉最少多少条边能够达到这个要求。
如图所示，一棵 10 个结点的树，我们可以去掉图中红色的边，变成两棵子树，分别为 3 个结点和 7个结点。
也可以通过这样的方式，得到三颗子树，分别为 5 、4、1 个结点。
对于树上的某个结点（如图的红色结点），可以选择去掉连接子树的边，也可以选择留着；每条连接子树的边的 选 和 不选，能够得到一个组合，对应了背包问题，而每棵子树的选择只能选择一种，对应了分组背包，所以可以利用这个思路来设计状态。
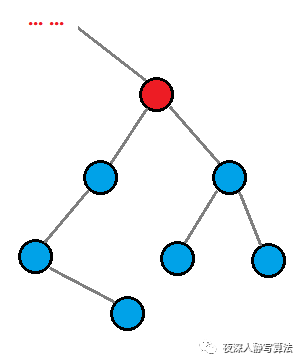
状态设计：用
d
p
[
u
]
[
x
]
dp[u][x]
dp[u][x] 表示以
u
u
u 为根的子树，能够通过去掉一些边而得到一个正好是
x
x
x 结点的连通块（注意只包含它的子树的部分，不连接它的父结点）的最少消耗；
状态转移思路：枚举
u
u
u 的所有子结点，对于子结点
v
v
v，递归计算
d
p
[
v
]
[
i
]
(
1
<
=
i
<
=
x
)
dp[v][i] (1 <= i <= x)
dp[v]i 所有的可能情况，如果
d
p
[
v
]
[
i
]
dp[v][i]
dp[v][i] 存在，则认为这是一个容量为
i
i
i，价值为
d
p
[
v
]
[
i
]
dp[v][i]
dp[v][i] 的物品，表示为
(
i
,
d
p
[
v
]
[
i
]
)
(i, dp[v][i])
(i,dp[v][i])。然后在结点
u
u
u 的背包上进行一次分组背包。
初始情况：对于任何一个结点
u
u
u，它的子结点个数为
c
u
c_u
cu，初始情况是
d
p
[
u
]
[
1
]
=
c
u
dp[u][1] = c_u
dp[u][1]=cu，表示如果以当前这个结点为孤立点，那么它的子树都不能选，所以费用就是去掉所有连接子树的边，即子树的个数。
状态转移：然后对于每棵子树
v
v
v 的
k
k
k 个结点的连通块，答案就是
d
p
[
v
]
[
j
−
k
]
d
p
[
v
]
[
k
]
−
1
dp[v][j-k] + dp[v][k] - 1
dp[v][j−k]+dp[v][k]−1，注意这里的 -1 的含义，因为我们一开始默认将所有连接子树的边去掉，所以这里需要补回来。
答案处理：最后的答案就是
min
(
d
p
[
x
]
[
P
]
(
1
i
f
x
i
s
n
o
t
r
o
o
t
)
\min(dp[x][P] + (1 \ if \ x \ is \ not \ root)
min(dp[x][P]+(1 if x is not root)；考虑结点为 P 的连通块只会出现在两个地方：1）和根结点相连的块，那么答案就是
d
p
[
r
o
o
t
]
[
P
]
dp[root][P]
dp[root][P]；2）不和根结点相连的块，需要枚举所有结点的
d
p
[
x
]
[
P
]
1
dp[x][P] +1
dp[x][P]+1 取最小值，其中这里的 1 代表斩断
(
p
a
r
e
n
t
[
x
]
,
x
)
(parent[x], x)
(parent[x],x) 这条边的消耗；
七、矩阵二分
A
n
=
[
a
11
a
12
⋯
a
1
m
a
21
a
22
⋯
a
2
m
⋮
⋮
⋱
⋮
a
m
1
a
m
2
⋯
a
m
m
]
n
A^n=\begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1m}}\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2m}}\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\ {a_{m1}}&{a_{m2}}&{\cdots}&{a_{mm}}\ \end{bmatrix}^n
An=⎣⎢⎢⎢⎡a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1ma2m⋮amm⎦⎥⎥⎥⎤n
对于求矩阵的
n
n
n 次幂，如果采用简单的连乘来求解，这个时间复杂度是完全无法接受的，我们联想到之前提到的整数的二分快速幂（夜深人静写算法（三十）- 二分快速幂），对于矩阵也是同样适用的；
A
n
=
{
I
n
=
0
(
A
n
−
1
2
)
2
×
A
n
为
奇
数
(
A
n
2
)
2
n
为
非
零
偶
数
A^{n} = \begin{cases} I & n = 0\ (A{\frac{n-1}{2}})2 \times A& n 为奇数\ (A{\frac{n}{2}})2 & n 为非零偶数 \end{cases}
An=⎩⎪⎨⎪⎧I(A2n−1)2×A(A2n)2n=0n为奇数n为非零偶数
再加上模加、模乘的性质，矩阵同样满足模幂运算，即：
A
n
m
o
d
M
=
{
I
m
o
d
M
n
=
0
(
A
n
−
1
2
)
2
×
A
m
o
d
M
n
为
奇
数
(
A
n
2
)
2
m
o
d
M
n
为
非
零
偶
数
A^{n} \mod M = \begin{cases} I \mod M & n = 0\ (A{\frac{n-1}{2}})2 \times A \mod M & n 为奇数\ (A{\frac{n}{2}})2 \mod M & n 为非零偶数 \end{cases}
AnmodM=⎩⎪⎨⎪⎧ImodM(A2n−1)2×AmodM(A2n)2modMn=0n为奇数n为非零偶数
如此一来，对于
m
m
m 阶方阵
A
A
A，时间复杂度就可以降到
O
(
m
3
l
o
g
n
)
O(m^3log_n)
O(m3logn)；
还是回到本文开头的那个问题，如何计算斐波那契数列第
n
n
n 项模上
M
M
M ？相信聪明的读者已经想到了，我们的主角是：矩阵 ！
我们首先来看递推公式：
f
(
n
)
=
f
(
n
−
1
)
f
(
n
−
2
)
f(n) = f(n-1) + f(n-2)
f(n)=f(n−1)+f(n−2) 然后我们联想到：1 个
2
×
2
2 \times 2
2×2 的矩阵和 1 个
2
×
1
2 \times 1
2×1 的矩阵相乘，得到的还是一个
2
×
1
2 \times 1
2×1 的矩阵；
首先，利用递推公式填充 列向量 和 矩阵 ：
[
f
(
n
)
?
]
=
[
1
1
?
?
]
[
f
(
n
−
1
)
f
(
n
−
2
)
]
\left[ \begin{matrix} f(n) \ ? \end{matrix} \right] = \left[ \begin{matrix} 1 & 1 \ ? & ?\end{matrix} \right] \left[ \begin{matrix} f(n-1) \ f(n-2)\end{matrix} \right]
[f(n)?]=[1?1?][f(n−1)f(n−2)] 接下来利用列向量的传递性把带有问号的列向量补全，得到：
[
f
(
n
)
f
(
n
−
1
)
]
=
[
1
1
?
?
]
[
f
(
n
−
1
)
f
(
n
−
2
)
]
\left[ \begin{matrix} f(n) \ f(n-1)\end{matrix} \right] = \left[ \begin{matrix} 1 & 1 \ ? & ?\end{matrix} \right] \left[ \begin{matrix} f(n-1) \ f(n-2)\end{matrix} \right]
[f(n)f(n−1)]=[1?1?][f(n−1)f(n−2)] 再把带有问号的系数矩阵补全，得到：
[
f
(
n
)
f
(
n
−
1
)
]
=
[
1
1
1
0
]
[
f
(
n
−
1
)
f
(
n
−
2
)
]
\left[ \begin{matrix} f(n) \ f(n-1)\end{matrix} \right] = \left[ \begin{matrix} 1 & 1 \ 1 & 0\end{matrix} \right] \left[ \begin{matrix} f(n-1) \ f(n-2)\end{matrix} \right]
[f(n)f(n−1)]=[1110][f(n−1)f(n−2)] 然后进行逐步化简，得到：
[
f
(
n
)
f
(
n
−
1
)
]
=
[
1
1
1
0
]
[
f
(
n
−
1
)
f
(
n
−
2
)
]
=
[
1
1
1
0
]
[
1
1
1
0
]
[
f
(
n
−
2
)
f
(
n
−
3
)
]
=
[
1
1
1
0
]
⋯
[
1
1
1
0
]
⏟
n
−
1
[
f
(
1
)
f
(
0
)
]
\begin{aligned} \left[ \begin{matrix} f(n) \ f(n-1)\end{matrix} \right] &= \left[ \begin{matrix} 1 & 1 \ 1 & 0\end{matrix} \right] \left[ \begin{matrix} f(n-1) \ f(n-2)\end{matrix} \right] \ &= \left[ \begin{matrix} 1 & 1 \ 1 & 0\end{matrix} \right] \left[ \begin{matrix} 1 & 1 \ 1 & 0\end{matrix} \right] \left[ \begin{matrix} f(n-2) \ f(n-3)\end{matrix} \right] \ &=\underbrace{ \left[ \begin{matrix} 1 & 1 \ 1 & 0\end{matrix} \right] {\cdots}\left[ \begin{matrix} 1 & 1 \ 1 & 0\end{matrix} \right] }_{n-1} \left[ \begin{matrix} f(1) \ f(0)\end{matrix} \right] \ \end{aligned}
[f(n)f(n−1)]=[1110][f(n−1)f(n−2)]=[1110][1110][f(n−2)f(n−3)]=n−1
[1110]⋯[1110][f(1)f(0)] 最后，根据矩阵乘法结合律，把前面的矩阵合并，得到：
[
f
(
n
)
f
(
n
−
1
)
]
=
[
1
1
1
0
]
n
−
1
[
f
(
1
)
f
(
0
)
]
=
A
n
−
1
[
1
0
]
\begin{aligned} \left[ \begin{matrix} f(n) \ f(n-1)\end{matrix} \right] &=\left[ \begin{matrix} 1 & 1 \ 1 & 0\end{matrix} \right]^{n-1}\left[ \begin{matrix} f(1) \ f(0)\end{matrix} \right] \ &=A^{n-1}\left[ \begin{matrix} 1 \ 0 \end{matrix} \right] \end{aligned}
[f(n)f(n−1)]=[1110]n−1[f(1)f(0)]=An−1[10] 于是，只要利用矩阵二分快速幂求得
A
n
−
1
m
o
d
M
A^{n-1} \mod M
An−1modM ，再乘上初始列向量
[
1
0
]
\left[ \begin{matrix} 1 \ 0 \end{matrix} \right]
[10]，得到的列向量的第一个元素就是问题的解了；
事实上，只要列出状态转移方程，当
n
n
n 很大时，我们就可以利用矩阵二分快速幂进行递推式的求解了。
有关矩阵二分的更加深入的内容，可以参考：夜深人静写算法（二十）- 矩阵快速幂。
八、区间DP
有
n
(
n
≤
100
)
n(n \le 100)
n(n≤100) 堆石子摆放成一排，第
i
i
i 堆的重量为
w
i
w_i
wi，现要将石子有次序地合并成一堆。规定每次只能选相邻的二堆合并成新的一堆，合并的消耗为当前合并石子的总重量。试设计出一个算法，计算出将
n
n
n 堆石子合并成一堆的最小消耗。
在思考用动态规划求解的时候，我们可以先想想如果穷举所有方案，会是什么情况。
对于这个问题来说，我们第一个决策可以选择一对相邻石子进行合并，总共有
n
−
1
n-1
n−1 种情况；对于 5堆 石子的情况，第 1 次合并总共有 4 种选择：
- 1）选择 第 1 堆 和 第 2 堆 的石子进行合并，如图所示：
- 2）选择 第 2 堆 和 第 3 堆 的石子进行合并，如图所示：
- 3）选择 第 3 堆 和 第 4 堆 的石子进行合并，如图所示：
- 4）选择 第 4 堆 和 第 5 堆 的石子进行合并，如图所示：
以上任意一种情况都会把石子变成 4 堆，然后就变成了求解
4
4
4 堆石子的问题；我们可以采用同样方法，把石子变成
3
3
3 堆，
2
2
2 堆，最后变成
1
1
1 堆，从而求出问题的最终解。
当然，这是一个递归的过程，每次合并可以将石子堆数减一，总共进行
n
−
1
n-1
n−1 次合并，每个阶段可行的方案数都是乘法的关系，穷举的方案总数就是
(
n
−
1
)
!
(n-1)!
(n−1)!；
例如，上面提到的剩下的这 4 堆石子，采用深度优先搜索枚举所有可行解的搜索树如图所示：
图中用 ‘-’ 表示不同堆石子之间的分隔符，即 1-2-3-4 代表 4 堆的情况，12-3-4表示 第 1 堆 和第 2 堆 合并后的情况。对这么多种方案取总消耗最小的，正确性是一定可以保证的，因为我们枚举了所有情况，然而时间上肯定是无法接受的。
那么，如何来优化搜索呢？我们发现这个问题的难点在于：当选出的两堆石子合并以后，它的重量变成了合并后的和，对于
n
n
n 堆石子，选择的
n
−
1
n-1
n−1 种合并方式，到达的都是不同的状态，无法进行状态存储。
当没有头绪的时候，我们试着将问题反过来思考；我们发现这棵深度优先搜索树的所有叶子结点都是一样的，这就为我们解决问题带来了突破口；对于
[
1
,
n
]
[1, n]
[1,n] 堆石子，假设已经合并了
n
−
2
n-2
n−2 次，必然只剩下 二堆石子，那么我们只需要合并最后一次，就可以把两堆石子变成一堆，假设合并最后一次的位置发生在
k
k
k，也就是最后剩下两堆分别为：
[
1
,
k
]
[1, k]
[1,k] 和
[
k
1
,
n
]
[k+1, n]
[k+1,n]，如图二-2-1所示：
注意，这个时候
[
1
,
k
]
[1, k]
[1,k] 和
[
k
1
,
n
]
[k+1, n]
[k+1,n] 已经各自合并成一堆了，所以我们把问题转换成了求
[
1
,
k
]
[1, k]
[1,k] 合并一堆的最小消耗，以及
[
k
1
,
n
]
[k+1, n]
[k+1,n] 合并成一堆的最小消耗；而这里
k
k
k 的取值范围为
[
1
,
n
−
1
]
[1, n-1]
[1,n−1]；
利用这样的方法，逐步将区间缩小成 1，就可以得到整个问题的解了。令
f
[
i
]
[
j
]
f[i][j]
f[i][j] 表示从 第
i
i
i 堆 石子到 第
j
j
j 堆 石子合并成一堆所花费的最小代价。
f
[
i
]
[
j
]
=
{
0
i
=
j
min
k
=
i
j
−
1
(
f
[
i
]
[
k
]
f
[
k
1
]
[
j
]
c
o
s
t
(
i
,
j
)
)
i
≠
j
f[i][j] = \begin{cases} 0 & i=j\ \min_{k=i}^{j-1}(f[i][k] + f[k+1][j] + cost(i,j)) & i \neq j\end{cases}
f[i][j]={0mink=ij−1(f[i][k]+f[k+1][j]+cost(i,j))i=ji=j
其中
c
o
s
t
(
i
,
j
)
=
∑
k
=
i
j
w
k
cost(i, j) = \sum_{k=i}^{j}w_k
cost(i,j)=∑k=ijwk
有了上面 “正难则反” 的解释，这个状态转移方程就很好理解了；
1）当
i
=
j
i=j
i=j 时，由于
f
[
i
]
[
j
]
f[i][j]
f[i][j] 已经是一堆了，所以消耗自然就是 0 了；
2）当
i
≠
j
i \neq j
i=j 时，我们需要把目前剩下的两堆合并成一堆，一堆是
f
[
i
]
[
k
]
f[i][k]
f[i][k] ，另一堆是
f
[
k
1
]
[
j
]
f[k+1][j]
f[k+1][j]，这两堆合并的消耗就是 从 第
i
i
i 堆到第
j
j
j 堆的重量之和，即
c
o
s
t
(
i
,
j
)
=
∑
k
=
i
j
w
k
cost(i, j) = \sum_{k=i}^{j}w_k
cost(i,j)=∑k=ijwk，而对于合并方案，总共
k
=
j
−
i
k=j-i
k=j−i 种选择，所以枚举
j
−
i
j-i
j−i 次，取其中最小值就是答案了。
通过记忆化搜索求解
f
[
1
]
[
n
]
f[1][n]
f[1][n] 就是最后的答案。
如图所示的动图，展示的是迭代求解的顺序，灰色的格子代表无效状态，红色的格子代表为长度为 2 的区间，橙色的格子代表为长度为 3 的区间，金黄色的格子则代表长度为 4 的区间，黄色的格子代表我们最终要求的区间状态，即
f
[
1
]
[
5
]
f[1][5]
f[1][5]。
有关区间DP的更深入内容，可以参考：夜深人静写算法（二十七）- 区间DP。
九、数位DP
如果一个数的所有位数加起来是
10
10
10 的倍数, 则称之为
g
o
o
d
n
u
m
b
e
r
good \ number
good number，求区间
[
l
,
r
]
(
0
≤
l
≤
r
≤
1
0
18
)
[l, r](0 \le l \le r \le 10^{18})
l,r 内
g
o
o
d
n
u
m
b
e
r
good \ number
good number 的个数；
对于这个问题，朴素算法就是枚举区间里的每个数，并且判断可行性，时间复杂度为
o
(
(
r
−
l
)
c
)
o((r-l)c)
o((r−l)c)，
c
=
19
c=19
c=19，肯定是无法接受的。
对于区间
[
l
,
r
]
[l, r]
[l,r] 内求满足数量的数，可以利用差分法分解问题；
假设
[
0
,
x
]
[0, x]
[0,x] 内的
g
o
o
d
n
u
m
b
e
r
good \ number
good number 数量为
g
x
g_x
gx，那么区间
[
l
,
r
]
[l, r]
[l,r] 内的数量就是
g
r
−
g
l
−
1
g_r - g_{l-1}
gr−gl−1；分别用同样的方法求出
g
r
g_r
gr 和
g
l
−
1
g_{l-1}
gl−1，再相减即可；
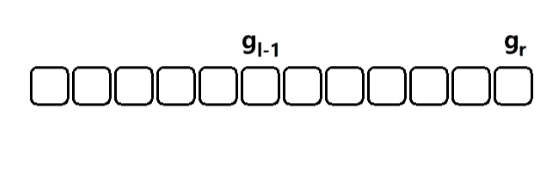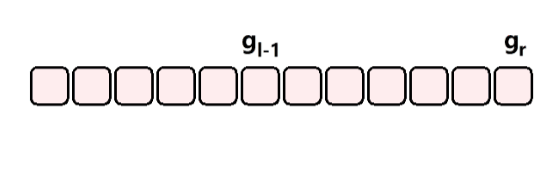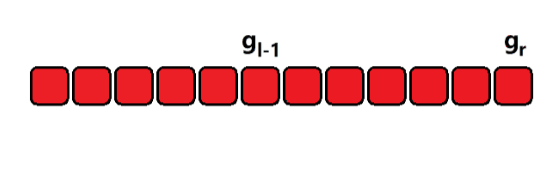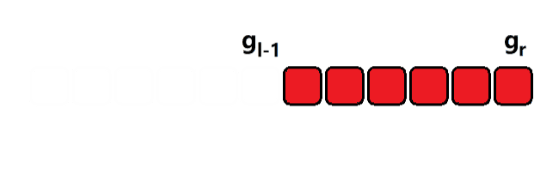
如果一个数字
i
i
i 满足
i
<
x
i < x
i<x，那么
i
i
i 从高到低肯定出现某一位，使得这一位上的数值小于
x
x
x 对应位上的数值，并且之前的所有高位都和
x
x
x 上的位相等。
举个例子，当
x
=
1314
x = 1314
x=1314 时，
i
=
0
a
b
c
i=0abc
i=0abc、
i
=
12
a
b
i=12ab
i=12ab、
i
=
130
a
i=130a
i=130a、
i
=
1312
i=1312
i=1312，那么对于
i
i
i 而言，无论后面的字母取什么数字，都是满足
i
<
x
i < x
i<x 这个条件的。
如果我们要求
g
1314
g_{1314}
g1314 的值，可以通过枚举高位：当最高位为0，那么问题就转化成
g
999
g_{999}
g999 的子问题；当最高位为1，问题就转化成
g
314
g_{314}
g314 的子问题。
g
314
g_{314}
g314 可以继续递归求解，而
g
999
g_{999}
g999 由于每一位数字范围都是
[
0
,
9
]
[0,9]
[0,9]，可以转换成一般的动态规划问题来求解。
这里的前缀状态就对应了之前提到的 某些条件；
在这个问题中，前缀状态的描述为：一个数字前缀的各位数字之和对10取余（模）的值。前缀状态的变化过程如图所示：
在上题中，前缀状态的含义是：对于一个数 520 ，我们不需要记录 520 ，而只需要记录 7；对于 52013，我们不需要记录 52013，而只需要记录 1。这样就把原本海量的状态，变成了最多 10 个状态。
根据以上的三个信息，我们可以从高位到低位枚举数字
i
i
i 的每一位，逐步把问题转化成小问题求解。
我们可以定义
f
(
n
,
s
t
,
l
i
m
)
f(n, st, lim)
f(n,st,lim) 表示剩下还需要考虑
n
n
n 位数字，前面已经枚举的高位组成的前缀状态为
s
t
st
st，且用
l
i
m
lim
lim 表示当前第
n
n
n 位是否能够取到最大值（对于
b
b
b 进制，最大值就是
b
−
1
b-1
b−1，比如 10 进制状态下，最大值就是 9） 时的数字个数。我们来仔细解释一下这三维代表的含义：
- 1）当前枚举的位是
n
n
n 位，
n
n
n 大的代表高位，小的代表低位；
- 2）
s
t
st
st 就是前缀状态，在这个问题中，代表了所有已经枚举的高位（即数字前缀）的各位数字之和对10取余（模）。注意：我们并不关心前缀的每一位数字是什么，而只关心它们加和模10之后的值是什么。
- 3）
l
i
m
=
t
r
u
e
lim=true
lim=true 表示的是已经枚举的高位中已经出现了某一位比给定
x
x
x 对应位小的数，那么后面枚举的每个数最大值就不再受
x
x
x 控制；否则，最大值就应该是
x
x
x 的对应位。举例说明，当十进制下的数
x
=
1314
x = 1314
x=1314 时，枚举到高位前三位为 “131”，
l
i
m
=
f
a
l
s
e
lim = false
lim=false， 那么第四位数字的区间取值就是
[
0
,
4
]
[0,4]
[0,4]；而枚举到高位前三位为 “130” 时，
l
i
m
=
t
r
u
e
lim = true
lim=true，那么第四位数字的区间取值就是
[
0
,
9
]
[0, 9]
[0,9]。
所以，我们根据以上的状态，预处理
x
x
x 的每个数位，表示成十进制如下：
x
=
d
n
d
n
−
1
.
.
.
d
1
x = d_nd_{n-1}…d_1
x=dndn−1…d1 (其中
d
n
d_n
dn 代表最高位，
d
1
d_1
d1 代表最低位)
得出状态转移方程如下：
f
(
n
,
s
t
,
l
i
m
)
=
∑
k
=
0
m
a
x
v
f
(
n
−
1
,
(
s
t
k
)
m
o
d
10
,
l
i
m
o
r
(
k
<
m
a
x
v
)
)
\begin{aligned}& f(n, st, lim) \ &= \sum_{k=0}^{maxv} f(n-1, (st+k) \mod 10, lim \ or \ (k < maxv))\end{aligned}
f(n,st,lim)=k=0∑maxvf(n−1,(st+k)mod10,lim or (k<maxv))
k
k
k 表示第
n
n
n 位取什么数字，它的范围是
[
0
,
m
a
x
v
]
[0, maxv]
[0,maxv]；
m
a
x
v
maxv
maxv 表示第
n
n
n 位能够取到的最大值，它由
l
i
m
lim
lim 决定，即：
m
a
x
v
=
{
9
l
i
m
=
t
r
u
e
d
n
l
i
m
=
f
a
l
s
e
maxv = \begin{cases}9 & lim = true\d_n & lim = false\end{cases}
maxv={9dnlim=truelim=false
利用上述的状态转移方程，我们可以进行递归求解，并且当
n
=
0
n=0
n=0 的时候为递归出口，由于数字要求满足所有数字位数之和为
10
10
10 的倍数，所以只有
s
t
=
0
st = 0
st=0 的情况为合法状态，换言之，当
n
=
0
n=0
n=0 时，有：
f
(
0
,
x
,
l
i
m
)
=
{
1
x
=
0
0
0
<
x
≤
9
f(0, x, lim) = \begin{cases} 1 & x = 0\ 0 & 0 \lt x \le 9\end{cases}
f(0,x,lim)={10x=00<x≤9 而我们需要求的，就是
f
(
n
,
0
,
f
a
l
s
e
)
f(n, 0, false)
f(n,0,false)。
我们发现，如果按照以上的状态转移进行求解，会导致一个问题，就是会有很多重叠子问题，所以需要进行记忆化，比较简单的方法就是用一个三维数组
f
[
n
]
[
s
t
]
[
l
i
m
]
f[n][st][lim]
f[n][st][lim] 来记忆化。
当然，这里有一个技巧，就是
l
i
m
lim
lim 这个变量只有
t
r
u
e
true
true、
f
a
l
s
e
false
false 两种取值，并且当它为
f
a
l
s
e
false
false 时，代表之前枚举的数的高位和所求区间
[
0
,
x
]
[0, x]
[0,x] 右端点中的
x
x
x 的高位保持完全一致，所以当
l
i
m
=
f
a
l
s
e
lim = false
lim=false 时，深度优先搜索树的分支最多只有
1
1
1 条，所以无须记忆化，每次直接算就可以。如图二-3-2所示的蓝色结点，就是那条唯一分支。
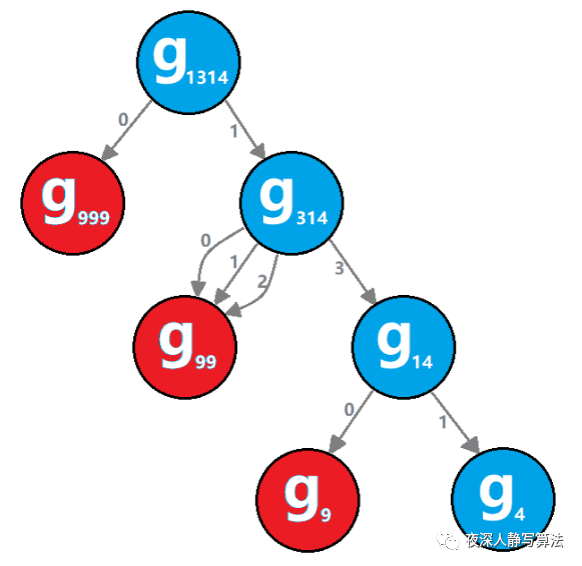
综上所述，我们只需要用
f
[
n
]
[
s
t
]
f[n][st]
f[n][st] 表示长度为
n
n
n，且每个数字的范围为
[
0
,
m
a
x
v
]
[0, maxv]
[0,maxv]，且前缀状态为
s
t
st
st 的数字个数（这里
m
a
x
v
maxv
maxv 和进制有关，如果是
b
b
b 进制，那么
m
a
x
v
=
b
−
1
maxv = b - 1
maxv=b−1）。
- f
(
n
,
s
t
,
f
a
l
s
e
)
f(n, st, false)
f(n,st,false) 采用普通深搜，
f
(
n
,
s
t
,
t
r
u
e
)
f(n, st, true)
f(n,st,true) 采用记忆化搜索。
对于更加深入的数位DP的实现，可以参考：夜深人静写算法（二十九）- 数位DP。
十、状态压缩DP
给出
g
r
a
p
h
graph
graph 为有
n
(
n
≤
12
)
n(n \le 12)
n(n≤12) 个节点（编号为 0, 1, 2, …,
n
−
1
n-1
n−1）的无向连通图。
g
r
a
p
h
.
l
e
n
g
t
h
=
n
graph.length = n
graph.length=n，且只有节点
i
i
i 和
j
j
j 连通时，
j
j
j 不等于
i
i
i 时且在列表
g
r
a
p
h
[
i
]
graph[i]
graph[i] 中恰好出现一次。返回能够访问所有节点的最短路径的长度。可以在任一节点 开始 和 结束，也可以多次重访节点，并且可以重用边。
这是一个可重复访问的 旅行商问题。我们可以设计状态如下：
f
(
s
t
,
e
n
,
s
t
a
t
e
)
f(st, en, state)
f(st,en,state) 代表从
s
t
st
st 到
e
n
en
en，且 经过的节点 的状态组合为
s
t
a
t
e
state
state 的最短路径。
状态组合的含义是：经过二进制来压缩得到的一个数字，比如 经过的节点 为 0、1、4，则
s
t
a
t
e
state
state 的二进制表示为：
(
10011
)
2
(10011)_2
(10011)2 即 经过的节点 对应到状态
s
t
a
t
e
state
state 二进制表示的位为 1，其余位为 0。
于是，我们明确以下几个定义：初始状态、最终状态、非法状态、中间状态。
初始状态
初始状态 一定是我们确定了某个起点，想象一下，假设起点在
i
i
i，那么在一开始的时候，必然
s
t
a
t
e
=
2
i
state = 2^i
state=2i。于是，我们可以认为起点在
i
i
i，终点在
i
i
i，状态为
2
i
2^i
2i 的最短路径为 0。也就是初始状态表示如下：
f
(
i
,
i
,
2
i
)
=
0
i
∈
[
0
,
n
)
f(i, i, 2^i) = 0 \ \ \ i \in [0, n)
f(i,i,2i)=0 i∈[0,n)
最终状态
由于这个问题，没有告诉我们 起点 和 终点，所以 起点 和 终点 是不确定的，我们需要通过枚举来得出，所以最终状态 起点
i
i
i 和 终点
j
j
j，状态为
2
n
−
1
2^n-1
2n−1（代表所有点都经过，二进制的每一位都为 1）。最终状态表示为：
f
(
i
,
j
,
2
n
−
1
)
i
∈
[
0
,
n
)
,
j
∈
[
0
,
n
)
f(i, j, 2^n-1) \ \ \ i \in [0, n), j \in [0, n)
f(i,j,2n−1) i∈[0,n),j∈[0,n)
非法状态
非法状态 就是 不可能从初始状态 通过 状态转移 到达的状态。我们设想一下，如果
f
(
i
,
j
,
s
t
a
t
e
)
f(i, j, state)
f(i,j,state) 中
s
t
a
t
e
state
state 的二进制的第
i
i
i 位为 0，或者第
j
j
j 位 为 0，则这个状态必然是非法的，它代表了两个矛盾的对立面。
我们把非法状态下的最短路径定义成
i
n
f
=
10000000
inf = 10000000
inf=10000000 即可。
f
(
i
,
j
,
s
t
a
t
e
)
=
i
n
f
f(i, j, state) = inf
f(i,j,state)=inf
其中 (state & (1<<i)) == 0或者(state & (1<<j)) == 0代表state的二进制表示的第
i
i
i 和
j
j
j 位没有 1。
中间状态
除了以上三种状态以外的状态，都成为中间状态。
那么，我们可以通过 记忆化搜索，枚举所有的
f
(
i
,
j
,
2
n
−
1
)
f(i, j, 2^n - 1)
f(i,j,2n−1) 的，求出一个最小值就是我们的答案了。状态数：
O
(
n
2
2
n
)
O(n22n)
O(n22n)，状态转移：
O
(
n
)
O(n)
O(n)，时间复杂度：
O
(
n
3
2
n
)
O(n32n)
O(n32n)。
十一、斜率DP
给定
n
(
n
≤
400000
)
n(n \le 400000)
n(n≤400000) 个数
a
n
a_n
an，现在需要将它们归类，每类至少
t
(
1
<
t
≤
n
)
t(1 < t \le n)
t(1<t≤n) 个数。归在同一类的花费为每个数字减去最小那个数字之和。希望所有数归类后的总花费最小，求这个最小花费。
首先贪心，排个序先。然后用
s
u
m
[
i
]
sum[i]
sum[i] 代表前
i
i
i 个数的和，其中
s
u
m
[
0
]
=
0
sum[0]=0
sum[0]=0，
d
p
[
i
]
dp[i]
dp[i] 代表前
i
i
i 个数字归完类后的最小花费，则容易列出状态转移方程：
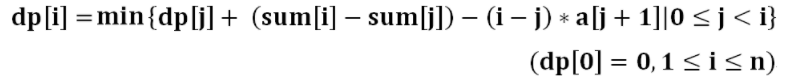
因为是排好序的，所以
a
[
j
1
]
a[j+1]
a[j+1] 是
a
[
j
1
:
i
]
a[j+1:i]
a[j+1:i] 这个区间内最小的那个数，这是个
1
D
/
1
D
1D/1D
1D/1D 问题，即状态数为
O
(
n
)
O(n)
O(n)，每个状态的转移成本为
O
(
n
)
O(n)
O(n)，所以总的算法复杂度为
O
(
n
2
)
O(n^2)
O(n2)。朴素算法如下：
由于
n
n
n 的范围太大，需要优化。算法优化的本质就是让上述代码的第一层循环不变，减少第二层循环的状态转移过程。首先将状态转移方程进行移项，得到如下等式：
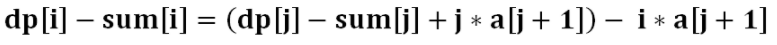
看上去貌似并没有什么变化，这么做的目的是什么呢？再来仔细看下这个式子：
这样一看，基本上就能看懂分类依据了，红色代表自变量为i的函数，绿色代表自变量为j的函数，蓝色则是以
i
i
i 和
j
j
j 为变量的函数，那么我们做进一步转化，使得该公式更加清晰。
将
i
i
i 和
j
j
j 为自变量的函数分别用b和y表示，
k
=
i
k=i
k=i 代表斜率。于是，状态转移方程转化成了以
a
[
j
1
]
a[j+1]
a[j+1] 为自变量，
i
i
i 为斜率，
d
p
[
i
]
−
s
u
m
[
i
]
dp[i]-sum[i]
dp[i]−sum[i] 为截距的直线方程。
如上图所示，当
i
i
i 确定，
j
j
j 取
t
t
t 时，则代表的是一条斜率为
i
i
i，并且过点
T
(
a
[
t
1
]
,
d
p
[
t
]
−
s
u
m
[
t
]
t
∗
a
[
t
1
]
)
T(a[t+1], dp[t]-sum[t]+t*a[t+1])
T(a[t+1],dp[t]−sum[t]+t∗a[t+1]) 的直线。
更加一般地，当
i
i
i 确定，
j
j
j 取不同值时，则这个平面上会出现一系列平行的直线，他们的斜率都是
i
i
i。因为
i
i
i 是确定的，并且所有直线的斜率就是
i
i
i，所以所有直线相互平行；又由于
j
j
j 的不同，直线经过不同的点，所以只要是两条不重合的平行直线，截距必然不同，而截距
b
=
d
p
[
i
]
−
s
u
m
[
i
]
b=dp[i]-sum[i]
b=dp[i]−sum[i]，即
d
p
[
i
]
=
b
s
u
m
[
i
]
dp[i]=b+sum[i]
dp[i]=b+sum[i]；所以可以得出结论：
dp[i]的最小值一定出现在最下面的那条直线上（因为最下面的直线截距最小）。
接下来，我们分析几条比较重要的性质：
第一条：维护“下凸”折线
如图所示，A、B、C三个点，其中B点位于AC直线之上，即为一个“上凸”点。然后我们连接AC两点，绘制所有的斜率小于K(A,C)的直线（图中绿色直线），发现截距最小的一定是经过点A的直线（想象一下，图中三根绿色的直线一起动起来的情况）；然后绘制所有的斜率大于K(A,C)的直线（图中红色直线），发现截距最小的一定是经过C的直线。于是，可以得出结论，在用A、B、C进行状态转移时，B永远是一个无用的状态转移。
由于任意三点不能出现“上凸”。所以，所有用于状态转移的点必须是一条“下凸”折线，如图所示：
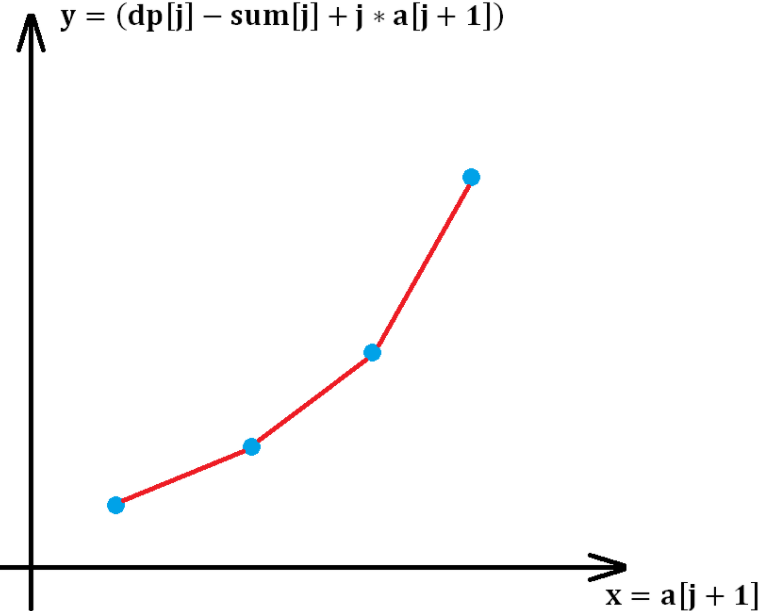
图中每个点都代表了向dp[i]进行状态转移的dp[j]。从图中可以看出，“下凸”折线满足每段折线斜率单调递增。那么如何维护这段“下凸”折线？
我们采用双端队列来维护，由于它存储结构的单调性（斜率单调），又称为“单调队列”。deq[]代表单调队列的数据域，head和tail分别表示它的两个指针，当 head和tail相等则代表单调队列为空，初始化head=tail=0。deq[]中的每个元素存的是原数组的下标，因为通过下标就能计算出坐标图中点的 x-y坐标，也就能计算相邻两点之间的斜率了。
那么每次我们将一个可行的转移状态j放入单调队列之前，先判断它的加入能否保证斜率单调递增，如果不能则将单调队列尾元素删除，依次往复，最后将这个点放入单调队列尾部，这样一条“下凸”折线就算维护完毕了。
细心的读者，会发现这一步操作同样可以用“栈”这种数据结构来完成。接下来，我们继续来探讨为什么用双端队列不用栈。
第二条：“永不录用”点的剔除
“永不录用”这个名字是我自己起的，那么哪些点是“永不录用”点？，还是来看图：
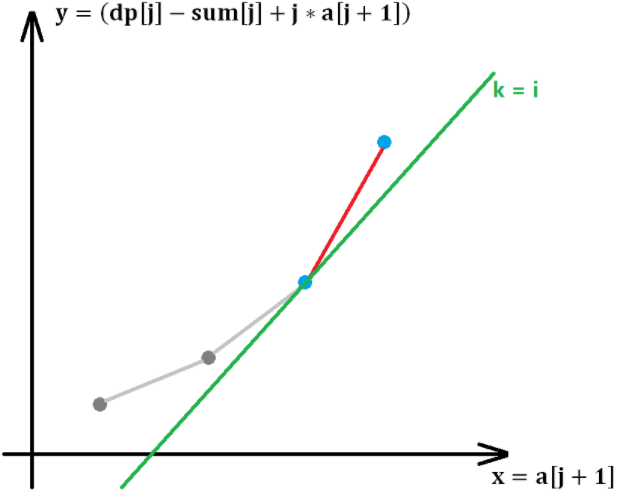
由于每次枚举状态i时是递增的枚举（之前那段代码的第一个for循环），也就是说斜率一定是越来越大，那么从图中可以看出，那些斜率小于i的折线上的点（灰色点）如果要经过斜率为i的直线（图中绿色直线的平行线），则产生的截距必然不会比图中绿色直线的更小，也就是灰色点都可以删除了。
这些可以删除的灰色点就是“永不录用”点。“永不录用”点更加官方的说法，就是单调队列里的折线中，所有斜率小于i的折线的左端点。由于单调队列的斜率单调性，所以删除点的操作可以从左往右进行，这就是为什么之前不用栈来维护的根本原因。如果维护折线用的是栈，则最左边的点势必在栈底，而栈这种数据结构只能获取栈顶元素。
十二、连通性DP
我觉得你应该也看不到这里，如果你看到了这里，那请在评论区说一句：“我看到了！”。那我只能说：草率了。
这应该是 ACM 中最难的动态规划问题了，所以我打算专门拿一篇文章来讲它，放心吧，职场面试一定不会考，如果考到了，那么面试官一定是想秀一下演技。
关于 「 动态规划 」 的内容到这里就结束了。
如果还有不懂的问题，可以通过 「 电脑版主页 」找到作者的「 联系方式 」 ，线上沟通交流。
有关🌳《画解数据结构》🌳 的源码均开源，链接如下：《画解数据结构》
相信看我文章的大多数都是**「 大学生 」，能上大学的都是「 精英 」，那么我们自然要「 精益求精 」，如果你还是「 大一 」，那么太好了，你拥有大把时间，当然你可以选择「 刷剧 」，然而，「 学好算法 」，三年后的你自然「 不能同日而语 」。
那么这里，我整理了「 几十个基础算法 」** 的分类，点击开启：
如果链接被屏蔽，或者有权限问题，可以私聊作者解决。
🔥让天下没有难学的算法🔥
C语言免费动漫教程，和我一起打卡！
入门级C语言真题汇总
几张动图学会一种数据结构
组团学习，抱团生长
竞赛选手金典图文教程
粉丝专属福利
语言入门：《光天化日学C语言》(示例代码)
语言训练：《C语言入门100例》试用版
数据结构：《画解数据结构》源码
算法入门：《算法入门》指引
算法进阶：《夜深人静写算法》算法模板
👇🏻
验证码 可通过搜索下方
公众号 获取👇🏻
感谢每一个认真阅读我文章的人，看着粉丝一路的上涨和关注，礼尚往来总是要有的：
① 2000多本Python电子书（主流和经典的书籍应该都有了）
② Python标准库资料（最全中文版）
③ 项目源码（四五十个有趣且经典的练手项目及源码）
④ Python基础入门、爬虫、web开发、大数据分析方面的视频（适合小白学习）
⑤ Python学习路线图（告别不入流的学习）
网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。
一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
