【最小二乘算法】含有遗忘因子的最小二乘算法的永磁同步电机PMSM在线转动惯量和阻尼系数辨识

梦想科研社

于 2024-11-14 13:45:00 发布

阅读量555

点赞数 9

文章标签：算法

本文链接：https://blog.csdn.net/2401_84610415/article/details/143717121

版权

摘要

本文提出了一种基于含有遗忘因子的最小二乘算法的在线辨识方法，用于永磁同步电机（PMSM）转动惯量和阻尼系数的辨识。通过在控制系统中引入遗忘因子，增强了算法对实时变化的响应能力。仿真结果验证了所提方法的有效性与精度。

理论

永磁同步电机数学模型永磁同步电机（PMSM）的动态数学模型可描述为：

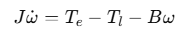
其中：

𝐽为转动惯量
𝜔为角速度
𝑇𝑒 为电磁转矩
𝑇𝑙为负载转矩
𝐵为阻尼系数

2. 最小二乘算法 最小二乘法通过最小化误差平方和来估计模型参数，基本更新公式为：

其中：

𝐾 ( 𝑘 ) 为增益矩阵
𝜙 ( 𝑘 ) 为回归矩阵
𝑦 ( 𝑘 ) 为系统输出

3. 引入遗忘因子

为了增强算法对动态变化的跟踪能力，引入遗忘因子𝜆 ，更新公式为：

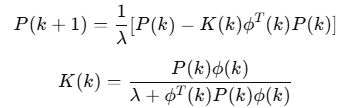
实验结果

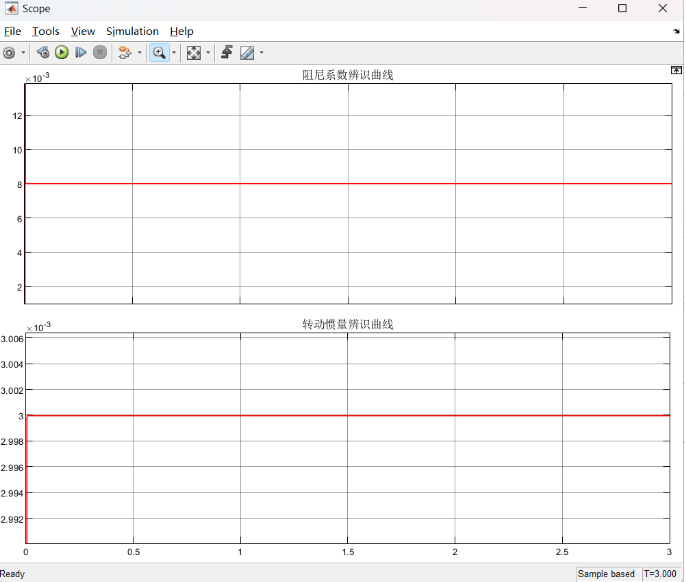
1. 参数辨识曲线

图1显示了转动惯量𝐽和阻尼系数 𝐵的在线辨识结果，辨识值逐渐趋于稳定。

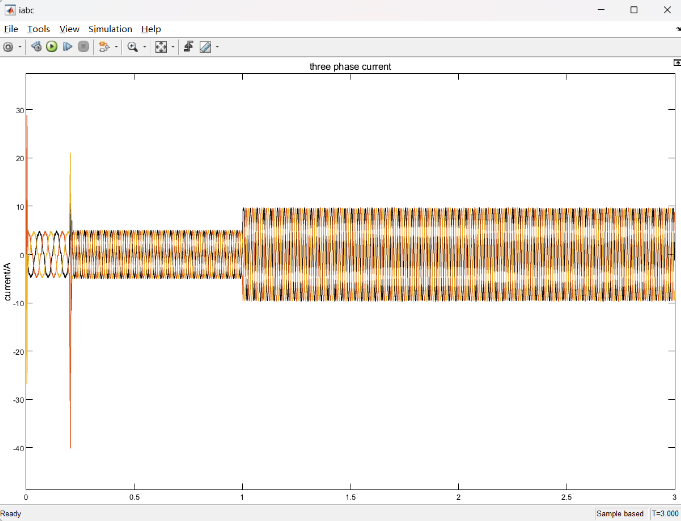
2. 电机电流波形

图2展示了三相电流波形，控制系统能够在较短时间内达到稳态，表明辨识方法对控制精度的改善。

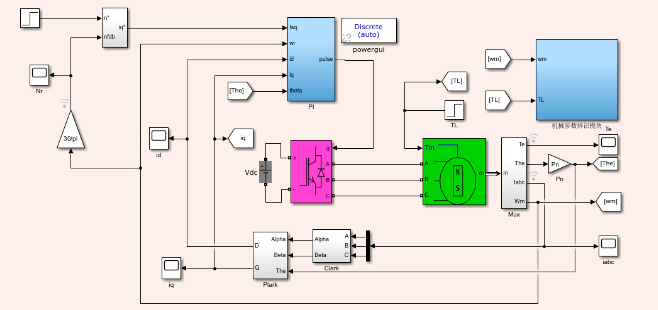
3. 系统框图

图3为永磁同步电机控制系统的Simulink框图，展示了整个辨识与控制过程。

部分代码

% PMSM参数辨识最小二乘算法
lambda = 0.98; % 遗忘因子
P = eye(2);    % 初始协方差矩阵
theta = [0; 0]; % 参数初值 [J; B]

for k = 1:length(data)
    phi = [current_data(k); velocity_data(k)];
    y = torque_data(k);
    K = P * phi / (lambda + phi' * P * phi);
    theta = theta + K * (y - phi' * theta);
    P = (P - K * phi' * P) / lambda;
    
    J_est(k) = theta(1);
    B_est(k) = theta(2);
end

% 结果绘图
plot(time, J_est, 'r', time, B_est, 'b');
xlabel('Time (s)');
ylabel('Parameters');
legend('J (Inertia)', 'B (Damping)');

参考文献

❝

Ljung, L. (1999). System Identification: Theory for the User. Prentice Hall.

Chen, H., & Zhang, J. (2015). Online Parameter Estimation for PMSM Using Recursive Least Squares Algorithm. IEEE Transactions on Energy Conversion.

Zhao, S., & Li, X. (2020). Adaptive Control of PMSM with Online Parameter Identification. IEEE Transactions on Industrial Electronics.

（文章内容仅供参考，具体效果以图片为准）