笔记3 使用SPSS进行主成分分析

最新推荐文章于 2025-05-12 11:08:18 发布

小雨的笔记

最新推荐文章于 2025-05-12 11:08:18 发布

阅读量761

点赞数 12

文章标签：人工智能

本文链接：https://blog.csdn.net/2401_84631166/article/details/146129383

版权

试利用主成分综合评价全国各地区水泥制造业规模以上企业的经济效益，原始数据来源于 2014年《中国水泥统计年鉴》，如表1所示。

表 1 2013年各地区水泥制造业规模以上企业的主要经济指标

地区	企业单位数（个）	流动资产合计（亿元）	资产总额（亿元）	负债总额（亿元）	主营业务收入（亿元）	利润总额（亿元）	销售利润率（%）
北京	8	17.6	43.8	17.8	26.6	-1.4	-5.2
天津	24	43.8	91.7	33.7	35.9	1.5	4.1
河北	231	281.4	993.8	647	565.1	22.7	4
山西	113	103.4	317.4	238.5	124	-2.1	-1.7
内蒙古	116	135.9	384.4	256.8	245.8	11.9	4.8
辽宁	151	151.4	417.6	247.9	350.3	23	6.6
吉林	69	333.7	627.7	415.2	539.8	25.4	4.7
黑龙江	96	142.1	331.6	234.7	183.2	13.5	7.4
上海	14	21.5	28.3	12.6	31.6	1.2	4
江苏	254	300.3	680	435.7	713.3	62.6	8.8
浙江	192	259.8	561.9	300.1	473.9	42.1	8.9
安徽	169	217.2	591.9	305.2	518.8	64.9	12.5
福建	111	93.2	276.4	163.9	284.8	11.2	3.9
江西	138	143.8	398.1	208.4	400.3	47.5	11.9
山东	295	351.8	792.7	412.5	878.3	80.3	9.1
河南	238	388.5	804.2	475.2	673.7	58.3	8.7
湖北	151	193	619.7	360.7	570.5	49.1	8.6
湖南	220	86.4	398.8	212.3	434.1	33.6	7.7
广东	204	217	592.1	345.3	474.3	40.5	8.5
广西	148	116	387.2	178.7	344	49.6	14.4
海南	15	53.1	102.1	52.9	80.7	5.6	6.9
重庆	78	158.3	419.8	294.1	185.1	8.4	4.5
四川	196	218.2	739.1	433.3	465.2	37.1	8
贵州	133	91.5	367.5	244.2	224.7	28.2	12.6
云南	149	134.2	434.7	290.2	251	11.3	4.5
西藏	10	11.3	26.5	5.4	17.4	4.1	23.7
陕西	116	82.2	312.6	203.8	253.2	14.4	5.7
甘肃	68	61.8	213.2	126.8	124.3	13.3	10.7
青海	20	39.5	152.7	123.1	44.4	3	6.7

对数据进行主成分分析

将上表中的数据录入 SPSS数据表，对数据进行标准化，选择从相关阵对数据做主成分分析。依次点选Analyze->Dimension Reduction->Factor，进入 Factor Analysis 对话框，将7个指标变量选入 Variables 框中。

然后点击右侧的 Descriptives 按钮，在弹出的对话框中，在 Correlation Matrix 中选择 Coefficients，KMO and Bartlett's test ofsphericity。

在Extraction对话框中，在Display选择scree plot

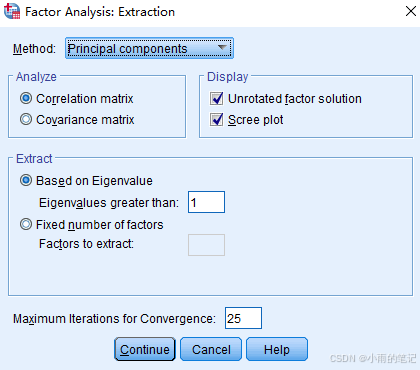
对输出结果进行分析

首先对数据进行KMO and Bartlett's test ofsphericity检验和相关阵的计算，经检验可知：KMO and Bartlett's test ofsphericity检验结果为0.785大于0.05，不拒绝原假设，并且样本相关阵中相关系数较高，说明8个变量具有很强相关性，可以进行主成分分析。