垂直涡度方程推导

最新推荐文章于 2025-03-20 10:42:24 发布

2401_85467005

最新推荐文章于 2025-03-20 10:42:24 发布

阅读量248

点赞数 9

文章标签：算法人工智能机器学习

本文链接：https://blog.csdn.net/2401_85467005/article/details/145388529

版权

为避免遗忘以及巩固之前学过的内容，所以想要写篇文章记录一下之前学过的大气涡度方程推导。

关于推导垂直涡度方程之前要知道两个前提，一个是x方向上的流体运动方程；一个是y方向上的流体运动方程。

这两个方程取自流体力学中气体定常流动中的连续性方程。

这里顺便说一下这两个公式是怎么推导出来的。举一个例子，如下图有一个通道，流体从左往右流动。设左边为流进的流体面A1，右边为流出的流体面A2。

$- \int_{A1}^{} \rho VndA=\int_{A2}^{}\rho VndA$

$\Rightarrow \rho 1V1A1=\rho 2V2A2$

$\Rightarrow \rho 1=\rho 2$

$\Rightarrow V1A1=V2A2$

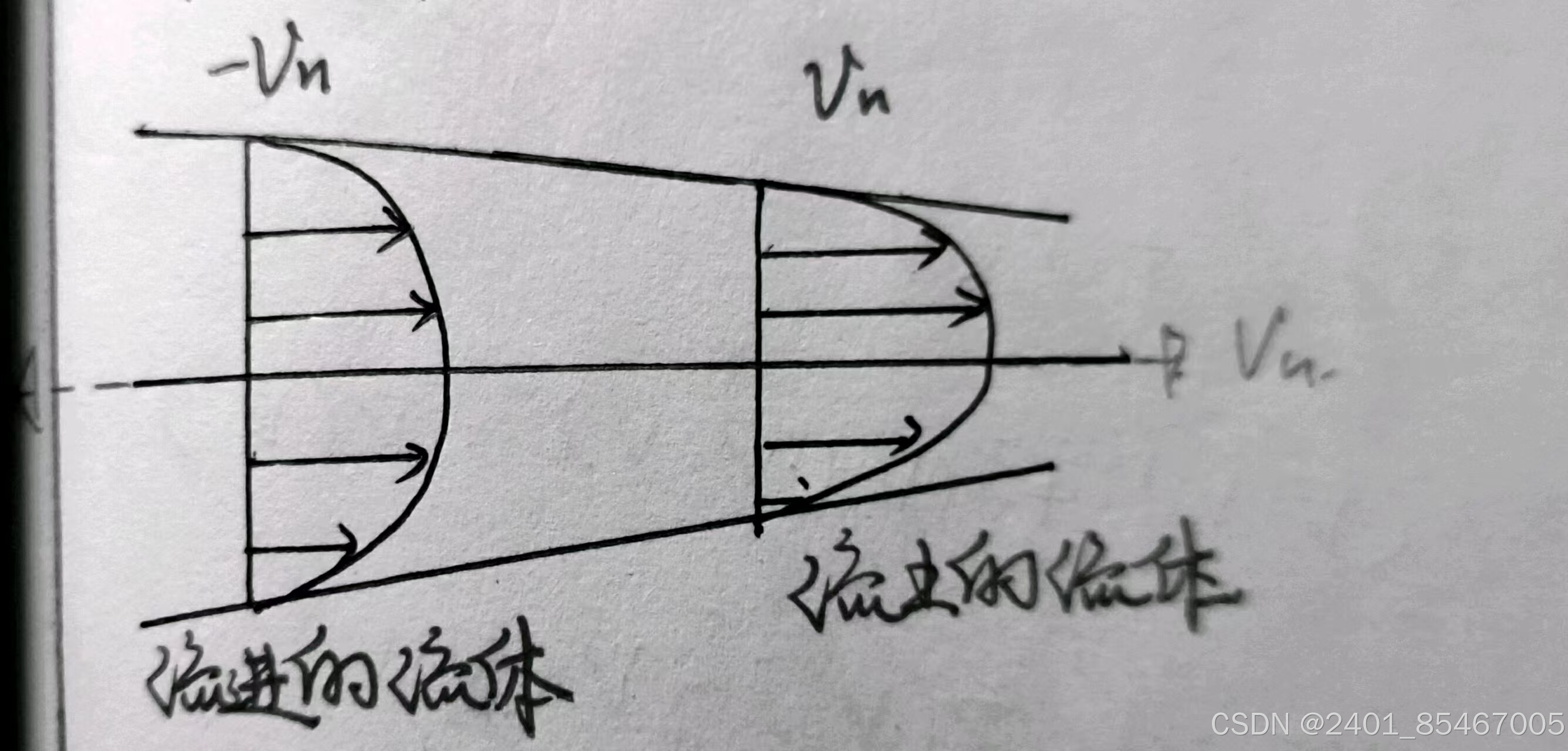
根据动量定理建立微分方程（欧拉运动）

$\frac{d}{dt}(mv)=F$

$\frac{d}{dt} (\rho V v)=F$

$\rho f x \Delta x \Delta y \Delta z +(p-\frac{\delta p}{\delta x})\frac{\delta x}{2}\delta y \delta z - (p+\frac{\delta p}{\delta x}\frac{\delta x}{2})\delta y \delta z=F$

$\rho fx\Delta x \Delta y \Delta z-\frac{\delta p}{\delta x}{\Delta x}\Delta y\Delta z= F$

代入上面

$\frac{d}{dt}(\rho Vv)= F$

从而

$\frac{d}{dt}(\rho Vv)=\rho fx\Delta x \Delta y \Delta z-\frac{\delta p}{\delta x}{\Delta x}\Delta y\Delta z$

$\frac{d}{dt}(\rho v)=\rho fx-\frac{\delta p}{\delta x}$

将该方程展开即可得下面x方向上的运动方程。y方向上的运动方程可依同理求得。

$\large{\frac{\delta u}{\delta t}+u\frac{\delta u}{\delta y}+v\frac{\delta u}{\delta y}+w\frac{\delta u}{\delta z}-fv=-\frac{1}{\rho }\frac{\delta P}{\delta x}+Fx }$ (1)

$\large{\frac{\delta V}{\delta t}+u\frac{\delta V}{\delta y}+v\frac{\delta V}{\delta y}+w\frac{\delta V}{\delta z}-fv=-\frac{1}{\rho }\frac{\delta P}{\delta x}+Fy}$ (2)

由(1)x方向的流体方程对y求偏导,左边可得：

$\large{\frac{\delta u}{\delta t}+u\frac{\delta u}{\delta x}+v\frac{\delta u}{\delta y}+w\frac{\delta u}{\delta z}-fv\Rightarrow\frac{\delta^{2} u}{\delta t\delta y}+\frac{\delta u}{\delta x}\frac{\delta u}{\delta y}+u\frac{\delta^{2} u}{\delta x\delta y}+\frac{\delta v}{\delta y} \frac{\delta u}{\delta y}+v\frac{\delta^{2} u}{\delta y^{2}}+\frac{\delta w}{\delta y}\frac{\delta u}{\delta z}+w\frac{\delta^{2}u}{\delta z\delta y}-\frac{\delta f}{\delta y}v-f\frac{\delta v}{\delta y}}$

右边可得：

$-\frac{1}{\rho }\frac{\delta P}{\delta x}+Fx \Rightarrow -\frac{\delta(\frac{1}{\rho })}{\delta y}\frac{\delta p}{\delta x}-\frac{1}{\rho }\frac{\delta^{2}}{\delta x \delta y}+\frac{\delta Fx}{\delta y}\Rightarrow\frac{1}{\rho ^{2}}\frac{\delta \rho }{\delta y}\frac{\delta p}{\delta x}-\frac{1}{\rho }\frac{\delta^{2}}{\delta x \delta y}+\frac{\delta Fx}{\delta y}$

从而可得(3)式：

$\frac{\delta^{2} u}{\delta t\delta y}+\frac{\delta u}{\delta x}\frac{\delta u}{\delta y}+u\frac{\delta^{2} u}{\delta x\delta y}+\frac{\delta v}{\delta t} \frac{\delta u}{\delta y}+v\frac{\delta^{2} u}{\delta y^{2}}+\frac{\delta w}{\delta y}\frac{\delta u}{\delta z}+w\frac{\delta^{2}u}{\delta z\delta y}-\frac{\delta f}{\delta y}v-f\frac{\delta v}{\delta y}=\frac{1}{\rho ^{2}}\frac{\delta \rho }{\delta y}\frac{\delta p}{\delta x}-\frac{1}{\rho }\frac{\delta^{2}}{\delta x \delta y}+\frac{\delta Fx}{\delta y}$

由(2)y方向的流体方程对x求偏导，左边可得：

$\large{\frac{\delta V}{\delta t}+u\frac{\delta V}{\delta x}+v\frac{\delta V}{\delta y}+w\frac{\delta V}{\delta z}-fv\Rightarrow\frac{\delta^{2} V}{\delta t\delta x}+\frac{\delta u}{\delta x}\frac{\delta V}{\delta x}+u\frac{\delta^{2} V}{\delta x^{2}}+\frac{\delta V}{\delta x} \frac{\delta V}{\delta y}+v\frac{\delta^{2} V}{\delta y\delta x}+\frac{\delta w}{\delta x}\frac{\delta V}{\delta z}+w\frac{\delta^{2}V}{\delta z\delta x}-\frac{\delta f}{\delta x}v-f\frac{\delta v}{\delta x}}$

右边可得：

$-\frac{1}{\rho}\frac{\delta P}{\delta y}+Fy \Rightarrow -\frac{\delta(\frac{1}{\rho })}{\delta x}\frac{\delta p}{\delta y}-\frac{1}{\rho }\frac{\delta^{2}}{\delta y \delta x}+\frac{\delta Fy}{\delta x}\Rightarrow\frac{1}{\rho ^{2}}\frac{\delta \rho }{\delta x}\frac{\delta p}{\delta y}-\frac{1}{\rho }\frac{\delta^{2}}{\delta y\delta x}+\frac{\delta Fy}{\delta x}$

可得(4)：

$\large{\frac{\delta^{2} V}{\delta t\delta x}+\frac{\delta u}{\delta x}\frac{\delta V}{\delta x}+u\frac{\delta^{2} V}{\delta x^{2}}+\frac{\delta V}{\delta x} \frac{\delta V}{\delta y}+v\frac{\delta^{2} V}{\delta y\delta x}+\frac{\delta w}{\delta x}\frac{\delta V}{\delta z}+w\frac{\delta^{2}V}{\delta z\delta x}+\frac{\delta f}{\delta x}v+f\frac{\delta v}{\delta x}=\frac{1}{\rho ^{2}}\frac{\delta \rho }{\delta x}\frac{\delta p}{\delta y}-\frac{1}{\rho }\frac{\delta^{2}}{\delta y \delta x}+\frac{\delta Fy}{\delta x}}$

用(4)-(3)，左边：

$\large{\color{red}{\frac{\delta^{2} V}{\delta t\delta x}+\frac{\delta u}{\delta x}\frac{\delta V}{\delta x}+u\frac{\delta^{2} V}{\delta x^{2}}+\frac{\delta V}{\delta x} \frac{\delta V}{\delta y}+v\frac{\delta^{2} V}{\delta y\delta x}+\frac{\delta w}{\delta x}\frac{\delta V}{\delta z}+w\frac{\delta^{2}V}{\delta z\delta x}-\frac{\delta f}{\delta x}v-f\frac{\delta v}{\delta x}}-\color{green}{(\frac{\delta^{2} u}{\delta t\delta y}+\frac{\delta u}{\delta x}\frac{\delta u}{\delta y}+u\frac{\delta^{2} u}{\delta x\delta y}+\frac{\delta v}{\delta t} \frac{\delta u}{\delta y}+v\frac{\delta^{2} u}{\delta y^{2}}+\frac{\delta w}{\delta y}\frac{\delta u}{\delta z}+w\frac{\delta^{2}u}{\delta z\delta y}-\frac{\delta f}{\delta y}v-f\frac{\delta v}{\delta y})}}$

从而可得

$\large{(\frac{\delta^{2} V}{\delta t\delta x}-\frac{\delta^{2} u}{\delta t\delta y})+(\frac{\delta u}{\delta x}\frac{\delta V}{\delta x}-\frac{\delta u}{\delta x}\frac{\delta u}{\delta y})+(u\frac{\delta^{2} V}{\delta x^{2}}-u\frac{\delta^{2} u}{\delta x\delta y})+(\frac{\delta V}{\delta x} \frac{\delta V}{\delta y}-\frac{\delta v}{\delta t} \frac{\delta u}{\delta y})+(v\frac{\delta^{2} V}{\delta y\delta x}-v\frac{\delta^{2} u}{\delta y^{2}})+(\frac{\delta w}{\delta x}\frac{\delta V}{\delta z}-\frac{\delta w}{\delta y}\frac{\delta u}{\delta z})+(w\frac{\delta^{2}V}{\delta z\delta x}-w\frac{\delta^{2}u}{\delta z\delta y})+\frac{\delta f}{\delta x}v+f\frac{\delta v}{\delta x}+\frac{\delta f}{\delta y}v+f\frac{\delta v}{\delta y}}$

$\Rightarrow$

$\large{\color{red}{\frac{\delta}{\delta t}}(\frac{\delta^{} V}{\delta x}-\frac{\delta^{} u}{\delta y})+\color{red}{\frac{\delta u }{\delta x}}(\frac{\delta V}{\delta x}-\frac{\delta u}{\delta y})+\color{red}{u\frac{\delta}{\delta x}}(\frac{\delta^{} V}{\delta x}-\frac{\delta^{} u}{\delta y})+\color{red}{{ V}}(\frac{\delta V}{\delta x}-\frac{\delta u}{\delta y})\color{red}{\frac{\delta }{\delta y}}+\color{red}{v\frac{\delta}{\delta y} }(\frac{\delta^{} V}{\delta x}-\frac{\delta^{} u}{\delta y})+\color{red}{\delta w}(\frac{\delta V}{\delta x}-\frac{\delta u}{\delta y})\color{red}{\frac{1}{\delta z}}+\color{red}{w\frac{\delta}{\delta z}}(\frac{\delta^{}V}{\delta x}-\frac{\delta^{}u}{\delta y})+\frac{\delta f}{\delta x}v+f\frac{\delta v}{\delta x}+\frac{\delta f}{\delta y}v+f\frac{\delta v}{\delta y}}$

右边：

$\large{\color{red}{\frac{1}{\rho ^{2}}\frac{\delta \rho }{\delta x}\frac{\delta p}{\delta y}-\frac{1}{\rho }\frac{\delta^{2}}{\delta y \delta x}+\frac{\delta Fy}{\delta x}}-\color{green}{\frac{1}{\rho ^{2}}\frac{\delta \rho }{\delta y}\frac{\delta p}{\delta x}-\frac{1}{\rho }\frac{\delta^{2}}{\delta x \delta y}+\frac{\delta Fx}{\delta y}}}$

$\Rightarrow$

$\large{\frac{1}{\rho ^{2}}\frac{\delta \rho }{\delta x}\frac{\delta p}{\delta y}-\frac{1}{\rho ^{2}}\frac{\delta \rho }{\delta y}\frac{\delta p}{\delta x}-\frac{1}{\rho }\frac{\delta^{2}}{\delta x \delta y}-\frac{1}{\rho }\frac{\delta^{2}}{\delta y \delta x}+\frac{\delta Fy}{\delta x}+\frac{\delta Fx}{\delta y}}$

令 $\zeta=\frac{\delta V}{\delta x}-\frac{\delta u}{\delta y}$

左边： $\large{\color{red}{\frac{\delta}{\delta t}}(\zeta)+\color{red}{\frac{\delta u }{\delta x}}(\zeta)+\color{red}{u\frac{\delta}{\delta x}}(\zeta)+\color{red}{{\frac{\delta V}{\delta y}}}(\zeta)+\color{red}{v\frac{\delta}{\delta y} }(\zeta)+\color{red}{\frac{\delta w}{\delta z}}(\zeta)+\color{red}{w\frac{\delta}{\delta z}}(\zeta)+\frac{\delta f}{\delta x}v+f\frac{\delta v}{\delta x}+\frac{\delta f}{\delta y}v+f\frac{\delta v}{\delta y}}$

右边：

$\large{\frac{1}{\rho ^{2}}\frac{\delta \rho }{\delta x}\frac{\delta p}{\delta y}-\frac{1}{\rho ^{2}}\frac{\delta \rho }{\delta y}\frac{\delta p}{\delta x}+\frac{\delta Fy}{\delta x}+\frac{\delta Fx}{\delta y}}$

进而：

$\large{\color{red}{\frac{\delta}{\delta t}}(\zeta)+(\vec{V}.\bigtriangledown )\zeta+\color{red}{\frac{\delta u }{\delta x}}(\zeta)+\color{red}{{\frac{\delta V}{\delta y}}}(\zeta)+\color{red}{\frac{\delta w}{\delta z}}(\zeta)+\frac{\delta f}{\delta x}v+f\frac{\delta v}{\delta x}+\frac{\delta f}{\delta y}v+f\frac{\delta v}{\delta y}=\frac{1}{\rho ^{2}}\frac{\delta \rho }{\delta x}\frac{\delta p}{\delta y}-\frac{1}{\rho ^{2}}\frac{\delta \rho }{\delta y}\frac{\delta p}{\delta x}+\frac{\delta Fy}{\delta x}+\frac{\delta Fx}{\delta y}}$