L51.【LeetCode题解】LCR 072. x 的平方根 (6种方法)-CSDN博客

https://leetcode.cn/problems/jJ0w9p/description/

给定一个非负整数 x ，计算并返回 x 的平方根，即实现 int sqrt(int x) 函数。

正数的平方根有两个，只输出其中的正数平方根。

如果平方根不是整数，输出只保留整数的部分，小数部分将被舍去。

示例 1：
输入: x = 4
输出: 2
示例 2：
输入: x = 8
输出: 2
解释: 8 的平方根是 2.82842...，由于小数部分将被舍去，所以返回 2
提示：

0 <= x <= 2^31 - 1

注意：本题与主站 69 题相同： 69. x 的平方根 - 力扣（LeetCode）

2.分析

方法1:调用库函数sqrt

class Solution {
public:
    int mySqrt(int x) 
    {
        return (int)sqrt(x);
    }
};

这种方法没有达到训练的效果

提交结果:

方法2:借用"外挂":改进版卡马克逆平方根算法

原版卡马克逆平方根算法代码

计算 $\frac{1}{\sqrt x}$ ,来自Quake III的源代码:

float Q_rsqrt(float number)
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;
	x2 = number * 0.5F;
	y = number;
	i = *(long*)&y; // evil floating point bit level hacking
	i = 0x5f3759df - (i >> 1); // what the fuck?
	y = *(float*)&i;
	y = y * (threehalfs - (x2 * y * y)); // 1st iteration
 //y = y * (threehalfs - (x2 * y * y)); // 2nd iteration, this can be removed
    return y;
}

方法的可行性验证

其中最有趣的地方在i = 0x5f3759df - (i >> 1);

其中0x5f3759df称为卡马克常数,1st iteration为第一次迭代(牛顿迭代法)

测试代码的计算结果

接入main函数测试,设number == 2

int main()
{
	float number = 2.0;
	float ret = floatQ_rsqrt(number);
	printf("%.30f", ret);
}

备注:threehalfs变量为three+half==3/2

对比C自带的math库下的sqrt(x)

float类型下

#include <stdio.h>
#include <math.h>
int main()
{
	float a = 1.0 / sqrt(2);
	printf("%.30f", a);
}

double类型下

#include <stdio.h>
#include <math.h>
int main()
{
	double a = 1.0 / sqrt(2);
	printf("%.60f", a);
}

再对比win11计算器的结果

取1.0/sqrt(2)的double类型的值的小数点后23位0.70710678118654746171500,与卡马克常数计算的结果0.70693004131317138671875进行误差分析

0.70710678118654746171500-0.70693004131317138671875 = 0.00017673987337607499625

误差:

$\delta =0.00017673987337607499625/0.70710678118654746171500=2.4994792594054877986647651894286*10^{-4}$

$\delta \approx 0.025\%$ 误差极小

代码

版本1(精度低,最多只能通过99.8%的用例)

如果直接使用原版的代码,LeetCode会报错:

class Solution {
public:
    float Q_rsqrt(float number)
    {
        long i;
        float x2, y;
        const float threehalfs = 1.5F;
        x2 = number * 0.5F;
        y = number;
        i = *(long*)&y;
        i = 0x5f3759df - (i >> 1); 
        y = *(float*)&i;
        y = y * (threehalfs - (x2 * y * y));
        return y;
    }
    int mySqrt(int x) 
    {
        return (int)(1/Q_rsqrt((float)x));
    }
};

问题出在: i = *(long*)&y;和y = *(float*)&i;

y是float类型,将y的指针强制类型转换为long,之后解引用给i,即将float在内存中4个字节以long的形式存储,但long是8个字节,因此会报"insufficient space"

可以这样改:i = *(int*)&y;将int转化为long是可以的,或者使用memcpy直接拷贝内存:

memcpy(&i, &y, sizeof(int));
memcpy(&y, &i, sizeof(int));

提交后仍然会有问题:精度低

可以多次迭代提高精度:

两次迭代:

三次迭代:

四次迭代:

......

十次迭代:

可见,虽然迭代次数变多了,但是精度没有提高,归根结底在于float的精度比较低,可以改成double试试

版本2(用例全部通过)

为double,需要使用double类型下的快速平方根的魔数0x5fe6ec85e4c34e2d

class Solution {
public:
    double Q_rsqrt(double number)
    {
        long long i;
        double x2, y;
        const double threehalfs = 1.5;
        x2 = number * 0.5;
        y = number;
        memcpy(&i, &y, sizeof(double));
        //0x5fe6ec85e4c34e2d为double类型的魔数
        i = 0x5fe6ec85e4c34e2d - (i >> 1); 
        memcpy(&y, &i, sizeof(double));
        y = y * (threehalfs - (x2 * y * y)); 
        y = y * (threehalfs - (x2 * y * y)); 
        y = y * (threehalfs - (x2 * y * y));
        return y;
    }
    int mySqrt(int x) 
    {
        double tmp=1/Q_rsqrt((double)x);
        int ret=(int)tmp;
        return ret;
    }
};

(经过验证,只需要三次迭代就能通过所有的用例)

提交结果:

方法3:牛顿迭代法

原理

求 $\sqrt{x}$ ,设 $x^2=C$ ,那么可以求 $y=x^2-C$ 的零点

以求 $\sqrt{2}$ 的近似值为例:

找曲线上一点作切线即可:

再作切线迭代:

则可写出迭代方程:

$x_i=\frac{1}{2}\cdot x_{i-1} +\frac{C}{2\cdot x_{i-1}}$

备注:卡马克常数就是这么推的

方法1:迭代固定次数

class Solution {
public:
    int mySqrt(int x) 
    {
        if (x==0)
           return 0;
        int c=x;
        double tmp=x;
        int t=20;
        while(t--)
        tmp=0.5*tmp+0.5*c/tmp*1.0;
        return (int)tmp;

    }
};

经尝试,迭代20次刚好能通过全部的测试用例

提交结果:

方法2:到达满足精度要求退出循环

设精度为1e-1,若tmp*tmp-c的差值小于1e-1就退出循环

class Solution {
public:
    int mySqrt(int x) 
    {
        if (x==0)
           return 0;
        double tmp=x,c=x;
        while(fabs(tmp*tmp-c)>1e-1)
        {
            tmp=0.5*tmp+0.5*c/tmp*1.0;
        }        
        return (int)tmp;
    }
};

提交结果:

方法4:循环枚举

由于题目说了"如果平方根不是整数，输出只保留整数的部分，小数部分将被舍去",那就可以一个一个枚举所有整数

class Solution {
public:
    int mySqrt(int x) 
    {
        for (long long i=0;i<=x;i++)
        {
            if (i*i<=x&&(i+1)*(i+1)>x)
                return i;
        }
        return -1;
    }
};

注意这里i的类型要选long long,因为i*i可能会超过int

提交结果:

方法5:内联汇编

前置知识

为了尽量提高精度,使用sqrtsd开方指令,以下是Intel开发手册中第1890页的介绍

读资料可知:sqrtsd只支持浮点数寄存器,因此需要将参数x转化为浮点数

按照x86_64 ABI的接口规则,函数的第一个参数存入rdi寄存器中,需要将rdi的值转化为双精度浮点数,使用cvtsi2sd指令,以下是Intel开发手册中第894页的介绍:

注意指令对操作大小的要求,为有符号整型,对应C语言的int,4字节,应该使用rdi的低32位edi

cvtsi2sd xmm0,edi

按照sqrtsd对寄存器的要求,

之后对xmm0寄存器的值开方,结果存入xmm0寄存器中

sqrtsd xmm0,xmm0

将xmm0寄存器的值转化为int类型后返回,可以使用cvttsd2si指令,以下是Intel开发手册中第912页的介绍:

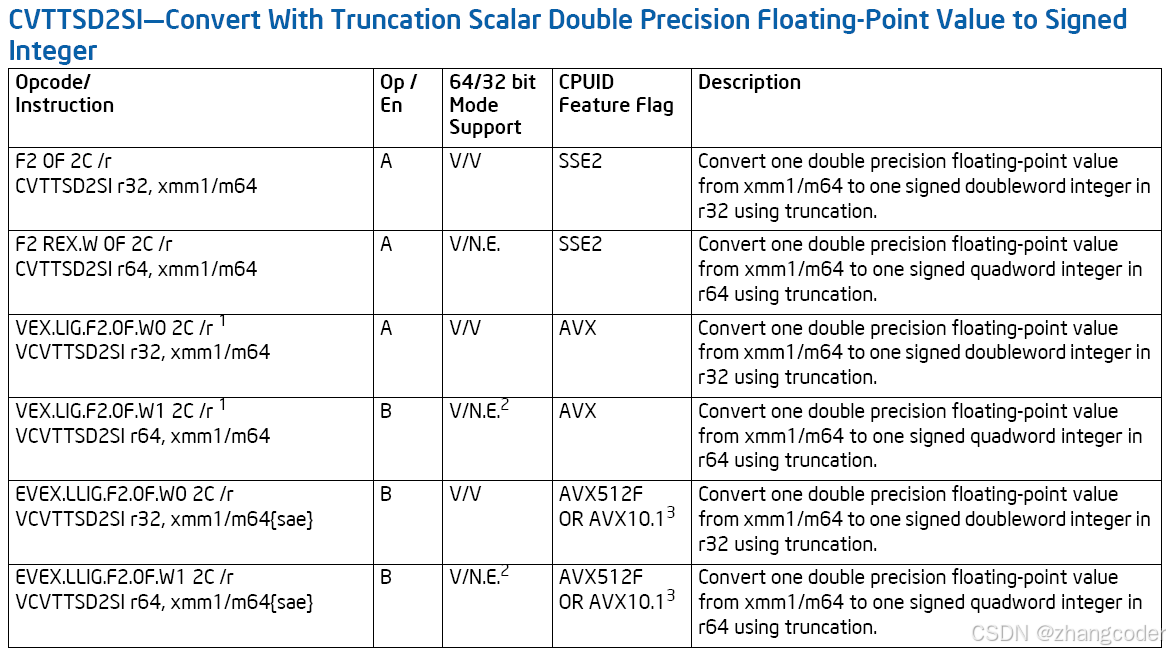
按照cvttsd2si对寄存器的要求,

源操作数使用xmm寄存器,目的操作数使用通用寄存器eax,且eax是X86_64 ABi规则中返回函数处理结果的rax寄存器低32位

代码

__attribute__((naked))
int mySqrt(int x)
{
    __asm__ volatile
    (
        ".intel_syntax noprefix;"
        "cvtsi2sd xmm0,edi;"
        "sqrtsd xmm0,xmm0;"
        "cvttsd2si eax,xmm0;"
        ".att_syntax;"
        "ret;"                        
    );
}

提交结果: