
图1-链表的结构示意图
上图所示的节点细节如下:
- 首个结点中next1存放的是第二结点的内存地址,因此用一个箭头指向第二个结点,就可以表示两个结点之间的关系。
- 最后一个结点的后面不再有其他结点,因此最后结点的next5指针域中没有地址内容,编程中可以用null表示。
3. 特点
通过上文所述,就可以给大家总结出链表的主要特点:
(1). 从内存结构来看,链表的内存结构是不连续的内存空间,是将一组零散的内存块串联起来,从而进行数据存储的数据结构;
(2). 链表由一系列结点组成,每个结点包括两个部分,一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。链表中数据元素的逻辑顺序就是通过地址指针实现的;
(3). 链表和数组相比,内存空间消耗更大,因为每个存储数据的结点都需要额外的空间存储地址指针。
二. 链表分类
在工作实践中,开发者接触到的链表主要有三种:单向链表、双向链表、循环链表。下面给大家逐一进行介绍一下。
1. 单向链表
单向链表的每一个结点包含两部分,一部分是存放数据的变量data,另一部分是指向下一个结点的指针next。 单链表只能单向读取,其结构如下所示:

图2-单向链表结构示意图
们以Java为例,给出单向链表的结构定义:
class Node{
Object value;
Node next;
}
2. 双向链表
双向链表,表示链表结点由三部分组成:数据域、下一结点指针域、前一结点指针域。
在双向链表结构中,既可以从首个结点出发,根据下一结点指针域依次找到所有结点;同理,也可以从指定的某个结点,根据结点中的前一结点指针地址,向前依次得到前面的结点。具体地,双向链表的结构示意图如下所示:

图3-双向链表结构示意图
如上图所示:
- 第1个结点作为整个链表的首结点,该结点的prev1指针内容为null,表示没有前一个结点。
- 第5个结点作为整个链表的最后结点,next5指针内容为null,表示后续没有下一个结点。
- 除此之外,中间三个结点,next指针和prev指针分别指向下一个结点和前一个结点,可以实现双向查找。
使用Java进行双向链表的结点结构定义如下:
class Node{
Object value;
Node next;
Node prev;
}
3. 循环链表
如果,我们将链表的最后结点的next指针域做下修改,由原来的指向null修改为指向第1个结点,则整个链表就变成了一个环路。以单向链表进行操作,如下图所示:

图4-单向循环链表示意图
如上图,每个结点有数据域和指针域两个部分,这种循环链表被称之为单向循环链表。在计算机领域中,单向循环链表又称约瑟夫环(Josephu Loop),这一点仅做了解即可。当然,双向链表也可以调整为循环的链表,被称之为双向循环链表,如下图所示:

图5-双向循环链表示意图
三. 存储原理
数组在内存中的存储方式是顺序存储(连续存储),链表在内存中的存储方式则是随机存储,如下图所示:

图6-链表的内存存储示意图
链表的每一个结点分布在内存的不同位置,依靠next指针关联起来。这样可以灵活有效地利用零散的碎片空间。链表的第一个结点被称为头结点,没有任何结点的next指针指向它,它的前置结点为空null。头结点用来记录链表的基地址。有了它,就可以遍历得到整条链表的数据。链表的最后一个结点被称为尾结点,它的next指向为空null。
四. 链表常见操作
本篇文章内容,我们以单向链表为例,介绍链表的常见操作,主要包括:查找结点、更新结点、插入结点和删除结点等操作。
1. 查找结点
在查找元素时,链表只能从头结点开始向后,一个结点一个结点逐一查找,如下图所示:

图7-单向链表查找结点示意图
时间复杂度分析,分两种情况:
- 查找头结点:头结点是链表的第一个结点,直接就能得到结果,因此查找头结点时间复杂度是O(1)。
- 查找非头结点:如果查找非头结点,则需要从头结点向后依次查找,知道整个链表的末尾,因此查找非头结点的其他结点时,时间复杂度是O(n),最坏情况下时间复杂度也是O(n)。
2. 更新结点
更新结点操作需要两个步骤:
- 找到要更新的结点;
- 将旧数据替换成新数据。
如下图所示:
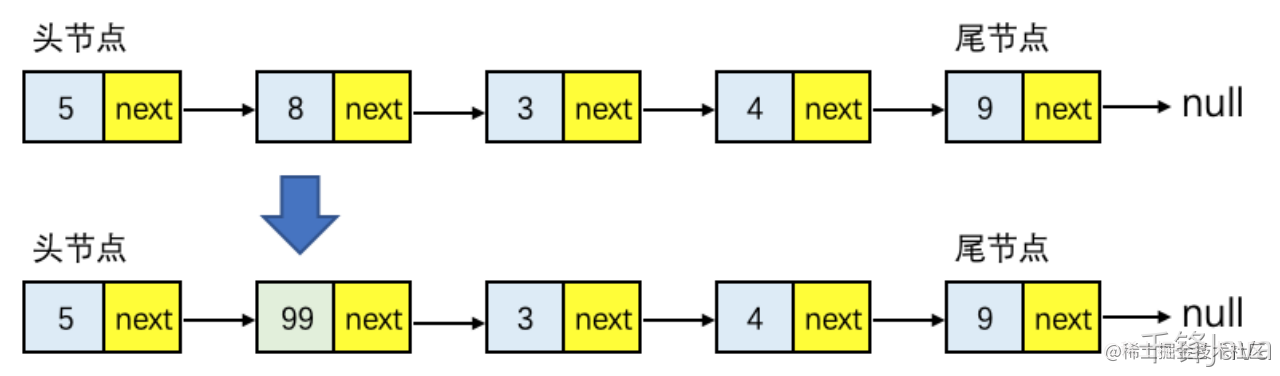
图8-单向链表更新结点数据操作示意图
与查找结点操作时间复杂度情况类似,更新时间复杂度分两种情况:
- 更新头结点:单向链表更新头结点的时间复杂度是O(1);
- 更新非头结点:更新其他结点的最坏情况时间复杂度是O(n)。
3. 插入结点
3.1 尾部插入
尾部插入即把最后一个结点的next指针指向新插入的结点即可,如下图所示:
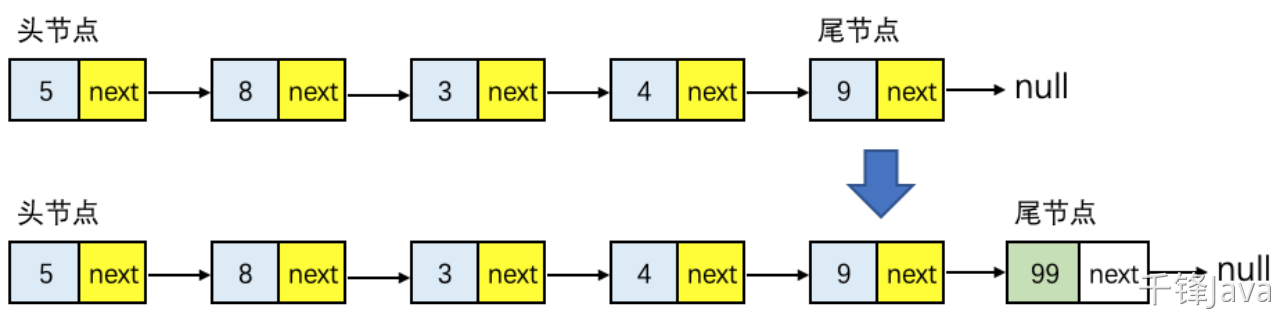
图9-单向链表尾部插入结点示意图
时间复杂度分析:如上图所示,若尾部插入结点,则需要从头开始遍历,因此单向链表添加尾结点的时间复杂度是O(n)。
3.2 头部插入
头部插入新结点需要两个步骤:
(1). 把新结点的next指针指向原先的头结点;
(2). 把新结点变为链表的头结点。
如下图所示:
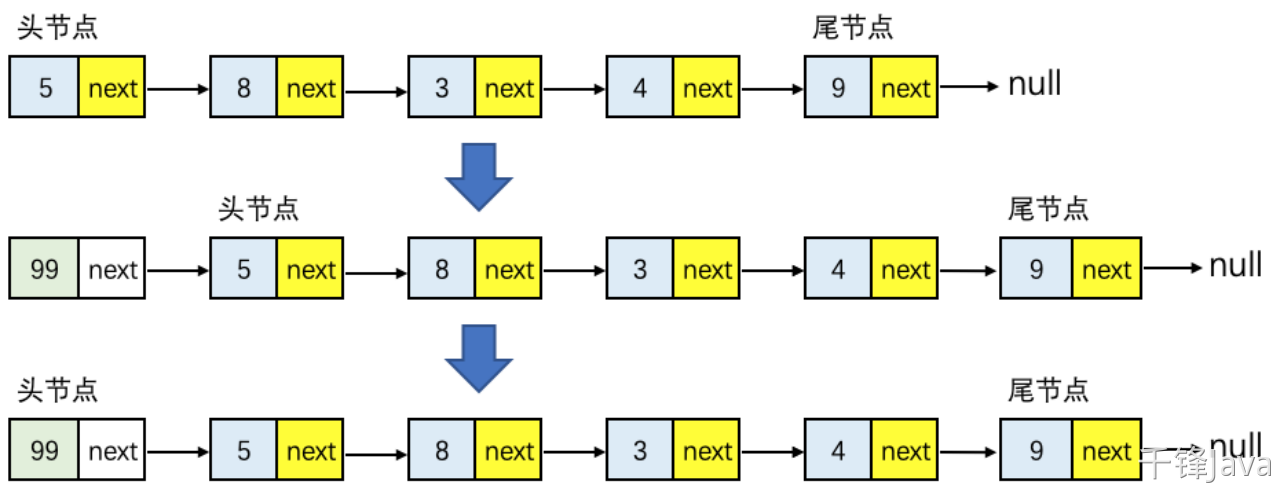
图10-单链表头部插入结点示意图
时间复杂度分析:因为直接将新节点的指针域指向头结点即可完成操作,因此添加头结点的时间复杂度是O(1)。
3.3 中间插入
在链表的中间位置插入结点同样需要三步:
(1). 从头结点开始向后查找,找到要插入的结点的位置;
(2). 新结点的next指针指向插入位置的结点;
(3). 插入位置前置结点的next指针指向新结点;
示意图如下:
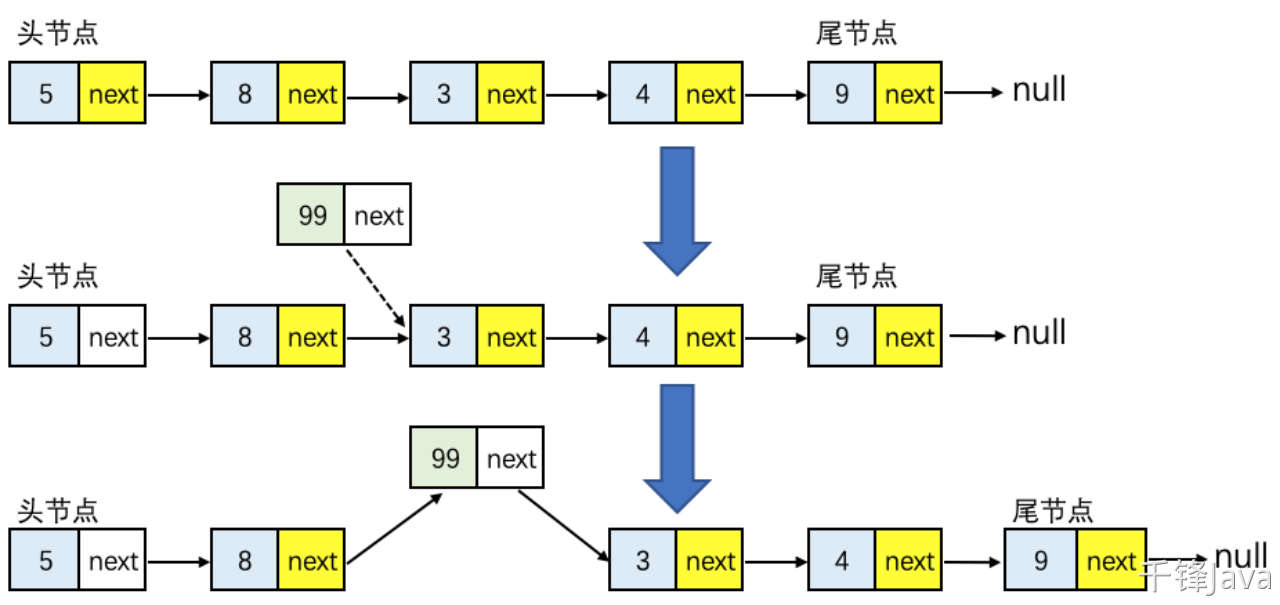
图11-单向链表中间位置插入结点
时间复杂度分析: 若执行插入结点操作,首先需要从头结点向后查找,找到要插入的位置。很明显,与链表的规模有关,因此中间插入结点操作的时间复杂度是O(n)。
4. 删除结点
4.1 尾部删除
若希望删除链表的最后一个结点,只需要将倒数第二个结点的指针域指向null即可,如下图所示:
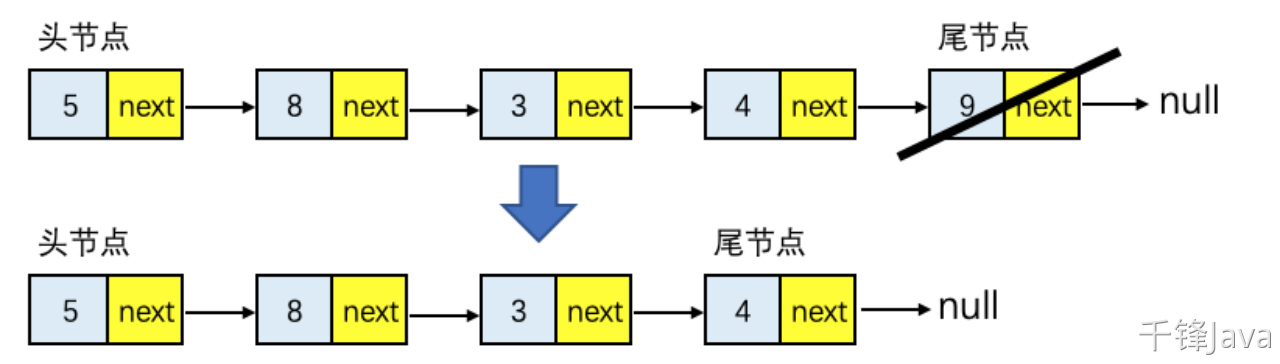
图12-单向链表尾部删除结点示意图
时间复杂度分析: 因为要从头开始遍历,所以单向链表删除尾结点的时间复杂度是O(n)。
4.2 头部删除
头部删除与头部插入操作类似,只需要把链表的头结点设为原先头结点的next指针即可如图:
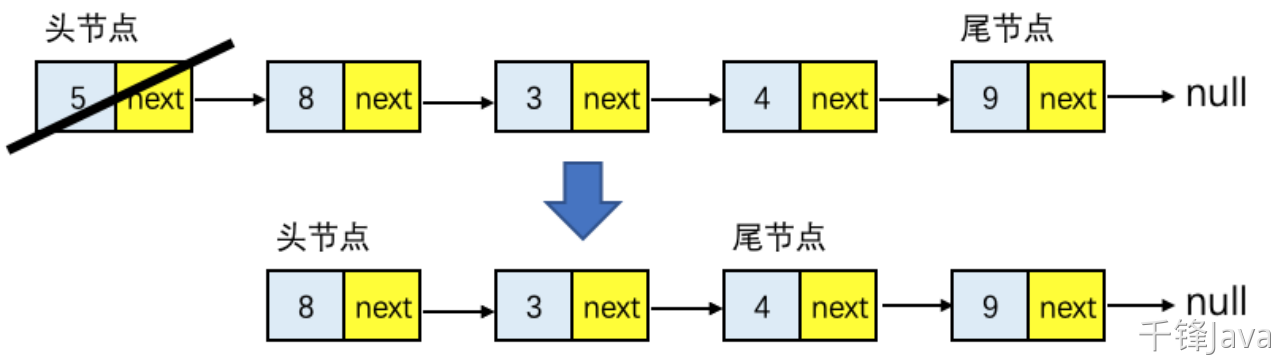
图13-单向链表头部删除结点示意图
时间复杂度分析: 删除头结点的时间复杂度也是O(1)。
4.3 中间删除
中间位置删除结点操作类似于中间插入操作,需要三步:
5376796325)]
图12-单向链表尾部删除结点示意图
时间复杂度分析: 因为要从头开始遍历,所以单向链表删除尾结点的时间复杂度是O(n)。
4.2 头部删除
头部删除与头部插入操作类似,只需要把链表的头结点设为原先头结点的next指针即可如图:
[外链图片转存中…(img-ya6VRtjz-1725376796325)]
图13-单向链表头部删除结点示意图
时间复杂度分析: 删除头结点的时间复杂度也是O(1)。
4.3 中间删除
中间位置删除结点操作类似于中间插入操作,需要三步:





















 895
895

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








