描述:
归并排序是利用归并的思想实现的排序方法,该算法采用经典的分治策略即将问题分成一些小的问题然后递归求解,而治的阶段则将分的阶段得到的各答案 “修补” 在一起,即分而治之 。
归并排序是稳定排序,它也是一种十分高效的排序,能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了 名为TimSort的排序算法,就是归并排序的优化版本。每次合并操作的平均时月复杂度为O(n),而完全二叉树的深度为|1og2n|。总的平均时间复杂度为O(nlogn)。而旦,归并排序的最好,最坏,平均时间复杂度均为o(nlogn)。
归井排序核心思想是先分再治,具体算法描述如下:
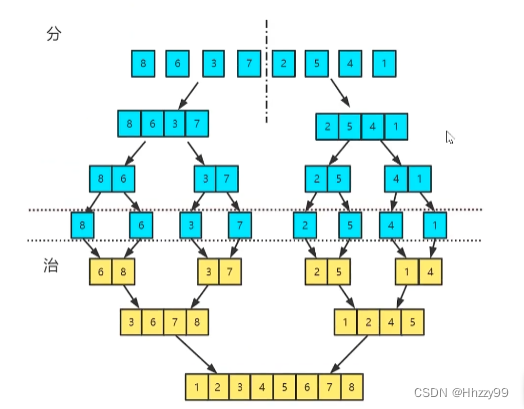
先将未排序数组/2进行分组,然后再将分好组的数组继续/2再次分组,直到无法分组,这个就是分的过程。
然后再将之后把两个数组大小为1的合并成一个大小为2的,再把两个大小为2的合并成4的,同时在合并的过程中完成数组的排列,最终直到全部小的数组合并起来,这个就是治的过程。
实现
分解1: 先实现分的思想,将数组分解进行实现
先获取数组的中轴,然后以中轴将数组分为两个部分
使用递归分别执行左右两部分分解
public static void main(String[] args) {
int[] arrs = {8,6,3,7,2,5,4,1};
mergeSort(arrs,0,arrs.length-1);
}
//实现归并排序
public static void mergeSort(int[] arrs, int first, int last){
//实现递归推出的条件
if(first >= last){
return;
}
//求出当前数组的中间值
int mid = (first + last)/2;
//将左边的数组继续分解
mergeSort(arrs,first,mid);
//将右边的数组继续分解
mergeSort(arrs,mid + 1, last);
//输出分组情况
//先输出左边的数组
for (int i = first; i <= mid; i++){
System.out.print(arrs[i] + " ");
}
System.out.print("--------");
//输出右边的数组
for (int i = mid + 1; i <= last; i++) {
System.out.print(arrs[i] + " ");
}
System.out.println(" ");
}
分解2: 实现具体治的过程,将左右两个数组合并到一个临时数组中
分别设计两指针i和j,遍历左右两个数组,取出元素进行比较,将小的元素放入到临时数组中。
然后将左右剩下的元素放入到数组中
将排序好的临时数组中的元素返回到未排序的数组中
public static void main(String[] args) {
int[] arrs = {8,6,3,7,2,5,4,1};
mergeSort(arrs,0,arrs.length-1);
//输出排序结果
for (int i = 0; i < arrs.length; i++) {
System.out.print(arrs[i] + " ");
}
}
//实现归并排序
public static void mergeSort(int[] arrs, int first, int last) {
//实现递归推出的条件
if (first >= last) {
return;
}
//求出当前数组的中间值
int mid = (first + last)>>>1;
//将左边的数组继续分解
mergeSort(arrs, first, mid);
//将右边的数组继续分解
mergeSort(arrs, mid + 1, last);
//治,实现插入并完成排序
int[] temp = new int[last + 1];
//定义两个指针
int i = first;//左边数组的遍历指针
int j = mid + 1;//右边数组的遍历指针
int t = 0;//临时数组的指针
//遍历左右两个数组,将较小的元素插入到临时数组中
while (i <= mid && j <= last) {
if (arrs[i] <= arrs[j]) {
//将左边的指针指向的元素插入到临时数组中
temp[t++] = arrs[i++];
} else {
//将右边的指针指向的元素插入到临时数组中
temp[t++] = arrs[j++];
}
}
//再将左右剩余的元素插入到临时数组中
while (i<=mid){
temp[t++] = arrs[i++];
}
while (j<=last){
temp[t++] = arrs[j++];
}
//还需要将临时数组中的元素复制到原始数组中
//先将t重置
t = 0;
//将t指向的值,复制到first指向的原始数组的位置
while (first <= last){
arrs[first++] = temp[t++];
}
}
3.快速排序
描述:
快速排序是对冒泡排序的一种改进,通过分而治之的思想减少排序中交换和遍历的次数,整个过程可以通过递归的方式完成。
具体描述如下:
1.首先通过比较算法,找到基准数,比较过程通过交换最终达到基准数左边的数字都比右边的小。
2.然后以基准数作为中轴,将数组分为两部分,分别执行步骤1的算法(可以通过递归实现),直到无法再次分割排序完毕
递归
一个含直接或间接调用本函数语句的函数被称之为递归函数,他必须满足以下两个条件:
1)在每一次调用自己时,必须是(在某种意义上)更接近于解;
2)必须有一个终止处理或计算的准则;
基本格式
void func()
{
//递归条件
if(condition)
func();
else
//退出递归
}
实现
分解1: 创建左右两个指针,将最后一个值作为基准值,通过不断交换将数组分为两部分,左边的比右边的要小。
- 先判断左指针和基准的值,如果小于等于就向后移动,直到遇到比基准值大的值
- 再判断右边指针和基准值,如果大于等于就向前移动,直到遇到比基准值小的值
- 然后交换左右指针的值
- 循环上述操作,直到左右指针重合,然后交换重合值和基准值
public static void main(String[] args) {
int[] arrs = {3,9,8,7,2,5,4,1,6};
//执行快速排序
quickSort(arrs);
for (int i = 0; i < arrs.length; i++) {
System.out.print(arrs[i] + " ");
}
}
//定义快速排序方法
public static void quickSort(int[] arrs){
//定义左指针
int left = 0;
//定义右指针
int right = arrs.length - 1;
//定义基准值
int pos = arrs.length - 1;
while (left != right){
//判断左指针是否比基准值大,如果大就停止移动
while(arrs[left] <= arrs[pos]){
left++;
}
if(left == right)
break;
//判断右指针是否比基准值小,如果小就停止移动
while (arrs[right] >= arrs[pos]){
right--;
}
if(left < right){
//交换左右指针指向的值
int temp = arrs[left];
arrs[left] = arrs[right];
arrs[right] = temp;
}
}
//当left和right重合之后,需要将重合的值和基准值进行交换
int temp = arrs[left];
arrs[left] = arrs[pos];
arrs[pos] = arrs[left];
}
分解2: 将以left和right的重复位置作为中轴,将数组分为两部分,左右分别执行分解1的操作,直到排序完成
public static void main(String[] args) {
int[] arrs = {3,9,8,7,2,5,4,1,6};
//执行快速排序
quickSort(arrs, 0, arrs.length-1);
for (int i = 0; i < arrs.length; i++) {
System.out.print(arrs[i] + " ");
}
}
//定义快速排序方法
public static void quickSort(int[] arrs, int first, int last){
//设置一下递归退出条件
if(first >= last)
return;
//定义左指针
int left = first;
//定义右指针
int right = last;
//定义基准值
int pos = last;
//当left不等于right
while (left != right){
//判断左指针是否比基准值大,如果大就停止移动
while(arrs[left] <= arrs[pos]){
left++;
}
//判断右指针是否比基准值小,如果小就停止移动
while (arrs[right] >= arrs[pos] && left < right){
right--;
}
if(left < right){
//交换左右指针指向的值
int temp = arrs[left];
arrs[left] = arrs[right];
arrs[right] = temp;
}
}
//当left和right重合之后,需要将重合的值和基准值进行交换
int temp = arrs[left];
arrs[left] = arrs[pos];
arrs[pos] = temp;
//将左边的数组执行快速排序
quickSort(arrs, first,left - 1);
//将右边的数组执行快速排序
quickSort(arrs,right + 1,last);
}
4.计数排序
描述:
计数排序是一个非基于比较的排序算法,该算法于1954年由Harold H.Seward,提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为o(n+k)(其中k是整数的范围),快于任何比较排序算法。当然这是一种牺牲空间换取时间的做法,而且当O(k)>O(nlog(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(nlog(n)),如归并排序,堆排序)
计数排序是一种适合于最大值和最小值的差值不是不是很大的排序,也就是说重复的数据会比较多的情况。
实现
分解1: 找到最大的数字,并且以数字的大小创建一个统计数组
//分解1:根据最大值创建统一数组
//遍历数组找到最大的值
int max = arrs[0];
for (int i = 0; i < arrs.length; i++) {
if(arrs[i] > max){
max = arrs[i];
}
}
//根据最大值创建统一数组
int[] countArrs = new int[max];
分解2: 遍历未排序的数组,统计每个数字出现的次数,根据下标添加到新的统计数组中
for (int i = 0; i < arrs.length; i++) {
//以arrs[i]作为下标++
countArrs[arrs[i]]++;
}
分解3: 将排序的结果返回到原先的数组中
public static void main(String[] args) {
int[] arrs = {0,2,1,3,0,2,0,1,1};
//分解1:根据最大值创建统一数组
//遍历数组找到最大的值
int max = arrs[0];
for (int i = 0; i < arrs.length; i++) {
if(arrs[i] > max){
max = arrs[i];
}
}
//分解2:
//根据最大值创建统一数组
int[] countArrs = new int[max + 1];//注意考虑0,要加一个
//遍历原先数组
for (int i = 0; i < arrs.length; i++) {
//以arrs[i]作为下标++
countArrs[arrs[i]]++;
}
//分解3:将统计数组对应的下标的数字返回到排序数组中
int k = 0;//统计数组的下标
int index = 0;//排序数组的下标
while (k < countArrs.length){
//判断统计数组中的值是否大于0
while(countArrs[k] > 0){
//将对应的下标,返回到排序数组中
arrs[index++] = k;
//统计的数字减少一个
countArrs[k]--;
}
k++;
}
//输出结果
for (int i = 0; i < arrs.length; i++) {
System.out.print(arrs[i] + " ");
}
}
统计数组优化
如果待排序的数字很大,那么在创建数组的时候会浪费没有空间,同时也会导致创建的数组,所以需要进行优化;
可以通过使用最大数字减去最小数字求出需要数组的大小。
public static void main(String[] args) {
int[] arrs = {90,92,91,93,90,92,90,91,91};
//分解1:根据最大值创建统一数组
//遍历数组找到最大和最小的值
int max = arrs[0];
int min = arrs[0];
for (int i = 0; i < arrs.length; i++) {
if(arrs[i] > max){
max = arrs[i];
}
if(arrs[i] < min){
min = arrs[i];
}
}
//分解2:
//根据最大值创建统一数组
int[] countArrs = new int[max - min + 1];//注意考虑0,要加一个
//遍历原先数组
for (int i = 0; i < arrs.length; i++) {


**网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**
x = arrs[i];
}
if(arrs[i] < min){
min = arrs[i];
}
}
//分解2:
//根据最大值创建统一数组
int[] countArrs = new int[max - min + 1];//注意考虑0,要加一个
//遍历原先数组
for (int i = 0; i < arrs.length; i++) {
[外链图片转存中...(img-AKJpekQo-1726122788351)]
[外链图片转存中...(img-7vXZhkGy-1726122788352)]
**网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**





















 1055
1055

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








