考核题解析

力扣82.删除排序链表中的重复元素

82. 删除排序链表中的重复元素 II

给定一个已排序的链表的头 head ， 删除原始链表中所有重复数字的节点，只留下不同的数字 。返回 已排序的链表 。

示例 1：

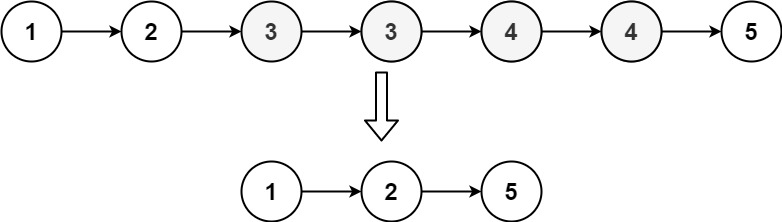
输入：head = [1,2,3,3,4,4,5]
输出：[1,2,5]

示例 2：

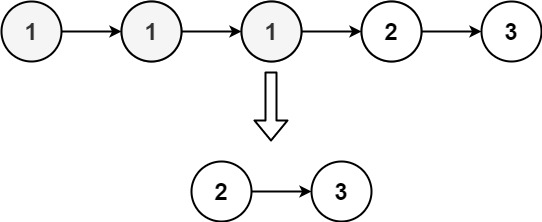
输入：head = [1,1,1,2,3]
输出：[2,3]

提示：

• 链表中节点数目在范围 [0, 300] 内
• -100 <= Node.val <= 100
• 题目数据保证链表已经按升序 排列

题目分析

找到所有重复的元素并在链表中删除。需要用到双指针。

解题思路

这道题不是单纯的删除重复的其中之一个元素，而是要把重复的元素全部删除。我们在遍历链表时需要格外注意这一点。我们的初步思路就是建立虚拟头结点，双指针，首先用pre为cur定位，用cur进行删除操作。因此我们用cur指针遍历链表，每次循环都将cur移动到pre下一个节点的位置。为了找出链表是从什么地方开始重复的，我们使用一个if判断。判断的内容为cur与cur下一节点的值是否相同，并且cur的下一节点不能为空。如果不满足判断条件，直接移动pre到下一节点即可。

如果满足条件，进入if后，我们首先要新建一个node指针来保存cur的位置，因为接下来我们就要移动node，并将node值与cur值进行比较。此时我们使用的是while循环而不是if判断，因为我们无法确定接下来还有多少个节点值是重复的，所以我们不能使用单次判断，而是用while进行多次判断。并且此时我们的判断条件不能是判断node的下一节点是非为空，因为node下一节点是非为空，并不影响我们对于多次重复元素的筛选。反而，如果写成node->next!=NULL,面对{1,2,3,3}这种例子，就会在循环到node指向第二个3时不满足条件而终止循环，从而就会漏删最后一个重复元素。因此我们可以得知，循环条件是非常重要的，多加一个少加一个都会对最后运行结果产生很大的影响。

node的循环结束后，我们让pre直接指向node，就可以把重复值都跳过了。最后返回虚拟头结点ahead的下一节点即可。最后，备注一个点，就是关于虚拟头结点的创建。我们可以像下面展示的一样，先将struct listnode重命名，然后只用写ListNode* ahead=malloc(sizeof(ListNode));即可。如果不进行重命名，就需要写 struct ListNode*ahead=(struct ListNode*)malloc(sizeof(struct ListNode)); ，两种写法需要分清楚。

代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
 struct ListNode* deleteDuplicates(struct ListNode* head) {
    typedef struct ListNode ListNode;
    ListNode* ahead=malloc(sizeof(ListNode)); 
    ahead->next=head;
    struct ListNode* pre=ahead;
    struct ListNode* cur=ahead->next;
    while(cur!=NULL){
        if(cur->next!=NULL&&cur->val==cur->next->val){
            struct ListNode* node=cur;
            while(node!=NULL&&node->val==cur->val){
                node=node->next;
            }
            pre->next=node;
        }
        else{
            pre=pre->next;
        }
        cur=pre->next;
    }
    return ahead->next;
}

力扣19.删除链表的倒数第N个结点

19. 删除链表的倒数第 N 个结点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

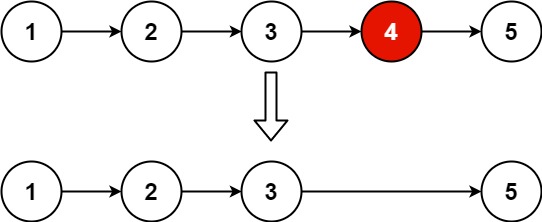
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

输入：head = [1], n = 1
输出：[]

示例 3：

输入：head = [1,2], n = 1
输出：[1]

提示：

• 链表中结点的数目为 sz
• 1 <= sz <= 30
• 0 <= Node.val <= 100
• 1 <= n <= sz

**进阶：**你能尝试使用一趟扫描实现吗？

题目分析

前后双指针遍历链表，后指针删除倒数第N个节点。

解题思路

在这道题中，我们需要找到倒数第N个节点并且删掉它，我们首先就会想到双指针。我们可以总结出来一个规律，凡是链表题里面涉及到找某个节点的，我们都可以使用双指针，这是双指针最基础的考法。我们首先设置一个虚拟头结点，方便我们对前后指针进行操作。我们将前指针指向head，后指针指向虚拟头指针。为什么这一步操作前后指针的起点不一样呢？原因就在于链表删除节点的方式比较特别。我们要删除某个节点，我们必须要知道它前一个节点的地址，移动前一个节点的指针，因此在前后指针移动完毕的时候，后指针其实需要指向倒数第n+1个节点。

那又有一个疑问了，为什么不让前指针多移动一个节点呢？这样前后指针的起点就都会在head处了，不需要再设虚拟头结点了。其实是不可行的，虚拟头结点是一定要设的，前后指针的起点也一定是不一样的。原因就在于对前指针先走几步的移动上。我们这个移动采用的是for循环，因为次数更可控。如果我们的测试用例为{1}，1，如果我们按照上文所说，让前指针多移动一个节点，那就会访问到空节点，就会导致程序报错。因此，为避免以上情况的发生，我们要采用虚拟头结点帮助我们进行后指针的移动。最后输出虚拟头结点的下一个节点即可。

代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* removeNthFromEnd(struct ListNode* head, int n) {
    struct ListNode* dummy = malloc(sizeof(struct ListNode));
    dummy->val = 0;
    dummy->next = head;
    struct ListNode* fast = head;
    struct ListNode* slow = dummy;

    for (int i = 0; i < n; ++i) {
        fast = fast->next;
    }
    while (fast) {
        fast = fast->next;
        slow = slow->next;
    }
    slow->next = slow->next->next;
    return dummy->next;
}

力扣33.搜索旋转排序数组

33. 搜索旋转排序数组

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

提示：

• 1 <= nums.length <= 5000
• -104 <= nums[i] <= 104
• nums 中的每个值都 独一无二
• 题目数据保证 nums 在预先未知的某个下标上进行了旋转
• -104 <= target <= 104

题目分析

升序数列，查找一个target，时间复杂度为 O(log n) ，我们使用二分法解答。

解题思路

这道题与经典二分法不同的地方在于，这个数组将后面部分的元素旋转到前面来了，导致整个数组并不是标准的升序数组。但其实对我们使用二分法的影响不大，我们只需要分清楚target在数组中的位置分几种情况就可以。我们先将二分法的开头打出来（定义left，right，while循环，定义mid），我们这里使用闭区间做法。接下来我们开始分析target在数组中的几种情况：

1. nums[mid]==target：直接返回mid。
2. **数组的left小于mid：**我们首先可以确定mid及其以前的数组肯定是升序的，是旋转得来的，因为未旋转的数组部分都会小于旋转数组的第一个元素。如数组[4,5,6,7,0,1]，此时mid（=2，为6）及其以前的数组元素全是旋转得来的。因此我们可以列出nums[mid]>target&&nums[left]<=target的情况：在这个情况下的target位于升序数组中，正常二分法操作让right=mid-1;即可。如果target不在这个情况内，我们就移动left=mid+1，接下来就会转到第3种的情况中。
3. **数组的left大于mid：**与上一种情况类似的推理，我们可以确定mid及其以后的数组肯定是升序的，是未旋转的部分。如数组[4,5,-2,-1,0,1,2]，此时mid（=3，为-1）及其以后的数组全是未旋转的。因此我们可以列出nums[mid]<target&&nums[right]>=target的情况：在这个情况下的target位于升序数组中，正常二分法操作让left=mid+1;即可。如果target不在这个情况内，我们就移动left=mid+1，接下来就会转到第2种的情况中。

情况分完了，依次用if判断填入循环中即可。while循环结束后，如果没有找到target，就返回-1。

代码实现

int search(int* nums, int numsSize, int target) {
    int left=0,right=numsSize-1;
    while(left<=right){
        int mid=left+((right-left)/2);
        if(nums[mid]==target) return mid;
        if(nums[left]<=nums[mid]){
            if(nums[mid]>target&&nums[left]<=target){
                right=mid-1;
            }
            else left=mid+1;
        }else{
            if(nums[mid]<target&&nums[right]>=target){
                left=mid+1;
            }
            else right=mid-1;
        }
    }
    return -1;
}

力扣LCR 009.乘积小于k的子数组

LCR 009. 乘积小于 K 的子数组

给定一个正整数数组 nums和整数 k ，请找出该数组内乘积小于 k 的连续的子数组的个数。

示例 1：

输入: nums = [10,5,2,6], k = 100
输出: 8
解释: 8 个乘积小于 100 的子数组分别为: [10], [5], [2], [6], [10,5], [5,2], [2,6], [5,2,6]。
需要注意的是 [10,5,2] 并不是乘积小于100的子数组。

示例 2：

输入: nums = [1,2,3], k = 0
输出: 0

提示：

• 1 <= nums.length <= 3 * 104
• 1 <= nums[i] <= 1000
• 0 <= k <= 106

注意：本题与主站 713 题相同：https://leetcode-cn.com/problems/subarray-product-less-than-k/

题目分析

找到连续的一段子数组，要求其中每个元素的乘积小于k。大于和等于都不要。

解题思路

拿到这道题，我们考虑用不定长滑动窗口解决。这个解法有点像双指针，也有点像不定长滑动窗口，所以就不管具体算什么方法了。我们来模拟一下得到答案的过程。我们首先进行初始化，定义左端点left为0，计数ans为0，乘积prod为1。这道题里面，我们使用固定右端点right移动左端点left的方法。设置for循环，枚举right，让prod每次乘上nums[right]，然后进行判断。当prod大于等于k时就要开始移动left，让left++，并让prod除去此时窗口的第一个值，直到窗口内子数组乘积小于k。最后给ans加上right-left+1（后面解释原因）。

这个地方出现了一个疑问，判断prod大于等于k，我们使用if还是while呢？有些人觉得删掉前一个就行了，不需要多次判断啊，示例[10,5,2,6]就不用回退好几步。这个疑问其实很常见，尤其是在这类需要回退的题目里面，我们常常会把本该使用while的判断误写成if，比如用kmp算法求next数组的时候也会遇到这种问题。这就需要具体问题具体分析了。举一个例子：[10,9,10,4,3,8,3,3,6,2,10,10,9,3],k=19，假设此时right=4，left=3，此时[4,3]是符合要求的。接下来枚举移动right。于是right=5了，left没有变化依旧等于3。此时[4,3,8]不符合要求。我们如果使用if，就代表我们只会进行一步回退，只会把[4]踢出窗口，可是剩下的[3,8]也不符合要求，继续这么计算就会导致ans多加了1，导致后面的计算也出现问题，最后导致答案错误。我替大家运行过了，是真的（。

所以这个问题，我们一定是使用while的。最后返回ans即可。

我们为什么给ans加的都是right-left+1呢？+1是哪来的？其实很好理解，我们随便举例都能证明这个规律。假设数组[10,5,2,6],k=100，right=0，left=0，如果只计算right-left，那就是0了，但实际上它们代表的子数组[10]明明是符合要求的，应该+1。对于这类**“越短越合法”**的题目，都写的是ans+=right-left+1。下面也放一下灵神对这个部分的解释：

越短越合法
一般要写 ans += right - left + 1。

内层循环结束后，[left,right] 这个子数组是满足题目要求的。由于子数组越短，越能满足题目要求，所以除了 [left,right]，还有 [left+1,right],[left+2,right],…,[right,right] 都是满足要求的。也就是说，当右端点固定在 right 时，左端点在 left,left+1,left+2,…,right 的所有子数组都是满足要求的，这一共有 right−left+1 个。

作者：灵茶山艾府
链接：https://leetcode.cn/discuss/post/0viNMK/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

代码实现

int numSubarrayProductLessThanK(int* nums, int numsSize, int k){
    if(k<=1) return 0;
    int left=0,ans=0,prod=1;
    for(int right=0;right<numsSize;right++){
        prod*=nums[right];
        while(prod>=k){
            prod/=nums[left];
            left++;
        }
        ans+=right-left+1;
    }
    return ans;
}

力扣121.买卖股票的最佳时机

121. 买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

• 1 <= prices.length <= 105
• 0 <= prices[i] <= 104

题目分析

遍历数组时得到最小价格，同时计算最大差（最大利润）。

解题思路

这道题有一个前提：必须买入才能卖出（必须先找最小价格才能算最大利润）。这就暗示我们必须要先找最小价格才能算最大差，并且要在一次遍历里完成。贪心算法的精髓就是找最优，取左最小值，取右最大值。思路有了，实现代码是最重要也是最难的一步。

我们首先对要用到的变量进行初始化。定义最大利润maxProfit=0，最小价格minPrice =prices[0]。这么定义是为了保存一个初始值，在后面判断的时候再更新。接着我们使用for循环遍历数组，先用if判断目前的最小价格是否最小，如果最小则不变，如果不满足则更新目前最小价格值。然后if判断最大利润，如果最大则不变，如果不满足则更新最大利润。最大利润的计算是maxProfit=prices[i]- minPrice，因为我们先前已经更新过最小价格，所以只要满足最大利润判断的prices[i]都是正确的。

将判断过程换成宏定义也可以。即：

#define MAX(a, b) ((a) > (b) ? (a) : (b))

#define MIN(a, b) ((a) < (b) ? (a) : (b))

代码实现

int maxProfit(int* prices, int pricesSize)
{
    int maxProfit = 0;
    int minPrice  =prices[0];
    int i;
    for(i=0; i< pricesSize; i++)
    {
        if(minPrice > prices[i])
            minPrice = prices[i];

        if(prices[i]- minPrice > maxProfit)
            maxProfit=prices[i]- minPrice;
    }
    return maxProfit;

}

力扣20.有效的括号

20. 有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

示例 1：

**输入：**s = “()”

**输出：**true

示例 2：

**输入：**s = “()[]{}”

**输出：**true

示例 3：

**输入：**s = “(]”

**输出：**false

示例 4：

**输入：**s = “([])”

**输出：**true

提示：

• 1 <= s.length <= 104
• s 仅由括号 '()[]{}' 组成

题目分析

用栈记录，遇到左括号让对应右括号入栈，遇到右括号用栈顶元素匹配出栈，最后栈空有效。

解题思路

这道题我们虽然是用栈解决，但是不用额外创建一个栈，只要以字符串s本身为栈就行，可以进行ASCII码的匹配。我们的逻辑就是“消消乐”。由于题目要求括号不能嵌套，必须一一对应，那么就代表 {[]} 应该返回true，但 {[}] 则返回false，我们就只需要看栈顶左括号对应的右括号与入栈的右括号是否一致即可。

在代码的具体实现中，我们首先把top初始化为0。接着我们用for循环遍历字符串s。由于我们要将s作为栈，所以就要定义字符变量c来保存当前遍历到的括号。接着我们用三个if判断来进行入栈，如果 c == ‘(’ 就在栈顶添加 ‘)’ ，如果 c == ‘[’ 就在栈顶添加 ‘]’ ，如果 c == ‘{’ 就在栈顶添加 ‘}’ 。

对左括号的情况判定结束了，下面我们开始处理对右括号的判定。如果遍历到了右括号，我们首先需要判断栈顶是否为空。因为如果栈顶为空的话，就代表这个右括号就已经是无法匹配的了，答案肯定是false。接着还有一种情况，就是栈顶左括号对应的右括号与入栈的右括号不一致的情况。我们写代码的时候一定要注意此时的顺序问题，栈顶先自减再匹配还是先匹配再自减呢？一定是先自减再匹配的。因为top先自减定位到正确栈顶，才能进行匹配。top代表目前栈内的元素个数，但是下标是从0开始的，所以想要查询此时栈顶的元素，一定是要自减的，否则就访问越界了。

最后遍历结束后，判断栈顶是否为空，如果为空就代表匹配有效，返回true，反之返回false。

代码实现

bool isValid(char* s) {
    int top = 0;
    for (int i = 0; s[i]; i++) {
        char c = s[i];
        if (c == '(') {
            s[top++] = ')';
        } else if (c == '[') {
            s[top++] = ']';
        } else if (c == '{') {
            s[top++] = '}';
        } else if (top == 0 || s[--top] != c) {
            return false; 
        }
    }
    return top == 0;
}

力扣23.合并K个升序链表

23. 合并 K 个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[]

提示：

• k == lists.length
• 0 <= k <= 10^4
• 0 <= lists[i].length <= 500
• -10^4 <= lists[i][j] <= 10^4
• lists[i] 按 升序 排列
• lists[i].length 的总和不超过 10^4

题目分析

比较各链表节点，一直查找最小节点，当所有链表均为空，就返回合并后新链表的头结点。

解题思路

做这道题选择了不完全暴力的做法，就是只用遍历所有链表当前的头结点，找出值最小的节点，然后接到新创建的链表尾部，并将对应链表的指针后移，直到所有链表都为空，返回合并后的新链表即可。

我们首先要进行初始化。创建一个虚拟头结点，再创建一个尾指针，始终指向合并链表的尾部，方便直接插入新节点。

接着我们要开始查找最小节点了。用while（1）开始一个一直循环的处理链表的过程。因为题目中可能会有空链表的存在，我们首先用一个for循环定位找到第一个非空链表，如果所有链表都为空，就会通过if判断直接终止循环，返回空。

判断完为空的情况，我们开始在不为空的链表里查找最小节点。我们用if判断逐个比较后续链表的头结点，并用m记录最小值所在的链表索引，方便后续移动指针。

最后更新合并链表，将选中的最小节点链接到结果链表尾部，并移动对应链表的头指针到下一个节点，准备下一轮比较。

通过一次次的循环，我们就得到了合并的新链表，输出虚拟头结点的下一节点即可。

代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize){
    int i = 0, j = 0, m = 0;
    struct ListNode *head = malloc(sizeof(struct ListNode));
    head->next = NULL;
    struct ListNode *tail = head, *min = head;
    while(1){
        for(i = 0; (i < listsSize) && !lists[i]; i++)
        if(i < listsSize){
            min = lists[i];
            m = i;
        }
        else{
            break;
        }
        for(j=i+1; j<listsSize; j++){
            if(lists[j] && (lists[j]->val < min->val)){
                min = lists[j];
                m = j;
            }
        }
        tail->next = min;
        tail = tail->next;
        lists[m] = lists[m]->next;
    }
    return head->next;
}