大数据处理与可视化实验第一课-CSDN博客

本文链接：https://blog.csdn.net/2402_84575086/article/details/146225277

1

# Fixing random state for reproducibility
np.random.seed(19680801) # 设置随机种子，确保每次运行代码时生成的随机数相同，便于结果复现

def gaussian_mixture(x, n=5):
"""Return a random mixture of *n* Gaussians, evaluated at positions *x*."""
def add_random_gaussian(a):
# 生成一个随机的高斯函数并加到数组a上
amplitude = 1 / (.1 + np.random.random()) # 随机生成高斯函数的幅值
dx = x[-1] - x[0] # 计算x的范围
x0 = (2 * np.random.random() - .5) * dx # 随机生成高斯函数的中心位置
z = 10 / (.1 + np.random.random()) / dx # 随机生成高斯函数的宽度参数
a += amplitude * np.exp(-(z * (x - x0))**2) # 将生成的高斯函数加到数组a上

a = np.zeros_like(x) # 初始化一个与x形状相同的零数组
for j in range(n):
add_random_gaussian(a) # 添加n个随机高斯函数到数组a上
return a # 返回生成的高斯混合函数

x = np.linspace(0, 100, 101) # 生成从0到100的101个等间距点
ys = [gaussian_mixture(x) for _ in range(3)] # 生成3个高斯混合函数

fig, ax = plt.subplots() # 创建一个图形和子图
ax.stackplot(x, ys, baseline='wiggle') # 绘制堆叠图，baseline='wiggle'表示基线为波浪线
plt.show() # 显示图形

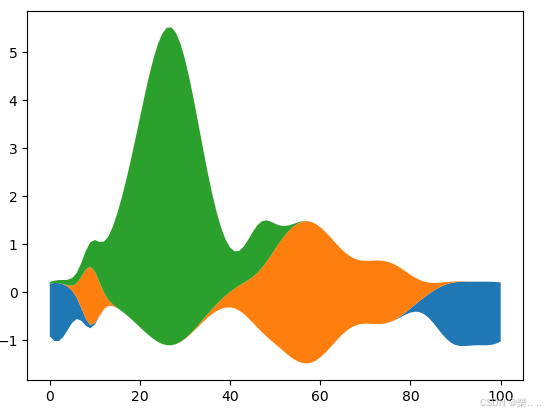
这段代码通过设置随机种子确保结果可复现，利用随机生成的高斯函数模拟灵活的数据分布，并通过堆叠图清晰展示数据的叠加效果，尤其是 `baseline='wiggle'` 增强了波动的动态感。代码结构简洁且模块化，便于扩展和复用，非常适合用于模拟自然现象或实验数据分析。

2

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.cbook as cbook  # 导入matplotlib的工具模块，用于加载示例数据

# 从yahoo的csv数据中加载一个numpy记录数组，包含字段：date, open, high, low, close, volume, adj_close
# 数据来自mpl-data/sample_data目录。记录数组将日期存储为np.datetime64类型，单位为天（'D'）
price_data = cbook.get_sample_data('goog.npz')['price_data']  # 加载Google股票数据
price_data = price_data[-250:]  # 只取最近250个交易日的记录

# 计算每日调整后收盘价的百分比变化：(今日收盘价 - 昨日收盘价) / 昨日收盘价
delta1 = np.diff(price_data["adj_close"]) / price_data["adj_close"][:-1]

# 计算散点图中点的大小，基于交易量数据，归一化到初始交易量的比例，再放大15倍并平方
volume = (15 * price_data["volume"][:-2] / price_data["volume"][0])**2

# 计算散点图中点的颜色，基于收盘价和开盘价的比值
close = 0.003 * price_data["close"][:-2] / 0.003 * price_data["open"][:-2]

# 创建图形和子图
fig, ax = plt.subplots()

# 绘制散点图：
# x轴为今日的百分比变化 (delta1[:-1])，
# y轴为明日的百分比变化 (delta1[1:])，
# 点的颜色由close决定，大小由volume决定，透明度为0.5
ax.scatter(delta1[:-1], delta1[1:], c=close, s=volume, alpha=0.5)

# 设置x轴和y轴标签，使用数学符号表示
ax.set_xlabel(r'$\Delta_i$', fontsize=15)  # x轴：今日变化
ax.set_ylabel(r'$\Delta_{i+1}$', fontsize=15)  # y轴：明日变化

# 设置图表标题
ax.set_title('Volume and percent change')

# 显示网格线
ax.grid(True)

# 自动调整子图布局，避免重叠
fig.tight_layout()

# 显示图形
plt.show()

结果显示

1. 数据加载与处理：
使用 `matplotlib.cbook` 加载示例数据，方便快捷，适合快速验证和实验。通过计算每日股价的百分比变化，能够直观地反映股价的波动性。

2. 散点图的多维度表达：
散点图不仅展示了今日与明日股价变化的关系，还通过点的大小（交易量）和颜色（收盘价与开盘价比值）增加了额外的信息维度，使得图表更加丰富和直观。

3. 可视化细节优化：
通过设置数学符号标签 (`$\Delta_i$`)、网格线和透明度 (`alpha=0.5`)，提升了图表的可读性和美观性，适合用于报告或演示。

4. 金融分析的实用性：
这段代码可以直接应用于金融数据分析，帮助观察股价波动与交易量之间的潜在关系，为投资决策提供参考。

总的来说，这段代码不仅是一个优秀的数据可视化示例，还展示了如何通过简单的数据处理和绘图技巧，从多维度挖掘数据的内在规律。

3

import matplotlib.pyplot as plt
import numpy as np

# 固定随机种子以确保结果可复现
np.random.seed(19680801)

# 定义点的数量
N = 100
# 定义半径阈值
r0 = 0.6

# 生成随机点的x和y坐标，范围在[0, 0.9)之间
x = 0.9 * np.random.rand(N)
y = 0.9 * np.random.rand(N)

# 生成随机点的大小（面积），范围在[0, 400)之间
area = (20 * np.random.rand(N))**2  # 0到10的半径平方
# 生成颜色值，与面积的平方根成正比
c = np.sqrt(area)

# 计算每个点到原点的距离
r = np.sqrt(x ** 2 + y ** 2)

# 根据距离阈值r0，将点分为两个区域：
# area1：距离小于r0的点，使用三角形标记
area1 = np.ma.masked_where(r < r0, area)
# area2：距离大于等于r0的点，使用圆形标记
area2 = np.ma.masked_where(r >= r0, area)

# 绘制距离小于r0的点，使用三角形标记
plt.scatter(x, y, s=area1, marker='^', c=c)
# 绘制距离大于等于r0的点，使用圆形标记
plt.scatter(x, y, s=area2, marker='o', c=c)

# 绘制两个区域的分界线：半径为r0的四分之一圆
theta = np.arange(0, np.pi / 2, 0.01)  # 生成角度值
plt.plot(r0 * np.cos(theta), r0 * np.sin(theta))  # 绘制分界线

# 显示图形
plt.show()