用链表实现多项式的操作

原创于 2025-11-09 20:16:51 发布 · 507 阅读

13 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #c语言

数据结构与算法练习题专栏收录该内容

3 篇文章

订阅专栏

介绍

一个多项式由多项组成，其结构和链表很相似，多项式中每一项对应链表中的每一个节点，这样就可以用链表这一数据结构来描述多项式，用C语言的具体实现如下。

多项式链表实现的类型说明

typedef struct Node *PtrToNode;
struct Node {
    int Coefficient;
    int Exponent;
    PtrToNode Next;
};
typedef PtrToNode Polynomial;

void CreatePolynomial(Polynomial *Poly);
void PrintPolynomial(Polynomial Poly);
Polynomial AddPolynomial(Polynomial Poly1,Polynomial Poly2);
Polynomial MultiplyPolynomial(Polynomial Poly1,Polynomial Poly2);

一个多项式在数据类型上是结构体Node的指针，多项式的每一个项也是结构体Node的指针，每一项包括系数(Coefficient),指数(Exponent)，以及指向下一项的指针(Next)。

创建多项式

void CreatePolynomial(Polynomial *Poly) {
    *Poly=NULL;
    int coef,exp;
    printf("Please enter the polynomial terms(coefficient exponent,enter 0 0 to end):\n");
    while (1) {
        scanf("%d %d",&coef,&exp);
        if (coef==0&&exp==0) {
            break;
        }
        PtrToNode newNode=(PtrToNode)malloc(sizeof(struct Node));
        newNode->Coefficient=coef;
        newNode->Exponent=exp;
        newNode->Next=NULL;
        PtrToNode curr =*Poly;
        PtrToNode prev =NULL;
        while (curr!=NULL&&curr->Exponent>exp) {
            prev=curr;
            curr=curr->Next;
        }
        if (prev==NULL) {
            newNode->Next=*Poly;
            *Poly=newNode;
        }else {
            prev->Next=newNode;
            newNode->Next=curr;
        }
    }
}

一般来说多项式都是按指数降序的，所以在创建多项式时也应对每一项进行排序。这里需要注意的是，CreatePolynomial函数需要传多项式的指针(Polynomial *)。前面说了，虽然Polynomial的数据类型也是一个指针(struct Node *)，但由于这个函数是需要对传进来的多项式进行赋值操作的，如果传的只是Polynomial Poly，这样函数并不会对主函数中的Poly进行赋值。所以这里需要传指向多项式的指针这样的数据类型。

这里通过while循环来进行对多项式每一项的逐次赋值，赋值结束后还需要对每一项按指数的大小进行排序，在第一次循环时，curr和prev此时都是NULL，这样就让刚进行赋值的项的下一项为NULL，再让刚进行赋值的项为第一项。

然后进行第二次赋值，newNode为刚赋值的一项，再进行排序。此时curr是第一项，prev先为NULL，经过while循环后，curr始终是整个多项式中指数比刚赋值项的小一点的项，prev始终是curr的前一项，也就是此时多项式中刚好比curr大一点的项，此时需要做的就是把刚赋值的项插入到prev和curr这两项中间。prev为NULL说明此时多项式中一项都没有，那就让newNode为第一项，其下一项为NULL(代码中也可以把*Poly改成NULL)。如果是一般情况下正常地插入的话，就让pre的下一项指向newNode，让newNode的下一项指向curr，这样就完成了newNode的插入。

打印多项式

void PrintPolynomial(Polynomial Poly) {
    if (Poly==NULL) {
        printf("0\n");
        return;
    }
    PtrToNode p =Poly;
    int isFirst=1;
    while (p!=NULL) {
        if (isFirst) {
            if (p->Coefficient<0) {
                printf("-");
            }
        }else {
            if (p->Coefficient>0) {
                printf("+");
            }else {
                printf("-");
            }
        }
        int absCoef=abs(p->Coefficient);
        if (absCoef!=1||p->Exponent==0) {
            printf("%d",absCoef);
        }
        if (p->Exponent>0) {
            printf("x");
            if (p->Exponent>1) {
                printf("^%d",p->Exponent);
            }
        }
        p=p->Next;
        isFirst=0;
    }
    printf("\n");
}

由于打印一个多项式不需要对多项式的数据进行修改，所以该函数只需传入struct Node *(Ploynomial)类型的数据即可。

由于在创建多项式的时候就已经排好序了，所以在打印多项式时从第一项依次遍历即可。首先处理符号输出，按照多项式的书写形式，第一项如果是正值就不需要正号所以这里声明一个isFirst来控制首项符号的输出，不是第一项的话再通过指数是否大于0来控制正负号的输出，接着先给系数取绝对值，如果系数是±1的话就不输出系数的值，其余情况都输出系数的绝对值。最后看指数部分，如果指数是1的话就不出现^这一符号，其他情况就输出成x^Exponent的形式。一项打印输出完后让p为下一项的指针，然后通过这个while循环把多项式的每一项都打印出来。

多项式相加

Polynomial AddPolynomial(Polynomial Poly1, Polynomial Poly2) {
    Polynomial result=NULL;
    PtrToNode p1=Poly1;
    PtrToNode p2=Poly2;
    PtrToNode last=NULL;
    while (p1!=NULL&&p2!=NULL) {
        if (p1->Exponent==p2->Exponent) {
            int sumCoef=p1->Exponent+p2->Exponent;
            if (sumCoef!=0) {
                PtrToNode newNode=(PtrToNode)malloc(sizeof(struct Node));
                newNode->Coefficient=sumCoef;
                newNode->Exponent=p1->Exponent;
                newNode->Next=NULL;
                if (result==NULL) {
                    result=newNode;
                }else {
                    last->Next=newNode;
                }
                last=newNode;
            }
            p1=p1->Next;
            p2=p2->Next;
        }else if (p1->Exponent>p2->Exponent) {
            if (result==NULL) {
                result=p1;
            }else {
                last->Next=p1;
            }
            last=p1;
            p1=p1->Next;
        }else {
            if (result==NULL) {
                result=p2;
            }else {
                last->Next=p2;
            }
            last=p2;
            p2=p2->Next;
        }
    }
    if (p1!=NULL) {
        last->Next=p1;
    }
    if (p2!=NULL) {
        last->Next=p2;
    }
    return result;
}

由于这个函数的作用的返回Poly1和Poly2两个多项式相加后的结果，不需要修改Poly1和Poly2中的数据，所以传入的数据类型为Polynomial即可。

两个多项式的每俩项相加由三种情况，p1项和p2项的指数次相等，p1项的指数次更大，p2项的指数次更大。

第一种情况，先合并系数，如果系数和0，说明俩项相加抵消了，不进行任何操作。如果系数和不为0，那就创建新节点并进行相关赋值操作。接着再进行核心的尾插操作，让last保持为整个多项式中的最后一项，再将赋值完后的新项尾接到last后，然后再把last赋值为最后一项，最后进行两个多项式的各下一项的相加。

第二种情况，因为p1的指数更大，那么先直接将p1尾插，然后再把last赋值为最后一项，最后进行p1所在的多项式的下一项和p2项进行相加。同理这也是第三种情况的处理方式。

当循环结束时，再进行收尾工作，可能其中有一个多项式留有一部分尾项，再把这个尾项进行尾插即可。

多项式相乘

Polynomial MultiplyPolynomial(Polynomial Poly1, Polynomial Poly2) {
    if (Poly1==NULL||Poly2==NULL) {
        return NULL;
    }
    Polynomial result=NULL;
    PtrToNode p1 =Poly1;
    while (p1!=NULL) {
        PtrToNode p2 =Poly2;
        while (p2!=NULL) {
            int newCoef=p1->Coefficient*p2->Coefficient;
            int newExp=p1->Exponent+p2->Exponent;
            PtrToNode newNode=(PtrToNode)malloc(sizeof(struct Node));
            newNode->Coefficient=newCoef;
            newNode->Exponent=newExp;
            newNode->Next=NULL;
            PtrToNode curr =result;
            PtrToNode prev =NULL;
            while (curr!=NULL&&curr->Exponent>newExp) {
                prev=curr;
                curr=curr->Next;
            }
            if (curr!=NULL&&curr->Exponent==newExp) {
                curr->Coefficient+=newCoef;
                free(newNode);
                if (curr->Coefficient==0) {
                    if (prev==NULL) {
                        result=curr->Next;
                    }else {
                        prev->Next=curr->Next;
                    }
                    free(curr);
                }
            }else {
                if (prev==NULL) {
                    newNode->Next=result;
                    result=newNode;
                }else {
                    prev->Next=newNode;
                    newNode->Next=curr;
                }
            }
            p2=p2->Next;
        }
        p1=p1->Next;
    }
    return result;
}

多项式相乘的思路是让多项式1中的每一项去依次分别乘多项式2中的每一项，然后把相乘得到的结果放到结果多项式中的合适位置，其处理过程和创建多项式的逻辑基本相同。不过可能会出现后乘出来的项与先前已有的项相加为0，那就把这个后乘出来的项free掉，同时把这个在多项式在删除这个先前已有的项再将其free。嵌套while循环结束相乘结果就出来了。

一个实例

int main() {
    Polynomial P1,P2,P3,P4;
    CreatePolynomial(&P1);
    CreatePolynomial(&P2);
    P3=AddPolynomial(P1,P2);
    P4=MultiplyPolynomial(P1,P2);
    PrintPolynomial(P1);
    PrintPolynomial(P2);
    PrintPolynomial(P3);
    PrintPolynomial(P4);
}

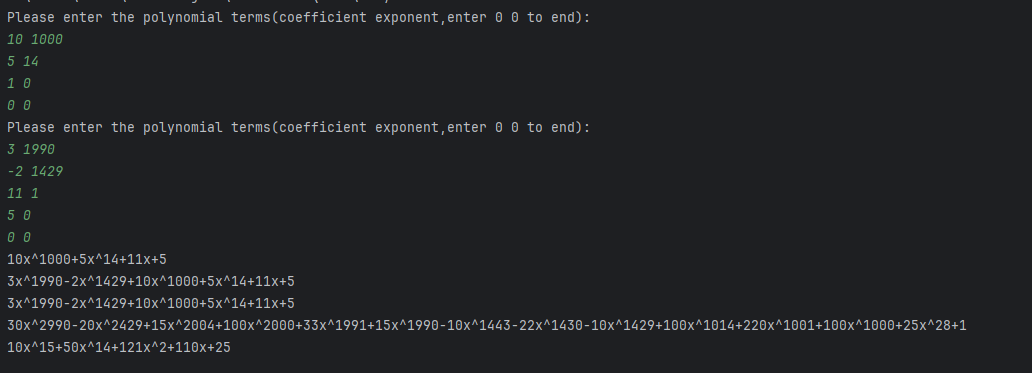
这里给一个例子，P1是 $10x^{^{1000}}+5x^{14}+1$ ,P2是 $3x^{^{1990}}-2x^{1492}+11x+5$ 。其运算结果如下：