【学习笔记】Uncertainty-guided Perturbation for Image Super-Resolution Diffusion Model

( ˶˙⚇˙˶ )୨⚑︎

于 2025-10-06 01:18:53 发布

阅读量330

点赞数 4

CC 4.0 BY-SA版权

文章标签：学习笔记人工智能

本文链接：https://blog.csdn.net/2403_84639931/article/details/152577794

🔹背景概念

在扩散模型 Diffusion Model 或随机微分方程 SDE 框架中：

我们对真实数据（如HR高分辨率图像）反复加入高斯噪声；
训练一个模型学会“去噪”（score estimation），即估计从噪声回到数据分布的梯度方向。

在超分辨率任务SR中：

LR图像（低分辨率）相当于在真实图像分布的低密度区域；
HR图像（高分辨率）在高密度区域；
因此，扩散模型的目标是：学会从LR分布“爬回”HR分布（即生成细节）。

🔹3.1 Noise Levels in Diffusion-based SR — 为什么噪声要“分区间处理”

以往的扩散模型都假设整个图像在每个时刻注入相同水平的噪声 σ(t)（全局同质）。
但作者发现：
不同区域需要不同强度的噪声。

他们做了一个实验：

计算每个像素的残差 (|y - x|)，即上采样后的LR图像 (y) 与对应HR图像 (x) 的差；
- 平坦区域（天空、墙面）→ 残差小；
- 纹理/边缘区域（头发、叶子）→ 残差大。
发现 |y − x| 服从长尾分布，大部分像素差距很小（说明图像大部分区域是平滑的）。
当他们在训练时采用不同噪声上限 σ_max（比如1.0 vs 2.5）：
- 对平坦区（|y−x|小）：几乎不影响输出保真度；
- 对纹理区（|y−x|大）：噪声较大会显著提升感知质量（更锐利、细节更多）；
- 说明“高噪声更适合边缘纹理，低噪声更适合平滑区域”。

结论：
→ 不同区域应使用不同噪声强度：
平坦区（t→0, 高密度）→ 小噪声；
纹理区（低密度）→ 大噪声。

🔹3.2 Uncertainty Estimation — 用“不确定性”量化区域的噪声需求

接下来他们提出了一个衡量每个像素“该不该加大噪声”的指标：不确定性（uncertainty）。

思路：

超分辨率是个病态问题（ill-posed）——特别是在纹理/边缘区域；
在这些区域，重建误差更大、结果更不确定；
因此，用重建残差大小来衡量不确定性。

定义：

令 (x_i) 是HR，(y_i) 是对应LR；
超分模型 (g(y_i)) 生成的SR；
残差越大，说明该区域重建不确定性高；
于是定义不确定性估计为：

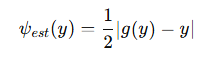
即：
如果 SR 输出与 LR 差别大 → 说明该处信息缺失严重、需要更高噪声；
如果两者几乎相同 → 区域平滑、置信度高、仅需低噪声。

🔹3.3 Uncertainty-guided Noise Weighting (UNW) — 用不确定性指导噪声强度

有了上面的 ψ_est(y)，作者设计了一个自适应噪声权重机制：

定义一个噪声权重系数矩阵 ( w_u(y) )，是一个关于不确定性的单调递增函数：
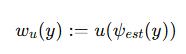
- 不确定性高 → 权重大 → 噪声强；
- 不确定性低 → 权重小 → 噪声弱。
然后在扩散的前向过程和反向过程的分布中引入这个权重：

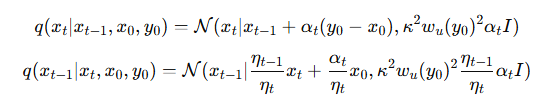
这里的区别就是：噪声协方差项不再是统一的，而是被 (w_u(y_0)) 调制。
这样在扩散过程中：
- 平滑区噪声被“抑制”，保持细节；
- 边缘区噪声被“增强”，促进生成多样性与真实纹理；
- 整个过程更接近真实分布。

他们称整个方法为 UPSR（Uncertainty-guided Perturbation for SR）。

🔹3.4 Network Architecture Modification — 结构优化（提升效率）

原始的扩散模型（如 Stable Diffusion）常用 VQGAN 将图像压缩到潜空间，以降低维度计算。
但：

对SR任务来说，扩散步数较少时，VQGAN的开销反而不划算；
而且LPIPS等感知损失必须在像素域计算，还要多一次解码。

于是他们：

用简单的 PixelUnshuffle 替代VQGAN encoder（快速压缩空间维度）；
用 Nearest Neighbor Upsampling 替代decoder；
保留像素空间操作；
大幅降低显存和计算量，且效果不降。

🔹总结流程图（UPSR整体思路）

1️⃣ 输入 LR 图像 y₀
2️⃣ 用预训练 SR 网络 g(·) 生成初步 SR → 得到 g(y₀)
3️⃣ 计算不确定性： ψ_est(y₀) = ½ |g(y₀) - y₀|
4️⃣ 将其输入单调函数得到噪声权重系数： w_u(y₀)
5️⃣ 在扩散前向/反向过程中，使用 w_u 控制噪声注入
6️⃣ 最后用修改后的扩散模型 fθ 生成最终 HR 图像