数据结构之图的分类和存储

图

图(Graph)G由两个集合V和E组成，记为：G=(V,E)，其中V是顶点的有穷非空集合(其实就是顶点)，E是V 中顶点偶对的有穷集合(就是边)。V(G)和E(G)通常分别表示图G的顶点集合以及边集合，E(G)可以为空集合，但是此时的图只有顶点，没有边。

举个例子：

一个地图： 顶点：城市 边：路 可能只有城市没有路就是E(G)可以为空集合，图只有顶点，没有边。

多个城市 a b c d e

a 到b的方法(a到其他) ：a - b a -c - b a - c - d - b

到a也有很多方法 b-a c-b-a 这样就形成了网状结构

1. 图的分类

• 有向图：

边是有方向的。类似车道的单行道

这意味着每条边都从一个顶点指向另一个顶点，并且这种指向关系是有序的，有向图的 那个方向的线条称为弧。在有向图中，如果有一条从顶点A到顶点B的边，那么我们说A指向B（A是起点，B是终点），但这并不 意味着B也指向A

示例

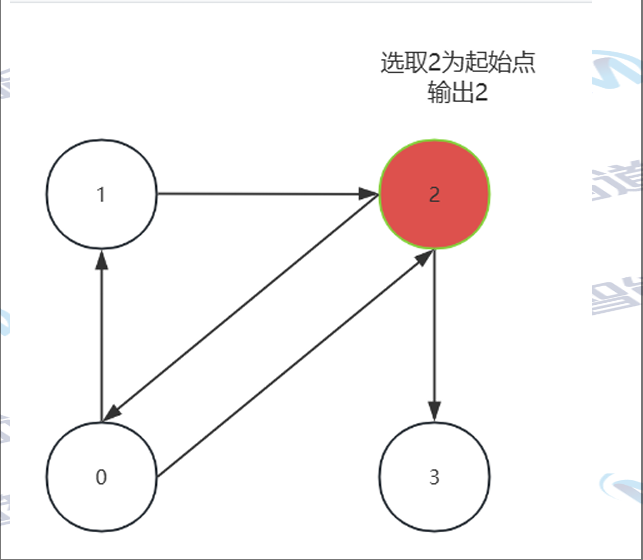
• 无向图：

边没有方向。这意味着每条边都连接两个顶点，但不区分起点和终点。在无向图中，如果两个顶点由一 条边连接，那么它们是相邻的，并且这种相邻关系是对称的。

示例

• 网（带权图）

如果在图的每条边（或者弧）都被赋予一个权重（常用于表示节点之间连接的成本或距离），即为网 （带权图）

顶点的度

表示与顶点相连的边的数量。

• 无向图

• 有向图

在有向图中，顶点的度分为入度（In-degree）和出度（Out-degree）。

入度：指向该顶点的边的数量。

出度：从该顶点出发的边的数量。

• 路径

图的路径是指由图中的顶点和边所构成的序列，其中顶点之间通过边相连。

两个顶点之间存在路径（到达方式），说明它们是连通。

路径可以是有向的或无向 的，这取决于图的类型。

a->c连通 c->a不是因为 这是有向图c到a没有路径到达

若任意两个顶点之间都是连通的话，则图是连通图。

这就是联通图

• 邻接点

邻接点的定义是：如果两个顶点之间存在一条边，那么这两个顶点就互为邻接点

2 图的存储

2.1 邻接矩阵

矩阵（二维数组）

邻接矩阵是表示顶点间相邻关系的矩阵。

对于n个顶点的图，邻接矩阵是一个n×n的二维数组（只存储0 1）。两个顶点存在直接连接到边就是1，否则是0，自己到自己一般也是0

在无向图中，邻接矩阵是对称的（对于对角线对称），而在有向图中则不一定。

• • 无向图

对应的邻接矩阵是

	1	2	3	4	5
1	0	1	0	0	1
2	1	0	0	0	1
3	0	0	0	1	1
4	0	0	1	0	0
5	1	1	1	0	0

• ​
  • 有向图

对应的邻接矩阵是

	1	2	3	4	5
1	0	1	0	0	0
2	1	0	0	0	1
3	0	0	0	0	0
4	0	0	1	0	0
5	1	0	1	0	0

代码如下：

• 有向图：

#include <iostream>
using namespace std;

#define MAX_VERTICES 100 // 最大定点数

// 初始化邻接矩阵  int(*p)[MAX_VERTICES]也可以数组指针
void initalizeGraph(int adjMartix[MAX_VERTICES][MAX_VERTICES], int n)
{
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            adjMartix[i][j] = 0; // 初始化为0，表示没有边
        }
    }
}

// 添加有向边
void addDirectedEdge(int adjMartix[MAX_VERTICES][MAX_VERTICES], int u, int v) // uv是出度也是入度
{
    // 两目标直接连接 有向图
    adjMartix[u][v] = 1;
    // // 无向图
    // adjMartix[v][u]  = 1;
}
void printGraph(int adjMartix[MAX_VERTICES][MAX_VERTICES], int n)
{
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            printf("%d ", adjMartix[i][j]); // 初始化为0，表示没有边
        }
        printf("\n");
    }
}
//  打印图

int main()
{
    int adjMartix[MAX_VERTICES][MAX_VERTICES]; // 图
    // 节点
    int n = 5;
    // 初始化图
    initalizeGraph(adjMartix, n);

    // 添加有向边
    addDirectedEdge(adjMartix, 0, 1);
    addDirectedEdge(adjMartix, 1, 0);
    addDirectedEdge(adjMartix, 1, 4);
    addDirectedEdge(adjMartix, 4, 0);
    addDirectedEdge(adjMartix, 4, 2);
    addDirectedEdge(adjMartix, 3, 2);

    // 打印有向图
    printGraph(adjMartix, n);
    
    return 0;
}

无向图：

#include <iostream>
using namespace std;

#define MAX_VERTICES 100 // 最大定点数

// 初始化邻接矩阵  int(*p)[MAX_VERTICES]也可以数组指针
void initalizeGraph(int adjMartix[MAX_VERTICES][MAX_VERTICES], int n)
{
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            adjMartix[i][j] = 0; // 初始化为0，表示没有边
        }
    }
}

// 添加有向边
void addDirectedEdge(int adjMartix[MAX_VERTICES][MAX_VERTICES], int u, int v) // uv是出度也是入度
{
    // 两目标直接连接 有向图
    adjMartix[u][v] = 1;
    // // 无向图
    adjMartix[v][u]  = 1;
}
void printGraph(int adjMartix[MAX_VERTICES][MAX_VERTICES], int n)
{
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            printf("%d ", adjMartix[i][j]); // 初始化为0，表示没有边
        }
        printf("\n");
    }
}
//  打印图

int main()
{
    int adjMartix[MAX_VERTICES][MAX_VERTICES]; // 图
    // 节点
    int n = 5;
    // 初始化图
    initalizeGraph(adjMartix, n);

    // 添加有向边
    addDirectedEdge(adjMartix, 0, 1);
    addDirectedEdge(adjMartix, 0, 4);
    addDirectedEdge(adjMartix, 1, 4);
    addDirectedEdge(adjMartix, 5, 3);
    addDirectedEdge(adjMartix, 3, 4);

    // 打印有向图
    printGraph(adjMartix, n);
    
    return 0;
}

优点：
编码简单，容易理解。
便于检查图中任意两个顶点之间是否存在边。
便于计算图中顶点的度。
缺点：
对于稀疏图，邻接矩阵会浪费大量存储空间，因为矩阵中的大部分元素都是0。
在进行图的遍历等操作时，可能需要遍历整个矩阵，效率较低。

2.2 邻接表

邻接表是图的一种链式存储结构。对于图中的每个顶点，邻接表都存储一个链表，该链表包含与该顶点相邻的所有顶点。

例如下图1包含和他相邻的所有顶点，2和3

可以省略边：连接关系2-3（隐含表示边）（下节讲，下面的代码不省略）

1 - 2 - 3

1 - 3

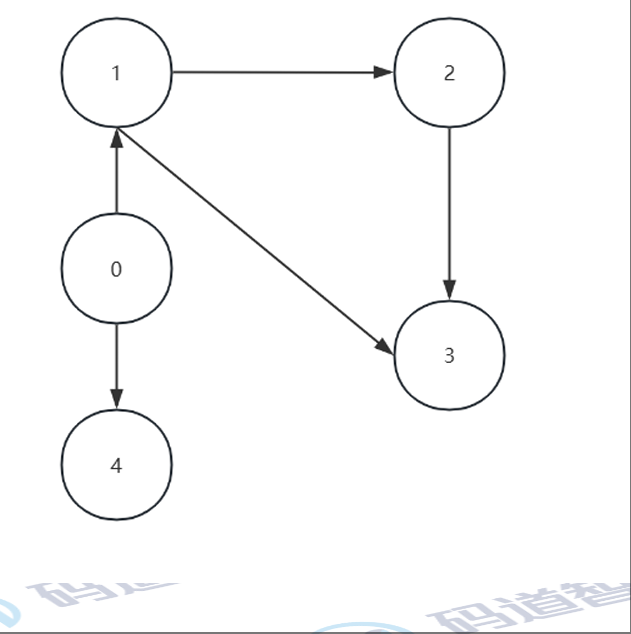
代码如下

#include <iostream>
using namespace std;

// 定义边
typedef struct EdgeNode
{
    int adjvex;            // 邻接点 终点
    struct EdgeNode *next; // 下一条边 个指针用于连接同一起点的多条边。这样，我们就可以通
    // 过遍历next指针来访问从A出发的所有边。
} EdgeNode;

// 定义顶点
typedef struct VertexNode
{
    int data;            // 起点信息
    EdgeNode *FirstNode; // 这个指针用于从顶点出发找到其第一条边 。这样，我们就可以从任意一
    // 个顶点开始，通过firstedge找到其所有邻接点。
} VertexNode;

typedef struct Grasp_List
{
    VertexNode *newNode; // 顶点
    int numVertices;     // 顶点数
    int numEdges;        // 边数
} Grasp_List;

// 初始化函数
void InitGraph(Grasp_List *graph, int n)
{
    graph->newNode = new VertexNode[n](); // 分配内存 ()会进行初始化
    graph->numVertices = n;                顶点5
    graph->numEdges = 0;                  // 边0
    for (int i = 0; i < n; i++)
    {
        graph->newNode[i].data = i;            // 初始化每个顶点的数据
        graph->newNode[i].FirstNode = nullptr; // 初始化第一条边为空
    }
}

// 向图中添加边 u起始顶点 v邻接点
void AddEdge(Grasp_List *graph, int u, int v)
{
    // 创建边
    EdgeNode *newEdgeNode = (EdgeNode *)malloc(sizeof(EdgeNode)); // 创建新边节点
    // 分配失败
    if (!newEdgeNode)
    {
        perror("分配失败");
        return;
    }
    newEdgeNode->adjvex = v; // 设置邻接点 也就是终点
    // 插入 头插法 把边直接
    newEdgeNode->next = graph->newNode[u].FirstNode; // 下一条边=原来的第一条边
    graph->newNode[u].FirstNode = newEdgeNode;       // 更新第一条边
    graph->numEdges++;                               // 边数加1

     如果是无向图 还需要再添加一条边
    // EdgeNode* newNodeV = (EdgeNode*)malloc(sizeof(EdgeNode)); // 创建新边节点
    // if (!newNodeV)
    //{
    //     printf("申请内存失败\n");
    //     exit(-1);
    // }
    // newNodeV->adjvex = u;                     // 设置邻接点
    头插法
    // newNodeV->next = G->adjList[v].firstedge; // 下一条边 = 原来的第一条边
    // G->adjList[v].firstedge = newNodeV;       // 更新第一条边
}

// 打印邻接表
void printGraph(Grasp_List *graph)
{
    if (graph == nullptr)
    {
        cout << "我是空图" << endl;
        return;
    }
    printf("Graph with %d vertices and  %d edge:\n", graph->numVertices, graph->numEdges);
    // 根据定点数遍历
    for (int i = 0; i < graph->numVertices; i++)
    {
        printf("vertices %d: ", graph->newNode[i].data); // 打印顶点
        // 找到顶点第一条边
        EdgeNode *p = graph->newNode[i].FirstNode; // 保存
        while (p)
        {
            // 邻接点
            printf(" %d", p->adjvex);
            // 下一条边
            p = p->next;
        }
        printf("\n");
    }
}

// 释放图占用的内存
void freeGraph(Grasp_List *graph)
{
    if (graph == NULL)
    {
        return;
    }
    // 释放边内存
    for (int i = 0; i < graph->numVertices; i++)
    {
        EdgeNode *curerent = graph->newNode[i].FirstNode;
        EdgeNode *tmp = nullptr;
        while (curerent)
        {
            tmp = curerent;
            curerent = curerent->next;
            free(tmp);
            tmp = nullptr;
        }
        curerent = nullptr;
    }
    // 释放顶点内存
    delete[] (graph->newNode);
    graph->newNode = nullptr;

    // 释放图本身的内存
    delete graph;
}

// 主函数实例
int main()
{

    Grasp_List *G  = new Grasp_List;
    // 初始化图
    InitGraph(G, 5);

    // 添加边
    AddEdge(G, 0, 1);
    AddEdge(G, 0, 4);
    AddEdge(G, 1, 2);
    AddEdge(G, 1, 3);
    AddEdge(G, 2, 3);

    // 打印图
    printGraph(G);

    // 释放图
    freeGraph(G);

    return 0;
}

解释一个遍创建的过程

AddEdge(G, 0, 1);

• 这表示在图 G 中添加一条从顶点 0 到顶点 1 的边。

• 具体步骤如下：

  1. 创建一个新边节点 newEdgeNode，并为其分配内存。
  2. 将新边的邻接点设置为 1。
  3. 使用头插法将新边插入到顶点 0 的边链表中，使新边成为顶点 0 的第一条边。
  4. 图的边数增加 1

• 形成链表的过程

  在调用 AddEdge(G, 0, 1) 后，顶点 0 和顶点 1 通过一条边连接起来。具体来说：

  • 顶点 0 的边链表中新增了一个边节点，其 adjvex 字段为 1。
  • 这个边节点通过 next 指针连接到原来顶点 0 的边链表

优点：
节省存储空间，特别是对于稀疏图。
便于添加和删除边。
便于进行图的遍历等操作。

缺点：
不便于检查图中任意两个顶点之间是否存在边（需要遍历两个顶点的邻接表）。
在某些情况下，可能需要额外的空间来存储顶点的信息（如顶点的索引或名称）。