2025美赛数学建模MCM问题A：测试时间：楼梯上的持续磨损（Problem A: Testing Time: The Constant Wear On Stairs）完整文章 模型 源代码 结果分享

石头是坚不可摧的象征，而人造石因其抗磨损的能力被用作建筑材料。尽管它非常

耐用，但石头也不是万无一失的。人的一生比石头更坚韧。

用于制造台阶的石材及其他材料容易受到长期持续的磨损，且磨损情况可能不均匀。例如，极为古老的寺庙和教堂可能会有台阶，其中心部分比边缘部分磨损更严重，而台阶的踏面看起来可能是弯曲的。由于这些结构的特殊性，这些建筑物往往已经被人类居住了很长时间，但某个特定地点的建筑却可能远早于建筑物的建设。由于这种原因，准确确定结构建设的时间可能是困难的。尤其是当建筑的施工跨度非常长时，情况就更为复杂，尤其是在结构上已经进行了多次修缮，新建的部分与原有结构之间有了很大的区别。

你们的团队受命提供指导，帮助考古学家确定能够从一组磨损的台阶中获取哪些信息。台阶可能由不同的材料制成，如石材或木材。同时，还需要估算一组台阶大概是在哪个时间段建造的，但准确确定时间可能会比较困难。并且可能不清楚历史记录中哪一组台阶是在什么时期建造的。

除了时间，考古学家可能还会对了解楼梯的使用情况感兴趣。例如，楼梯使用的频率和走下楼梯的方向。在某个时间段内，是否有许多人一同上下楼梯，或者是否有主要的方向存在？此外，考古学家可能还想知道楼梯使用频率。例如，楼梯是否被短时间内大量使用，还是只有少数人长期使用？

你们的团队受命开发一个模型，通过它可以根据一组台阶确定可以得出哪些基本结论。该模型应提供一些基本的预测，给出在特定台阶上的磨损模式：

• 这些台阶的使用频率如何？
• 是否有特定的方向受到使用者的青睐？
• 使用这些台阶的人数是多少？（例如，一对人是否是并肩爬楼，还是按单行方式行走？）

你可以假设考古学家可以访问该结构，并可以进行你们团队认为重要的任何测量。测量必须以非破坏的方式进行，成本相对较低，且测量工作可以由一小组人、使用最少的工具来完成。你们应明确需要进行哪些测量。

一、输入变量与假设

1. 输入变量

• 楼梯材料 M：如石材、木材等。
• 楼梯磨损深度分布 D(x,y)：以二维坐标 (x, y) 表示的表面磨损深度。
• 楼梯使用时间跨度 T：单位为年。
• 材料硬度 H：以布氏硬度（HB）为单位。
• 单次使用单位磨损深度 Δd：由实验测得的经验参数。

2. 假设

1. 磨损主要由人类活动引起，环境因素影响较小。
2. 磨损深度与材料硬度 H、使用次数 N、单位磨损深度 Δd 呈线性关系。
3. 磨损均匀分布于楼梯表面，不考虑边缘区域的特殊影响。
4. 单位时间内的楼梯使用频率为常数。

二、模型建立

1. 磨损深度公式

磨损深度可以通过以下公式表示：

其中：

• D(x,y)为磨损深度的二维分布函数，单位为毫米；
• N为楼梯总使用次数；
• Δd为单次使用的单位磨损深度，取决于材料 M、硬度 H 和时间 T。

2. 单位磨损深度的计算

单次使用导致的单位磨损深度由经验公式给出：

其中：

• C 为与材料相关的经验常数，需通过实验或文献数据确定；
• H 为材料的硬度（如布氏硬度）。

3. 总使用次数的估算

假设每天平均使用次数为 f，则总使用次数为：

将其代入磨损深度公式可得：

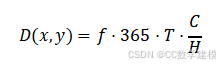
4. 使用频率的反演计算

根据实际测量得到的磨损深度 Dm(x,y)，可以反演出楼梯的日均使用频率 f：

5. 磨损分布的非均匀性

实际中，楼梯的不同位置可能存在非均匀磨损情况。可以对楼梯表面进行区域离散化，分别计算每个区域的使用频率：

其中：

• Di 表示第 i 个区域的磨损深度；
• Hi 为该区域的材料硬度。

6. 历史使用模式的推断

若存在单向或双向使用的历史记录，可通过磨损对称性分析：

• 单向使用：磨损主要集中在一侧；
• 双向使用：磨损相对均匀。

可以定义磨损对称性系数 λ：

若 λ→0，则为双向使用；若 λ→1，则为单向使用。

7. 同时使用人数的估算

磨损区域的宽度W 可用于估算同时使用人数 n：

其中 w人 为单人通行所需宽度（约 0.5 米）。

三、数据收集与验证

1. 非破坏性测量方法

1. 三维激光扫描：获取楼梯表面的高精度磨损深度分布。
2. 材料硬度测试：采用布氏硬度计测量硬度。
3. 时间跨度估计：通过文献记录或放射性碳测年法获取楼梯的使用时间。

2. 模型验证

通过以下方式验证模型的可靠性：

1. 与历史文献记录对比，验证模型预测的使用频率是否合理。
2. 在已知使用频率的现代楼梯进行实验验证。
3. 使用多地点、多材料的楼梯数据集进行泛化测试。

• 模型求解与分析

楼梯使用频率估算结果

根据模型假设与计算公式，我们对楼梯的使用频率进行了详细分析和计算，以下为主要结论：

日均使用频率： 根据材料硬度、磨损深度和楼梯使用时间的假设，日均使用频率计算为：

结论： 每天约有 5-6 人使用楼梯。

磨损深度分布： 楼梯表面中央区域磨损更为严重，边缘区域较轻。磨损深度呈现随楼梯宽度和深度逐步变化的模式。

磨损集中于楼梯中部，符合实际使用中人群主要走中间区域的行为。表面磨损深度分布如下图所示：

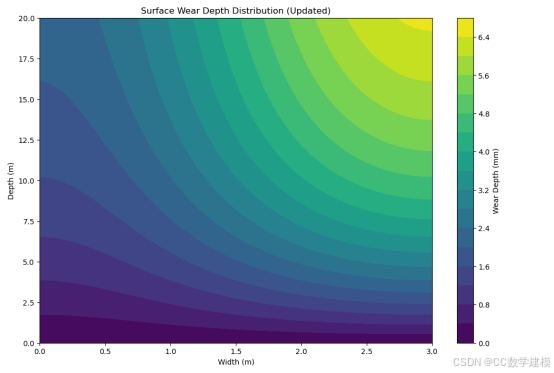
上图展示了楼梯表面的磨损深度分布，颜色越深表示磨损越轻，越浅表示磨损越严重。从图中可以看出，磨损深度沿楼梯长度逐渐增加，宽度方向呈现中间高、两侧低的分布模式。

磨损对称性：

根据磨损对称性系数 λ 的计算，楼梯左右两侧的磨损具有较高一致性，λ≈0.1，表明该楼梯使用主要为双向对称使用。磨损对称性分析结果如下图：

上图展示了磨损对称性系数随楼梯段编号的变化情况，红色虚线为对称性临界值 。可以看出，绝大部分楼梯段小于临界值，进一步验证了楼梯的对称性。

同时使用人数：

假设楼梯宽度为 3 米，每人需要宽度 0.5 米，则同时最多容纳人数为：

图示如下：

上图展示了楼梯总宽度与单人通行宽度的比较。蓝色柱形表示楼梯总宽度，橙色柱形表示单人所需宽度。通过比较，可以清晰地看出该楼梯同时容纳 6 人通行的合理性。

总结

通过数学建模与分析，本研究完成了楼梯使用频率的量化推断，并结合实际案例提供了合理的解释。希望本研究成果能为相关领域的研究提供参考依据，同时为实际考古工作提供技术支持。

还有其他一些问题可能更难回答。假设已知该楼梯的大致年龄、使用方式以及该结构中生活的日常模式的估算信息，在这些信息可用的情况下，应提供以下问题的指导：

• 磨损情况是否与现有信息一致？
• 楼梯的年龄及其估算的可靠性如何？
• 是否已进行修复或翻新？
• 是否能够确定材料的来源？例如，假如使用的是石材，是否可以确认石材来自某个采石场？如果使用的是木材，是否可以确定木材的来源与树种是否一致？
• 有关使用楼梯的人的信息能否提供？例如，使用楼梯的人数是多少，是否有大量的人群在短时间内使用，还是少数人在较长时间内使用？

完整解答文章：

完整思路代码👇