基于matlab对音频信号进行频谱分析并去噪（fir窗函数设计滤波器）

首先，我们需要将选择的音频信号导入matlab并采样为序列，因为现在我们的大多数音频信号是多声道的，因此我们先需要将音频信号转换成单声道（单列序列）来进行下面的操作。

%将双声道音频转换为单列信号
[audioData, sampleRate] = audioread('moon_origin.mp3'); %这里输入你准备的音频信号
singlechannelData=mean(audioData,2);
% audiowrite('moon_single_channel_audio.wav', singlechannelData, 44100);
sound(singlechannelData,44100);

进行上面操作后，我们得到了单列序列singlechannelData，即为我们准备音频信号采样后的序列。

下面，我们对我们的初始音频进行频谱分析。

%绘制信号时域图
t = (0:length(singlechannelData) - 1) / sampleRate;
figure;
plot(t, singlechannelData);
xlabel('t/s');
ylabel('Amplitude');
title('音频信号时域图');

%绘制幅频响应图

%对信号序列进行dft变换并取绝对值
N = length(singlechannelData);
Y = fft(singlechannelData, N);
Y_abs = abs(Y);

%将横坐标转换为频率（hz）
f = (0:N - 1) * sampleRate / N;
%绘制幅频响应图
figure;
plot(f, Y_abs);
xlabel('Frequency/Hz');
ylabel('Amplitude');
title('音频信号幅频响应');

进行以上操作后，我们便能得到原始音频信号的时域图和幅频响应。dft原理不再赘述。

如图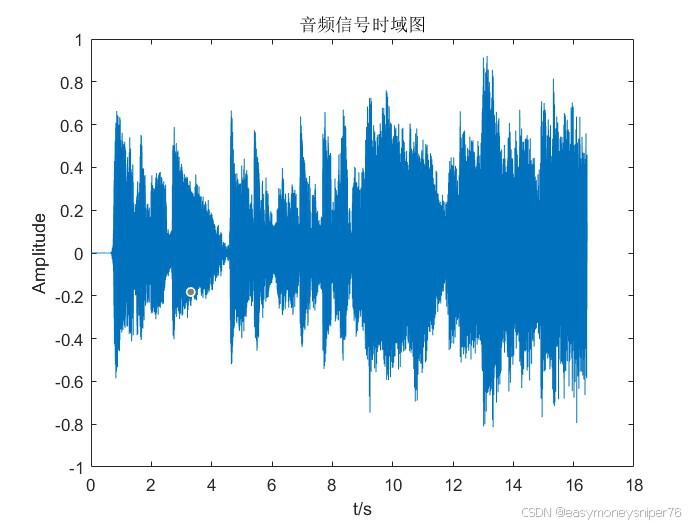

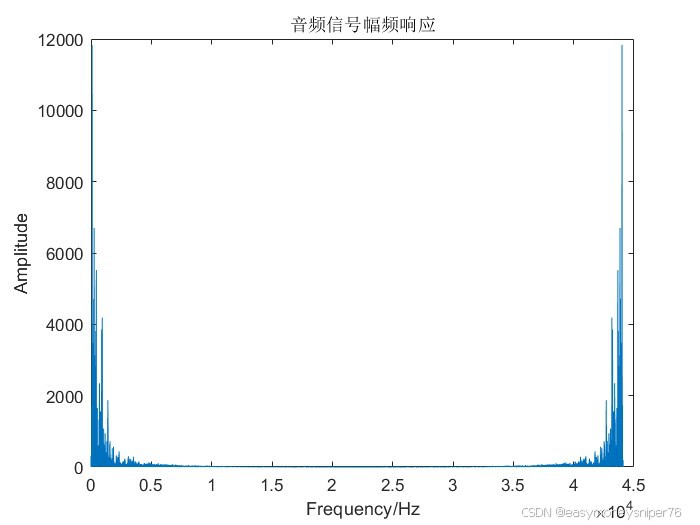
注意，matlab自动生成的幅频响应图像区间为0-fs（0-2pi）。此时我们的幅频响应图是一个以fs/2对称的图形，而在分析中我们仅需看0-fs/2（0-pi）区间即可（因为是以fs/2对称的）。

接着我们模拟产生一个高频噪声信号（以正弦高频噪声信号为例），并将其加入原始音频信号，得到加噪后的噪声信号序列noise，并对其进行频谱分析。

%生成高频正弦信号噪音
t = (0:length(singlechannelData) - 1) / sampleRate; % 时间轴
f_noise = 15000; % 高频噪声频率
A = 0.1; % 噪声幅度
noise = (A * sin(2 * pi * f_noise * t))';

%将噪音加到音频序列中
music_noisy = singlechannelData + noise;
sound(music_noisy,44100);

%绘制加噪后信号时域图
figure;
plot(t, music_noisy);
xlabel('t/s');
ylabel('Amplitude');
title('加噪音频信号时域图');

%对加噪信号进行dft变换
N = length(music_noisy);
Y_noisy = fft(music_noisy, N);
Y_noisy_abs = abs(Y_noisy);
f = (0:N - 1) * sampleRate / N;

%绘制加噪后信号幅频响应图
figure;
plot(f, Y_noisy_abs);
xlabel('Frequency/Hz');
ylabel('Amplitude');
title('加噪音频信号幅频响应');

%将加噪信号保存到电脑
% audiowrite('moon_noise_channel_audio.wav', music_noisy, 44100);
 

得到的加噪后信号noise时域及幅频响应如下

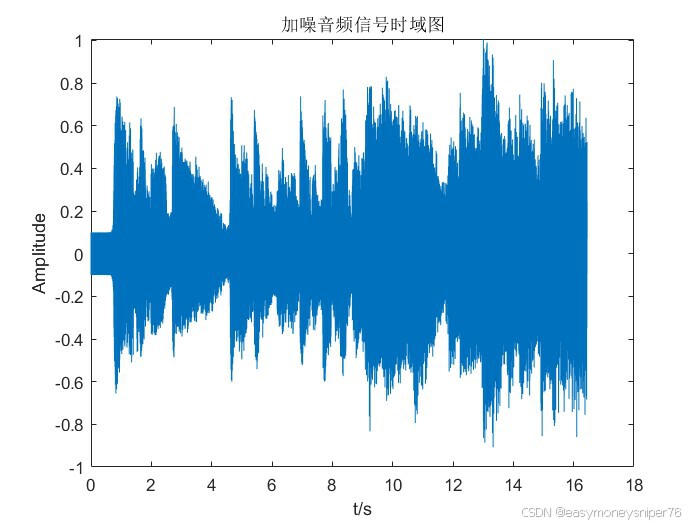
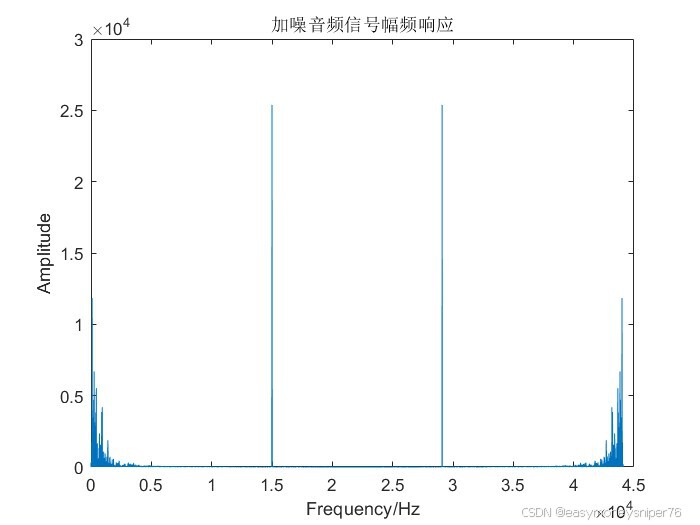
显而易见，与原始音频信号相比，加噪信号多了一个频率为15khz的噪声信号（用来模拟日常中的噪声信号，实际情况更加复杂，这里简化处理，是噪声信号远离主频带，保证滤波后恢复音频信号的质量，减少失真。）并以fs/2对称到右边约30khz处。

根据图易看出，我们需要一个低通滤波器来滤掉这个高频噪声。

使用matlab自带的滤波器designer

我们以fir窗函数的布莱克曼窗设计为例

根据需要设计滤波器的通带截止频率为12000hz，设计好后将滤波器以系数形式导出（方便后面使用filter函数进行滤波）

附滤波器时域图与幅频相频响应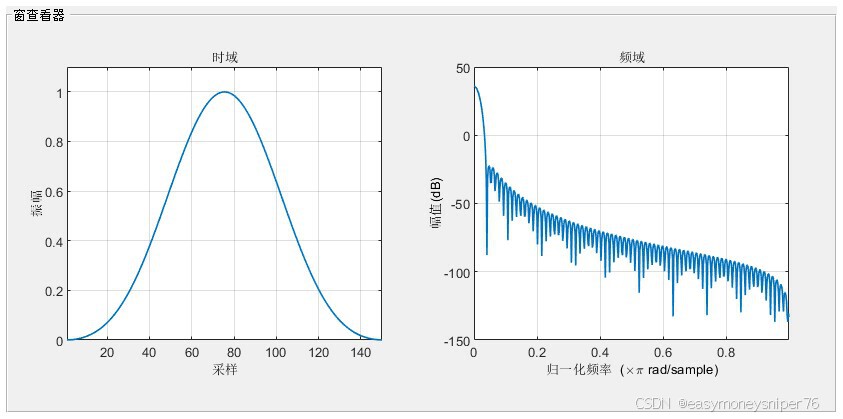

接着我们使用我们设计的滤波器对噪音信号进行滤波处理并进行频谱分析。

% 使加噪信号通过滤波器
remusic=filter(Hd,1,music_noisy);

%绘制通过滤波器后的恢复信号的时域图
t = (0:length(remusic) - 1) / sampleRate;
figure;
plot(t, remusic);
xlabel('t/s');
ylabel('Amplitude');
title('恢复音乐音频信号时域图');

%对信号序列进行dft变换并取绝对值
reN = length(remusic);
reY = fft(remusic, reN);
reY_abs = abs(reY);

%将横坐标转换为频率（hz）
f = (0:N - 1) * sampleRate / N;
%绘制幅频响应图
figure;
plot(f, reY_abs);
xlabel('Frequency/Hz');
ylabel('Amplitude');
title('恢复音频信号幅频响应');

%播放恢复后的音频信号
sound(remusic,44100);

%将恢复的音频保存到电脑
%audiowrite('moon_recover_audio.wav', remusic, 44100);

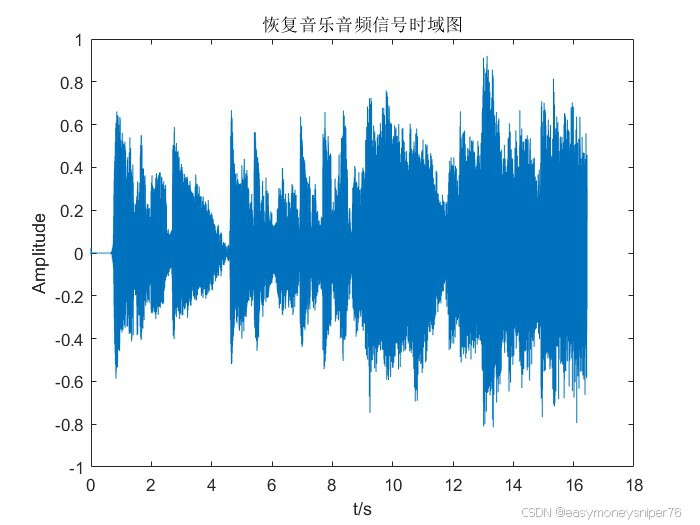
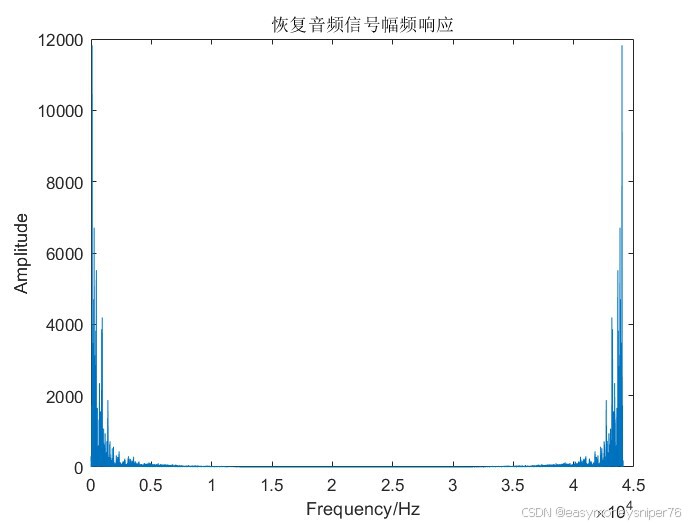
可以看到，我们将15khz的噪音信号滤掉且失真较小。

基于以上所述，我们可以将音频中的远离主频带的噪音信号去除且保证音频失真较小。