至于学习资料,周志华最新的《机器学习》西瓜书已经出了,肯定是首选!以前的话我推荐《机器学习实战》,能解决你对机器学习怎么落地的困惑。李航的《统计学习方法》可以当提纲参考。cs229除了lecture notes,还有session notes(简直是雪中送炭,夏天送风扇,lecture notes里那些让你觉得有必要再深入了解的点这里可以找到),和problem sets,如果仔细读,资料也够多了。
线性回归 linear regression
通过现实生活中的例子,可以帮助理解和体会线性回归。比如某日,某屌丝同事说买了房子,那一般大家关心的就是房子在哪,哪个小区,多少钱一平方这些信息,因为我们知道,这些信息是"关键信息”(机器学习里的黑话叫“feature”)。那假设现在要你来评估一套二手房的价格(或者更直接点,你就是一个卖房子的黑中介,嘿嘿),如果你对房价一无所知(比如说房子是在非洲),那你肯定估算不准,最好就能提供同小区其他房子的报价;没有的话,旁边小区也行;再没有的话,所在区的房子均价也行;还是没有的话,所在城市房子均价也行(在北京有套房和在余杭有套房能一样么),因为你知道,这些信息是有“参考价值”的。其次,估算的时候我们肯定希望提供的信息能尽量详细,因为我们知道房子的朝向,装修好坏,位置(靠近马路还是小区中心)是会影响房子价格的。
其实我们人脑在估算的过程,就类似一个“机器学习”的过程。
a)首先我们需要“训练数据”,也就是相关的房价数据,当然,数据太少肯定不行,要尽量丰富。有了这些数据,人脑可以“学习”出房价的一个大体情况。因为我们知道同一小区的同一户型,一般价格是差不多的(特征相近,目标值-房价也是相近的,不然就没法预测了);房价我们一般按平方算,平方数和房价有“近似”线性的关系。
b)而“训练数据”里面要有啥信息?只给你房子照片肯定不行,肯定是要小区地点,房子大小等等这些关键“特征”
c)一般我们人肉估算的时候,比较随意,也就估个大概,不会算到小数点后几位;而估算的时候,我们会参照现有数据,不会让估算跟“训练数据”差得离谱(也就是下面要讲的让损失函数尽量小),不然还要“训练数据”干嘛。 计算机擅长处理数值计算,把房价估算问题完全可以用数学方法来做。把这里的“人肉估算”数学形式化,也就是“线性回归”。
1.我们定义线性回归函数(linear regression)为:
然后用h(x) 来预测y
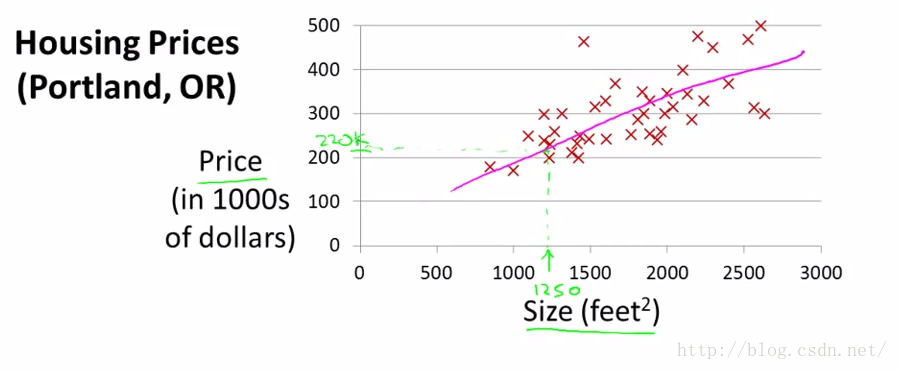
最简单的例子,一个特征size,y是Price,把训练数据画在图上,如下图。(举最简单的例子只是帮助理解,当特征只有一维的时候,画出来是一条直线,多维的时候就是超平面了)
这里有一个问题,如果真实模型不是线性的怎么办?所以套用线性回归的时候是需要预判的,不然训练出来的效果肯定不行。这里不必过于深究,后面也会介绍怎么通过预处理数据处理非线性的情况。
2.目标就是画一条直线尽量靠近这些点,用数学语言来描述就是cost function尽量小。
为什么是平方和? 直接相减取一下绝对值不行么, | h(x)-y | ? (后面的Probabilistic interpretation会解释,这样求出来的是likelihood最大。另外一个问题, | h(x)-y |大的时候 ( h(x)-y )^2 不也是一样增大,看上去好像也一样?! 除了后者是凸函数,好求解,所以就用平方和? 不是的,单独一个样本纵向比较确实一样,但别漏了式子前面还有一个求和符号,这两者的差异体现在样本横向比较的时候,比如现在有两组差值,每组两个样本,第一组绝对值差是1,3,第二组是2,2,绝对值差求和是一样,4=4, 算平方差就不一样了,10 > 8。其实,x^2求导是2x,这里的意思就是惩罚随偏差值线性增大,最终的效果从图上看就是尽可能让直线靠近所有点)
3 然后就是怎么求解了。
如果h(x)=y那就是初中时候的多元一次方程组了,现在不是,所以要用高端一点的方法。以前初中、高中课本也有提到怎么求解回归方程,都是按计算器,难怪我一点印象都没有,囧。。还以为失忆了
notes 1里面介绍3种方法
1.gradient descent (梯度下降)
a.batch gradient descent
b.stochastic gradient descent (上面的变形)







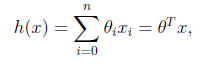
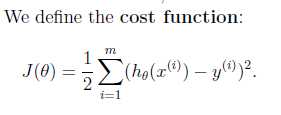
















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








