科研小白也能搞懂的机器学习！！！-CSDN博客

本文链接：https://blog.csdn.net/2501_91695155/article/details/147445574

机器学习是一门通过数据学习规律并进行预测与分析的学科，其核心在于通过数学模型对数据进行建模，并利用算法优化模型参数，使其满足学习目的。

机器学习的实现包含三个关键要素：模型（Model）、策略（Strategy）和算法（Algorithm）。

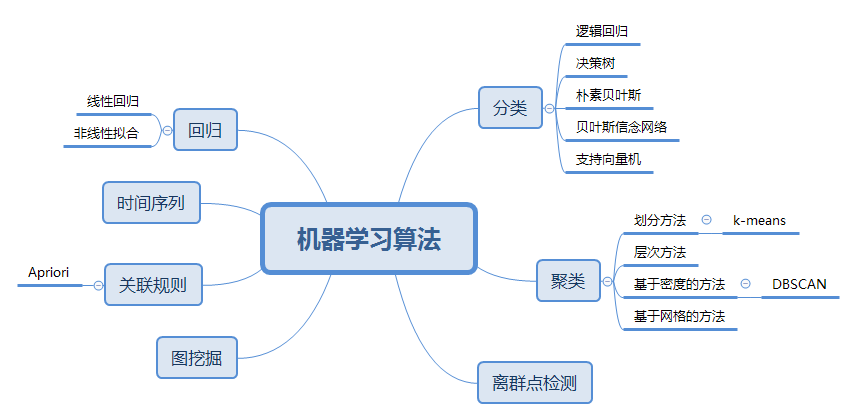
模型定义了输入与输出之间的映射关系，是机器学习的基础。

它源自一个称为假设空间的集合，例如线性回归模型假设目标变量是输入的线性组合，而神经网络则能建模复杂的非线性关系。模型选择对学习效果具有决定性影响。

在这里列举几个常见的模型：

随机森林

由多个决策树组成的集成模型。在训练时，从原始训练数据中有放回地抽样生成多个子集，分别训练决策树，然后通过投票或平均等方式综合多个决策树的结果进行预测。随机森林能够有效降低模型的过拟合风险，提高模型的泛化能力。

卷积神经网络（CNN）

主要用于处理图像、视频等具有网格结构的数据。它通过卷积层、池化层和全连接层等组件，自动提取数据的特征。卷积层中的卷积核在数据上滑动，提取局部特征，池化层则用于压缩数据维度，减少计算量。CNN 在图像识别、目标检测等领域取得了巨大的成功。

循环神经网络（RNN）

适用于处理序列数据，如文本、语音等。它能够对序列中的每个元素进行处理，并将当前的输出与之前的状态信息相结合，从而捕捉序列中的长期依赖关系。

由于其在处理序列数据方面的局限性，后来又发展出了长短时记忆网络（LSTM）和门控循环单元（GRU）等改进型的循环神经网络，它们能够更好地处理长序列数据中的信息。

一个简单的RNN结构示例

# 一个简单的RNN结构示例class SimpleRNN(nn.Module):    def __init__(self, input_size, hidden_size):        super(SimpleRNN, self).__init__()        self.rnn = nn.RNN(input_size, hidden_size, batch_first=True)    def forward(self, x):        out, _ = self.rnn(x)        return out

聚类模型

其中K-Means 聚类大家更熟悉，它将数据点划分为 K 个簇，使得每个数据点属于与其距离最近的簇中心所在的簇。算法通过不断迭代更新簇中心，直到簇的划分不再变化或达到预设的迭代次数。

K-Means 聚类是一种简单且常用的聚类算法，可用于客户细分、图像分割等领域。

算法

是一种常用的优化算法，通过计算损失函数关于模型参数的梯度，沿着梯度的反方向更新参数，以逐步减小损失函数的值。

梯度下降算法

随机梯度下降（SGD）是其变体，每次使用一个样本进行梯度计算和参数更新，而批量梯度下降（BGD）则使用整个训练数据集计算梯度。小批量梯度下降（MBGD）则介于两者之间，使用一小部分样本进行计算。

梯度下降法可以类比为一个人从山上下山的过程。假设一个人被困在山上，需要找到一条路径下山到达山谷。由于山上浓雾很大，可视度很低，这个人无法一眼看到下山的路径，因此他需要在当前位置寻找最陡峭的下坡路，然后沿着这个方向走一段距离。每走一段距离后，他会重新评估并寻找新的最陡峭的下坡路，如此反复，直到到达山谷。在这个过程中，最陡峭的下坡路对应于梯度下降法中的梯度方向，而走的每一步对应于梯度下降法中的一次迭代。

代码：

import numpy as npimport matplotlib.pyplot as plt# 生成一些示例数据np.random.seed(0)X = 2 * np.random.rand(100, 1)y = 4 + 3 * X + np.random.randn(100, 1)# 初始化参数w = 0b = 0# 定义超参数learning_rate = 0.01num_iterations = 1000n = len(X)# 梯度下降算法for iteration in range(num_iterations):    # 计算预测值    y_pred = w * X + b    # 计算梯度    dw = (2 / n) * np.sum((y_pred - y) * X)    db = (2 / n) * np.sum(y_pred - y)    # 更新参数    w = w - learning_rate * dw    b = b - learning_rate * db    # 每100次迭代打印一次损失值    if iteration % 100 == 0:        loss = (1 / n) * np.sum((y_pred - y) ** 2)        print(f'Iteration {iteration}: Loss = {loss}')print(f'Final parameters: w = {w}, b = {b}')# 绘制原始数据和拟合直线plt.scatter(X, y)plt.plot(X, w * X + b, color='red')plt.xlabel('X')plt.ylabel('y')plt.title('Gradient Descent for Linear Regression')plt.show()

运行结果：

反向传播算法

主要用于神经网络的训练，它通过计算损失函数关于网络各层参数的梯度，从输出层反向传播到输入层，来更新参数。反向传播算法使得神经网络能够高效地进行训练，是深度学习发展的关键技术之一。

代码：

import numpy as np# 定义sigmoid激活函数及其导数def sigmoid(x):    return 1 / (1 + np.exp(-x))def sigmoid_derivative(x):    return x * (1 - x)# 输入数据集X = np.array([[0, 0, 1],              [0, 1, 1],              [1, 0, 1],              [1, 1, 1]])# 输出数据集y = np.array([[0], [1], [1], [0]])# 随机初始化权重np.random.seed(1)syn0 = 2 * np.random.random((3, 4)) - 1syn1 = 2 * np.random.random((4, 1)) - 1# 训练迭代次数epochs = 60000for j in range(epochs):    # 前向传播    l0 = X    l1 = sigmoid(np.dot(l0, syn0))    l2 = sigmoid(np.dot(l1, syn1))    # 计算输出层的误差    l2_error = y - l2    # 每10000次迭代打印一次误差    if (j % 10000) == 0:        print("Error:" + str(np.mean(np.abs(l2_error))))    # 计算输出层的误差梯度    l2_delta = l2_error * sigmoid_derivative(l2)    # 计算隐藏层的误差    l1_error = l2_delta.dot(syn1.T)    # 计算隐藏层的误差梯度    l1_delta = l1_error * sigmoid_derivative(l1)    # 更新权重    syn1 += l1.T.dot(l2_delta)    syn0 += l0.T.dot(l1_delta)print("Output After Training:")print(l2)