函数递归详解（含汉诺塔动图演示）

函数递归详解（含汉诺塔动图演示）

---

一、什么是递归？

递归（Recursion）是程序设计中非常经典的一种思想。简单来说，递归就是函数调用它自己。

递归的核心思想是：

把一个大问题转化为规模较小、形式相似的子问题，再逐步求解，直到问题不可再分。

例如：

#include <stdio.h>

int test() 
{
    printf("hehe\n");
    test(); // test函数中再次调用 test 函数
    return 0;
}

虽然这段代码能展示“函数调用自己”，但它没有终止条件，会导致死递归和栈溢出 (Stack Overflow)。
所以在编写递归函数时，必须控制递归的深度和出口。

---

二、递归的两个必要条件

1. 必须存在终止条件（即边界条件）
   当满足该条件时，递归停止。
2. 每一次递归都要让问题更接近终止条件
   否则会无限循环。

这两个条件是编写递归函数的关键。

---

三、递归经典示例

示例 1：计算 n 的阶乘

数学定义： n！ = n × (n - 1)！

当 n = 1 时，n！= 1。

代码实现：

int Fact(int n) 
{
    if (n <= 0)
        return 1;
    else
        return n * Fact(n - 1);
}

递归过程分析（以 Fact(5) 为例）：

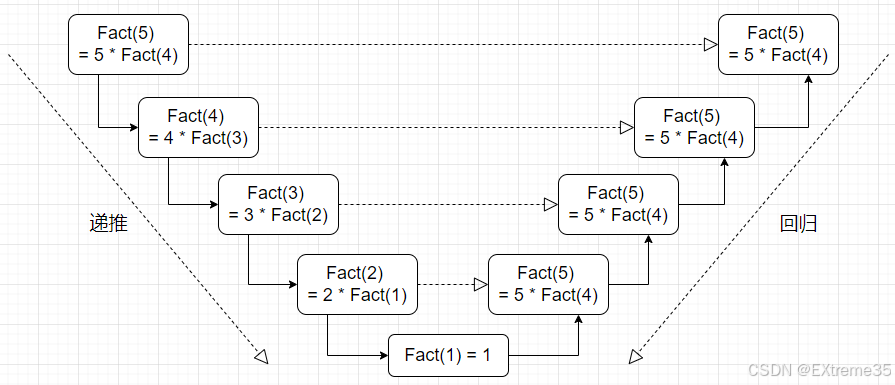
Fact(5)
= 5 * Fact(4)
= 5 * 4 * Fact(3)
= 5 * 4 * 3 * Fact(2)
= 5 * 4 * 3 * 2 * Fact(1)
= 5 * 4 * 3 * 2 * 1

---

示例 2：顺序打印整数的每一位

需求：
输入整数 1234，按顺序输出 1 2 3 4

递归分析：

• 若 n > 9，先打印 n / 10 的各位；
• 然后再打印当前最后一位 n % 10。

代码实现：

void Print(int n) 
{
    if (n > 9)
        Print(n / 10);
    printf("%d ", n % 10);
}

执行流程（以 Print(1234) 为例）：

Print(1234)
→ Print(123)
→ Print(12)
→ Print(1)
→ 打印 1 → 打印 2 → 打印 3 → 打印 4

---

四、递归与迭代的比较

递归虽然简洁优雅，但也存在一定的性能开销。
在每次函数调用时，系统都会为该函数分配栈帧，用于保存局部变量和返回地址。
如果递归层数过多，会造成 栈溢出 (stack overflow)。

例如计算斐波那契数列：

int Fib(int n) {
    if (n <= 2)
        return 1;
    else
        return Fib(n-1) + Fib(n-2);
}

当输入 Fib(40) 时，重复计算次数极多，效率极低。

而迭代方式的效率更高：

int Fib(int n) 
{
    int a = 1, b = 1, c = 1;
    while (n > 2) 
    {
        c = a + b;
        a = b;
        b = c;
        n--;
    }
    return c;
}

总结：

• 当问题结构清晰、规模适中时，递归可简化逻辑。
• 当问题规模较大时，优先考虑迭代（循环）以提高效率。

---

五、递归进阶：汉诺塔问题（Hanoi Tower）

问题描述：
有三根柱子 A、B、C，A 柱上有若干不同大小的圆盘，要求将所有圆盘从 A 移动到 C，且：

1. 一次只能移动一个圆盘；
2. 大圆盘不能压在小圆盘上；
3. 可以借助中间的柱子 B。

1、当只有一个盘子时，直接移动
2、当有两个盘子时，先将上面的盘子挪走，但不要占目的位置，然后将最大的放至目的位置，再将次小的放在目的位置
3、有三个及以上的盘子的时候，一步一步推有点慢，可以从之前的移动中找规律，可以发现每次都是将最大的盘子上面所有的盘子，移至一个既不是初始位置也不是目的位置的柱子上，然后直接将最大的盘子一步到位，剩下的也是如此。

只不过需要注意的是假设刚开始有ABC三个柱子，将除最大盘子外的所有盘子挪到中转柱子时，此时中转柱子是第二个柱子，也就是B柱子，但如果继续挪次大的盘子，此时的中转柱子，就成了A柱子。
这里有点绕，后面有四层汉诺塔的动图，可以结合看一下

递归思路：

1. 先将 n-1 个盘从 A → B；
2. 再将最大的盘从 A → C；
3. 最后将 n-1 个盘从 B → C。

递归函数定义：

这里需要多想一下函数的三个柱子参数，可以简单理解为，第一个参数就是有很多盘子的柱子，第二个参数就是中转柱子，第三个参数就是目的柱子。不要被参数名误导！

个人理解，不对可以留言。

//打印移动路径
void print(char start, char end)
{
	printf("%c->%c ", start, end);
}
//递归函数思路
void Hanoi(int n, char start, char transfor, char end)
{
	if (n == 1)
		print(start, end);
	else
	{
		//将除底部盘子外的所有盘子借助目的柱子转移到中转柱子上
		Hanoi(n - 1, start, end, transfor);
		//将底部盘子挪至目的柱子上
		print(start, end);
		//将中转柱子上的其余盘子借助起始柱子挪至目的柱子上
		Hanoi(n - 1, transfor, start, end);
	}
}

测试代码：

int main()
{
	Hanoi(1, 'A', 'B', 'C');
	printf("\n");
	Hanoi(2, 'A', 'B', 'C');
	printf("\n");
	Hanoi(3, 'A', 'B', 'C');

	return 0;
}

输出示例（前 3 层汉诺塔）：

---

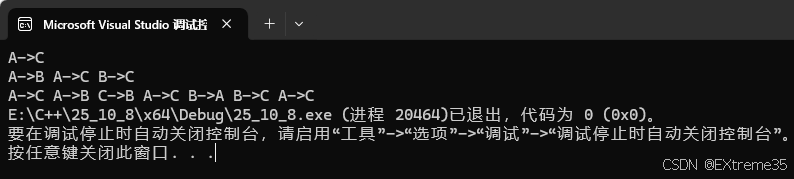
六、汉诺塔递归动图演示（3层和4层）

1、三层汉诺塔递归效果演示：

2、四层汉诺塔递归效果演示：

这里就可以看出当黄色盘子挪到目的地后，空出来的柱子也就成了A柱而不是B柱。

---

七、总结

优点	缺点
思路清晰，代码简洁	占用栈空间多
适合分解型问题	可能造成栈溢出
容易表达数学递推关系	性能不如迭代

递归的关键是：

找到终止条件 + 明确子问题的缩小路径

掌握了这两点，你就能轻松实现如阶乘、斐波那契、汉诺塔等各种递归问题。

---