着装规范识别程序报告（决策树算法）-CSDN博客

本文链接：https://blog.csdn.net/2502_90436524/article/details/147353729

一.问题描述和需求分析

1.背景以及问题的提出

相信大家上小学的时候就天天有校门口红领巾，校服等着装规范的检查，而现在好像部分外卖平台的外卖员也需要进行一些着装规范的检查，比如有没有穿戴对应平台所需要穿戴的冲锋衣，有没有面带微笑等规范。这两者的区别在于，我们小时候对红领巾（即少先队员的着装）的检查是由小队长，中队长，也就是人工检查，这样就需要小朋友一大早就起床守在校门口检查。而现在外卖平台的检查就是用AI进行快速的图像识别检查。（本报告不至于做到完整的图像识别加分析，不过后端的算法部分是可以实现的）

在某些商业环境中，缺乏明确的着装规定，仅有一个大致而模糊的衣着标准。这种时候，金融公司的小白就会纠结于服装搭配。怎么解决呢？肯定得看老前辈们的搭配来学习，但是看了一圈总感觉眼花缭乱，找不到合适的标准。在这种情况下，单纯依赖传统算法显然是不够的。例如，现代大酒店通常会使用安保人员来识别那些“衣冠不整”的客人。实际上，这些任务完全可以通过人工智能来执行。

此外，AI在着装规范识别上的应用还可以扩展到公共安全领域。在一些重要的公共活动中，通过AI系统对参与者进行着装检查，可以有效预防不安全因素的出现，保障活动的顺利进行。例如，在大型体育赛事或演唱会中，AI可以快速识别出携带违禁物品或穿着不当的观众，从而提前采取措施。

图1 人脸识别匝机外貌

那么如何才能实现，或者说应该运用什么样的算法来实现这样的功能呢？我想，决策树就是一个很好的解决问题的思路。

2.决策树的介绍：

决策树（Decision Tree）在机器学习中是一个很常见的算法，像很多有关决策的问题其实都可以用它来求解。

它通过一系列的规则来对数据进行分类，这些规则以树状结构呈现，每个节点代表一个属性上的判断，而每个分支则代表一个判断结果的输出。在构建决策树时，算法会尝试找到最佳的属性分割点，以使得数据集的分类效果最好。

决策树算法的核心在于递归地选择最优特征，并根据该特征对样本集进行分割，使得对子集进行分类时，能够达到最大的信息增益。信息增益是基于熵的概念，熵是度量数据集纯度的一种方式。通过减少熵值，决策树能够有效地将数据集分割成更纯净的子集，从而提高分类的准确性。

在实际应用中，决策树算法因其直观、易于理解和解释而受到青睐。它不仅可以处理数值型数据，还能很好地处理类别型数据。此外，决策树模型在处理缺失数据和异常值方面也具有一定的鲁棒性。然而，决策树也存在一些局限性，比如容易过拟合，即在训练数据上表现很好，但在未见过的数据上泛化能力较差。为了克服这一问题，通常会采用剪枝技术，或者使用集成学习方法，如随机森林和梯度提升树等。

图2 决策树的树状演示图

需求分析：

本报告以某证券公司的着装规范为具体示例，深入浅出地展示了着装规范分析的应用场景与重要性。然而，值得强调的是，通过技术创新，我们已经成功地将这一分析框架从一个静态的、特定领域的示例，转变为一个高度动态、灵活且可广泛应用的交互式系统。这一转变的核心在于，系统的输入端被精心设计为一个直观易用的交互式界面，允许在运行时根据实际需求即时输入不同的分析样例。

这种设计思路的巧妙之处在于，它赋予了系统无与伦比的灵活性和高度的可移植性。无论是对企业员工的职业着装要求，还是对特定团体如少先队员的着装规范进行分析，系统都能轻松应对。以少先队员的着装规范为例，虽然传统上我们可能认为这仅仅涉及佩戴红领巾和穿着统一的校服，但现实生活中的情况远比这复杂。不同地区、不同学校甚至不同活动场合，少先队员的着装都可能有所差异。通过我们的交互式系统，用户可以轻松输入这些多样化的场景，系统则能够迅速生成相应的着装规范分析报告，为决策提供有力支持。

更为重要的是，这一系统的潜力远不止于此。它同样可以应用于更为广泛的社会调研领域。想象一下，通过收集和分析大量数据，系统能够揭示出在不同场合下人们更倾向于穿着哪些类型的服饰。这些信息对于计划前往这些场合的人士来说无疑具有极高的参考价值。无论是商务洽谈、休闲聚会还是重要庆典，系统都能根据历史数据和当前趋势，为用户推荐最合适的着装方案。

从市场需求的角度来看，这一系统的应用前景无疑是非常广阔的。在当今这个日新月异的时代，人们对于着装的要求越来越高，也越来越多样化。一个能够根据不同场合、不同需求自动生成着装建议的系统，无疑将受到广大用户的热烈欢迎。而要实现这一目标，就需要系统具备强大的自学习能力。通过不断的学习和优化，系统能够逐渐积累起丰富的经验和知识，从而更加精准地满足用户的需求。

由此看出，其实需求很多，市场很大。而具体的需求就是能够实现无人参与情况下的自学习然后快速的做出决策，即生成一个树，来进行一个类似于经验总结的作用。

二.算法原理和技术路线

1.决策树算法原理

决策树算法是一种基本的分类与回归方法，其模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以被认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。决策树的主要优点是模型具有可读性，分类速度快。学习时，利用训练数据，根据损失函数最小化的原则建立决策树模型。预测时，对新的数据，利用决策树模型进行分类。

决策树学习通常包括三个步骤：特征选择、决策树的生成和决策树的修剪。目标是根据给定的训练数据集构建一个决策树模型，使它能够对实例进行正确的分类。决策树学习本质上是从训练数据集中归纳出一组分类规则。在选择决策树时，应选择一个与训练数据矛盾较小的决策树，同时具有很好的泛化能力；而且选择的条件概率模型应该不仅对训练数据有很好的拟合，而且对未知数据有很好的预测。

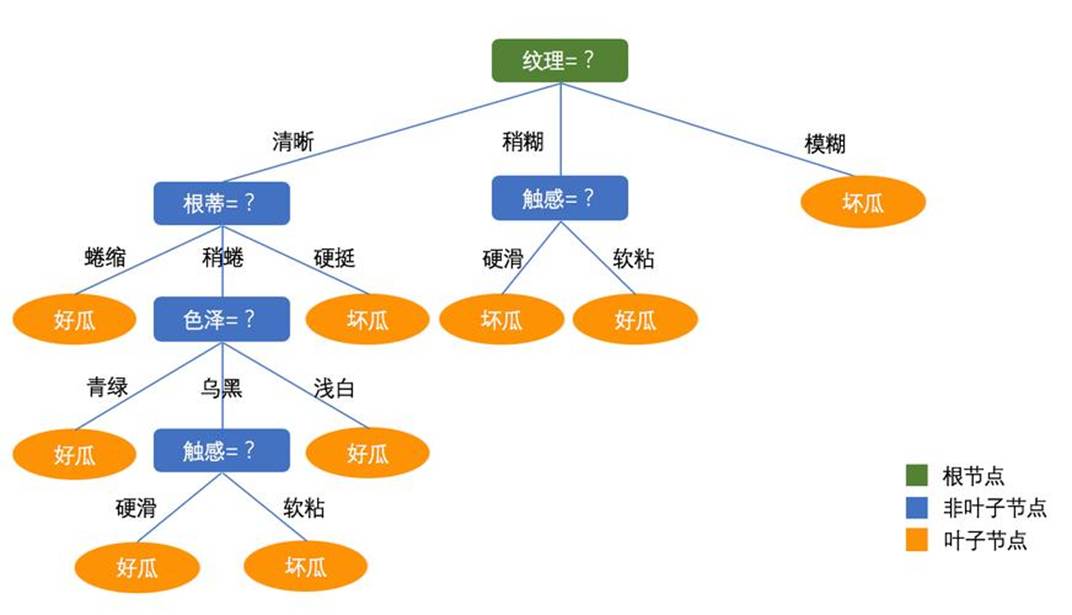
图3 周志华西瓜书上带例子的决策树

损失函数通常是正则化的极大似然函数，策略是以损失函数为目标函数的最小化。因为从所有可能的决策树中选取最优决策树是NP完全问题，所以现实中决策树学习通常采用启发式方法，近似求解这一最优化问题，得到的决策树是次最优的。

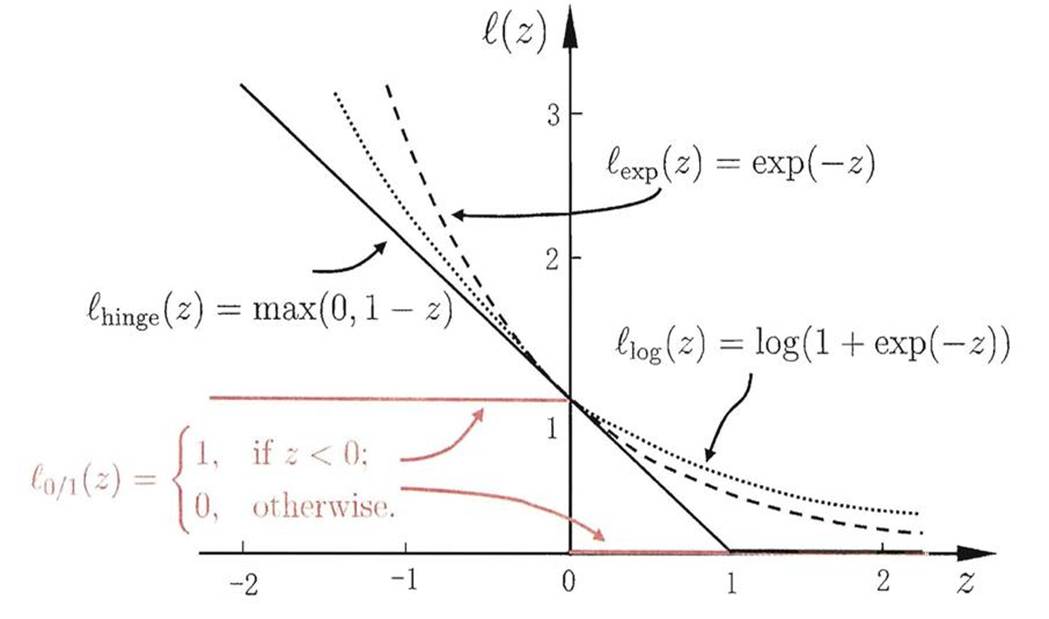
图4 几种损失函数函数图

决策树学习的算法通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割，使得对各个子数据集有一个最好的分类的过程。包含特征选择、决策树的生成和决策树的剪枝过程。剪枝的目的是将树变得更简单，从而使它具有更好的泛化能力。步骤包括去掉过于细分的叶结点，使其回退到父结点，甚至更高的结点，然后将父结点或更高的结点改为新的叶结点。

特征选择是决策树学习开始时对特征进行选择，只留下对训练数据有足够分类能力的特征。决策树的典型算法有ID3，C4.5，CART等。

决策树算法的优点包括分类精度高、生成的模式简单、对噪声数据有很好的健壮性，因而是目前应用最为广泛的归纳推理算法之一，在数据挖掘中受到研究者的广泛关注。

决策树构造的输入是一组带有类别标记的例子，构造的结果是一棵二叉树或多叉树。二叉树的内部节点一般表示为一个逻辑判断，树的边是逻辑判断的分支结果。多叉树的内部结点是属性，边是该属性的所有取值，有几个属性值就有几条边。树的叶子节点都是类别标记。

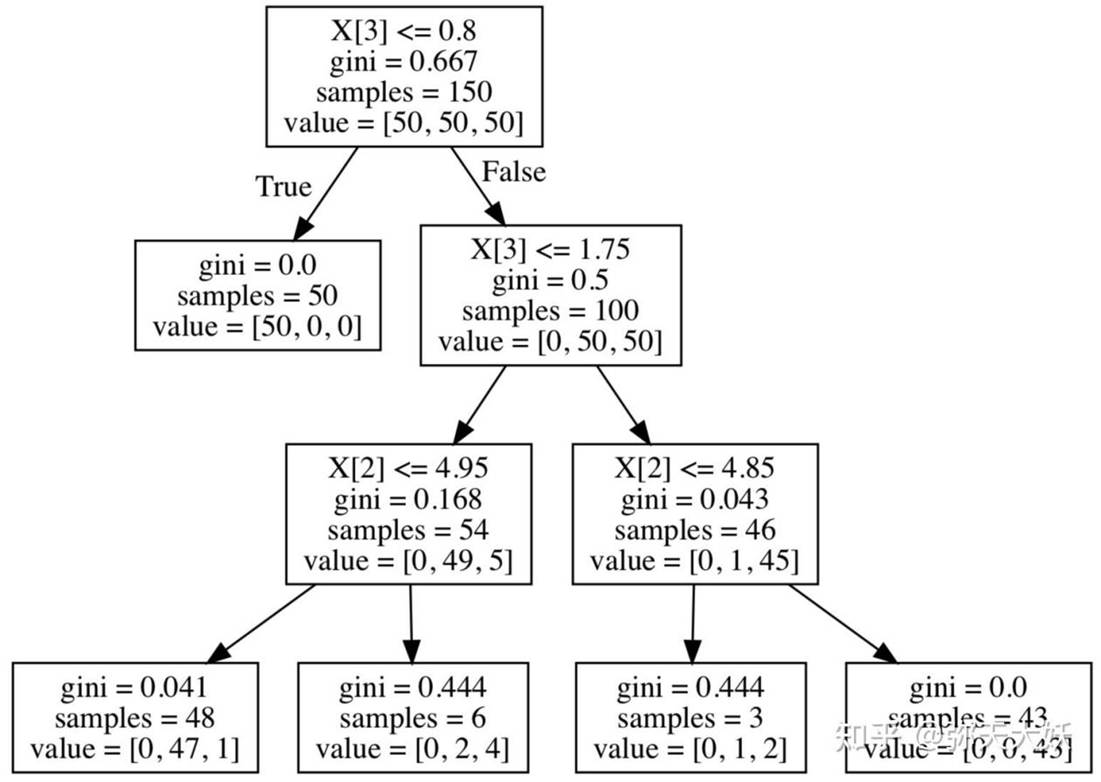
图5 带数据和部分变量的决策树

由于数据表示不当、有噪声或者由于决策树生成时产生重复的子树等原因，都会造成产生的决策树过大。因此，简化决策树是一个不可缺少的环节。寻找一棵最优决策树，主要应解决以下三个最优化问题：生成最少数目的叶子节点；生成的每个叶子节点的深度最小；生成的决策树叶子节点最少且每个叶子节点的深度最小。

CART算法由以下两步组成：决策树生成和决策树剪枝。决策树生成是基于训练数据集生成决策树，生成的决策树要尽量大；决策树剪枝是用验证数据集对已生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准。

图6 CART算法（决策树）

决策树的技术路线

决策树的技术路线主要包括以下几个关键步骤：

1. 特征选择：在决策树学习开始时，如果特征数量很多，需要对特征进行选择，只留下对训练数据有足够分类能力的特征。

图7 特征选择数学表达

2. 决策树的生成：树的生成是通过递归分裂的方式进行的。从根节点开始，使用特征选择方法选择最佳的分裂特征，创建分支，直到满足某个停止条件，比如达到了设定的最大深度，或者节点中的样本数量少于阈值。

3. 决策树的剪枝：为了防止过拟合，即模型对训练数据过于敏感，从而无法泛化到新的数据上，决策树需要进行剪枝。剪枝包括预剪枝和后剪枝。预剪枝是在树完全生成之前停止树的生长；后剪枝则是在树生成之后去掉某些分支。

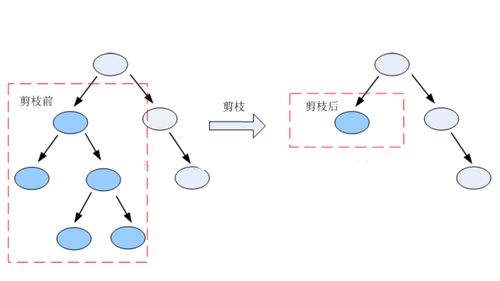
图8 决策树的剪枝

4. 损失函数和策略：决策树学习通常以损失函数最小化为目标函数的最小化，通常是正则化的极大似然函数。（图片详情见图4）

5. 启发式方法：由于从所有可能的决策树中选取最优决策树是NP完全问题，现实中决策树学习通常采用启发式方法，近似求解这一最优化问题，得到的决策树是次最优的。

图9 介绍四种常见的决策树算法

6. 算法实现：决策树学习的算法通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割，使得对各个子数据集有一个最好的分类的过程。

图10 算法实现的一个示例

7. 模型的泛化能力：在选择决策树时，应选择一个与训练数据矛盾较小的决策树，同时具有很好的泛化能力；而且选择的条件概率模型应该不仅对训练数据有很好的拟合，而且对未知数据有很好的预测。

这些步骤共同构成了决策树的技术路线，使得决策树能够从训练数据中学习并构建出能够对新数据进行分类或预测的模型。

问题求解分析和步骤

图11 证券公司员工着装样式

1.问题求解分析

我们可以先行做一个调查，即证券公司会出现什么样的着装组合，那么首先要进行特征的分类，在本例子中分为上衣，下装和鞋子。

然后在收集一些数据，这些数据要从很多个不同的人那里得到，然后分为不同的组，每个组里面有三个数据，每一特征对应一个数据。然后再对这些组别进行人工的判断，即区分出着装规范和不规范两种分类。

2.求解步骤

（1）我们可以看到这样的几个人物着装：

表1 样本空间（输入样例）

这13组数据是实地得到的调研结果，由这些调研结果，我们人工很难迅速的从这些杂乱无章的着装样例中得出在该证券公司怎么穿才是得体的。而这个时候，决策树将开始发挥它的作用。

（2）Claude Shannon 定义了熵（entropy）和信息增益(information gain)。
用熵来表示信息的复杂度，熵越大，则信息越复杂。公式如下：

$H = - \sum_{i=1}^n p(x_i) \log_2 p(x_i)$

由上文中我们对特征值的分类可以知道信息增益是依靠信息熵的大小来确定优先级的，而由公式我们不难看出，信息熵的大小又由占比（P）来决定。因此，特征值的优先级事实上是由其占比来排大哥二哥的。

def calcShannonEnt(dataSet): # 计算数据的熵(entropy)

numEntries=len(dataSet) # 数据条数 labelCounts={}

for featVec in dataSet: #featVec数据集的每一条 currentLabel=featVec[-1] # 每行数据的最后一个字（类别）

if currentLabel not in labelCounts.keys():

labelCounts[currentLabel]=0

labelCounts[currentLabel]+=1 # 统计有多少个类以及每个类的数量 shannonEnt=0

for key in labelCounts:

prob=float(labelCounts[key])/numEntries # 计算单个类的熵值

shannonEnt-=prob*log(prob,2) # 累加每个类的熵值

return shannonEnt

这一串就是计算熵值的函数的代码，体现了这个算法的核心思想。即合理排序。

（3）接下来定义一个函数用来分割数据集，其作用是根据指定的特征（axis）和值（value）对数据集（dataSet）进行分割。具体步骤如下：

初始化一个空列表 retDataSet，用于存储分割后的数据。

遍历数据集中的每个样本 featVec。

对于每个样本 featVec，检查其第 axis 个特征的值是否等于 value。

如果第 axis 个特征的值等于 value，则将该样本的第 axis 个特征之前的所有特征（featVec[:axis]）和第 axis 个特征之后的所有特征（featVec[axis+1:]）拼接起来，形成一个新的特征向量 reducedFeatVec。

将新的特征向量 reducedFeatVec 添加到 retDataSet 中。

重复步骤 3 到步骤 5，直到遍历完数据集中的所有样本。

返回分割后的数据 retDataSet。

这个函数在决策树算法中用于根据某个特征的值对数据集进行划分，以便后续计算信息增益并选择最优的特征进行分类。

（4）接着定义了一个用来确定最优分割位函数，其作用是从数据集中选择最优的特征来进行分类。这个函数是决策树算法中的一个关键步骤，它通过计算每个特征的信息增益来确定哪个特征能够最大程度地减少数据集的不确定性。

函数的工作流程如下：

首先，计算原始数据集的熵（baseEntropy），这是通过调用 calcShannonEnt 函数实现的。熵是衡量数据集混乱程度的指标，熵值越大，数据集的不确定性越高。

然后，遍历数据集中的每个特征（i 从 0 到 numFeatures-1），对于每个特征，执行以下操作：

创建一个列表 featList，包含数据集中所有样本的第 i 个特征的值。

使用 set 函数创建一个集合 uniqueVals，包含 featList 中的所有唯一值。

初始化一个变量 newEntropy 为 0，用于存储按当前特征划分后的熵。

遍历 uniqueVals 中的每个值 value，对于每个值，执行以下操作：

使用 splitDataSet 函数根据当前特征和值 value 对数据集进行分割，得到一个子集 subDataSet。

计算子集 subDataSet 的概率 prob，即 subDataSet 中的样本数除以原始数据集的样本数。

将 prob 乘以 subDataSet 的熵 calcShannonEnt(subDataSet)，并累加到 newEntropy 中。

计算当前特征的信息增益 infoGain，即原始熵 baseEntropy 减去按当前特征划分后的熵 newEntropy。

如果当前特征的信息增益 infoGain 大于之前记录的最大信息增益 bestInfoGain，则更新 bestInfoGain 和 bestFeature，记录当前特征为最优特征。

遍历所有特征后，返回具有最大信息增益的特征索引 bestFeature。

这个函数的目的是找到能够最大程度减少数据集不确定性的特征，从而帮助构建决策树。通过选择最优特征进行分裂，可以使得决策树的每个分支都包含尽可能纯净的数据集，提高分类的准确性。

（5）再接着定义一个用来找最大类别的函数，其作用是在给定的类别列表 classList 中，找出出现次数最多的类别，并返回该类别。这个函数通常用于决策树算法中的叶子节点，当所有的数据样本都属于同一类别时，决策树就会停止分裂，选择这个多数类作为预测结果。

函数的工作流程如下：

首先，创建一个空字典 classCount，用于存储每个类别的出现次数。

然后，遍历类别列表 classList 中的每个元素 vote。

对于每个元素 vote，检查它是否已经在 classCount 字典的键中。如果不在，就将其添加到字典中，并设置其出现次数为 0。

如果元素 vote 已经在字典中，就将其出现次数加 1。

遍历完成后，使用 Python 的 sorted 函数对 classCount 字典的键值对进行排序。排序的依据是每个类别的出现次数，即字典的值。排序方式是降序，即出现次数最多的类别排在最前面

sorted 函数返回一个列表，其中每个元素是一个元组，包含字典的键和值。我们只对第一个元组感兴趣，因为它对应出现次数最多的类别。

最后，返回排序后的列表中第一个元组的第一个元素，即出现次数最多的类别。

这个函数的目的是在决策树的构建过程中，当无法继续分裂时，选择一个最有可能的类别作为预测结果。通过统计每个类别的出现次数，并选择出现次数最多的类别，可以提高决策树的预测准确性。

（6）最后定义一个名为创建树的函数，它是构建决策树的核心部分。这个函数通过递归的方式，根据数据集和特征标签来构建决策树。

函数的工作流程如下：

首先，函数从数据集中提取所有样本的类别标签，存储在 classList 中。

然后，函数检查 classList 中是否所有的类别标签都相同。如果是，说明数据集已经是纯净的，即所有样本都属于同一类别。此时，函数直接返回这个类别作为决策树的叶子节点。

如果 classList 中的类别标签不相同，函数检查数据集的特征数量是否为 1。如果是，说明已经没有更多的特征可以用来划分数据集，此时函数调用 majorityCnt 函数来确定多数类，并将其作为决策树的叶子节点。

如果数据集的特征数量大于 1，函数调用 chooseBestFeatureToSplit 函数来选择最优的特征进行划分。这个函数通过计算信息增益来确定哪个特征能够最大程度地减少数据集的不确定性。

选择了最优特征后，函数将这个特征的标签存储在 bestFeatLabel 中，并创建一个以 bestFeatLabel 为键的字典 myTree，用于存储决策树的节点。

接下来，函数从原始的特征标签列表 labels 中删除已经选择的最优特征，因为这个特征已经被用来划分数据集，不再需要参与后续的划分。

然后，函数遍历最优特征的所有可能取值 uniqueVals，对于每个取值，它创建一个新的子数据集 subDataSet，其中只包含该取值对应的样本。

对于每个子数据集，函数创建一个新的子树，并将其作为 myTree 中对应特征取值的子节点。这个子树是通过递归调用 createTree 函数来构建的，传入的参数是子数据集和更新后的特征标签列表 subLabels。

最后，函数返回构建好的决策树 myTree。

这个函数通过不断选择最优特征并划分数据集，构建出一个树形结构，其中每个内部节点代表一个特征的划分，每个叶子节点代表一个类别。这样，当新的数据样本到达时，我们可以根据决策树的结构来预测它的类别。

输入层:

以上的各大函数均体现算法的内核，其是对各种功能的合适封装，主函数部分只需要一个print和一个输入处理层就行了，那么问题是输入处理还要有很长一段的代码实现，因此还得进行封装。

为了实现强移植性和可交互性，我加入了很多的input环节，不过需要使用者明确什么是特征，什么是样本数据，以及样本数据怎么输入的问题（当然了，这其实CTRL+c excel表格，接着CTRL+V 到cmd就行了）。接下来看看我们需要输入什么：

我们总共需要输入一个dataset表格和一个label表格，其中label要求是字符串组成的列表，这与dataset的要求不同，很容易出bug这里，还是要小心。在输入时要先输入目标表格内元素的数量，还有特征值的数量，然后在输入的时候要注意split()这个条件，其他的也没什么，这个程序的输入层就完成了。

总结：这个程序有种简化交互，深藏功与名的感觉，因为你看整个实现过程，函数的代码量以及复杂程度是远远大于主函数的，而且合适的函数封装使得主函数界面非常简洁，同行一看就知道这个程序主要在干什么，其次，丰富的注释更是加强了代码阅读者的理解，不得不称赞是个不错的工程。

程序代码

from math import *
import operator

def calcShannonEnt(dataSet):  # 计算数据的熵(entropy)
    numEntries=len(dataSet)  # 数据条数   numEntries=8 条记录
    labelCounts={}
    for featVec in dataSet:   #featVec数据集的每一条
        currentLabel=featVec[-1] # 每行数据的最后一个字（类别）
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel]=0
        labelCounts[currentLabel]+=1  # 统计有多少个类以及每个类的数量
    shannonEnt=0
    for key in labelCounts:
        prob=float(labelCounts[key])/numEntries # 计算单个类的熵值
        shannonEnt-=prob*log(prob,2) # 累加每个类的熵值
    return shannonEnt

def createDataSet():    # 创造示例数据
    dataSet = []
    i=0
    j=0
    sample_number=0
    label_number=0
    print("请输入特征数量：")
    label_number=int(input())
    print("请输入样例数量：")
    sample_number=int(input())
    print("请输入样例数据：")
    for i in range(sample_number):
        dataSet.append(list(input().split()))
    labels = []  #两个特征
    print("请输入特征名称：")
    for j in range(label_number):
        label = input().strip()  # 获取输入并去除前后空格
        labels.append(label)  # 直接添加字符串到labels列表
    return dataSet,labels

def splitDataSet(dataSet,axis,value): # 按某个特征分类后的数据
    retDataSet=[]
    for featVec in dataSet:
        if featVec[axis]==value:
            reducedFeatVec =featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

def chooseBestFeatureToSplit(dataSet):  # 选择最优的分类特征
    numFeatures = len(dataSet[0])-1  #numFeatures取值排除分类结果项
    baseEntropy = calcShannonEnt(dataSet)  # 原始的熵
    bestInfoGain = 0
    bestFeature = -1
    for i in range(numFeatures):  #i取值0和1
        featList = [example[i] for example in dataSet] #featList为数组，取值为单特征记录
        uniqueVals = set(featList)  #构建无重复记录的单特征数组uniqueVals
        newEntropy = 0
        for value in uniqueVals:  #遍历特征的各个不重复记录
            subDataSet = splitDataSet(dataSet,i,value)
            prob =len(subDataSet)/float(len(dataSet))
            newEntropy +=prob*calcShannonEnt(subDataSet)  # 按特征分类后的熵
        infoGain = baseEntropy - newEntropy  # 原始熵与按特征分类后的熵的差值
        if (infoGain>bestInfoGain):   # 若按某特征划分后，熵值减少的最大，则次特征为最优分类特征
            bestInfoGain=infoGain
            bestFeature = i
    return bestFeature

def majorityCnt(classList):    #按分类后类别数量排序，比如：最后分类为2着装得体1不得体，则判定为着装得体；
    classCount={}    #classCount定义字典变量,形式为{'':','':}
    #print(classList)
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote]=0
        classCount[vote]+=1
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    #classCount.items为字典键值，operator.itemgetter(1)获取对象classCount第2个域，True由大到小
    #sorted区别于sort，不改变原classCount的内容    
    return sortedClassCount[0][0]   #返回类别'男'

def createTree(dataSet,labels):
    classList=[example[-1] for example in dataSet]  # 类别：男或女 ;类别记录数组
    #print(classList)
    if classList.count(classList[0])==len(classList): #classList.count(classList[0])统计"男"个数
        return classList[0]
    #print(dataSet[0])
    #print(len(dataSet[0]))
if len(dataSet[0])==1:  
len(dataSet[0])=3
        return majorityCnt(classList)    #如果满足==1条件即为同一类，则按类别由大到小排序
    bestFeat=chooseBestFeatureToSplit(dataSet) #选择最优特征
    bestFeatLabel = labels[bestFeat]
    myTree={bestFeatLabel:{}} #分类结果以字典形式保存

    del(labels[bestFeat])
    featValues=[example[bestFeat] for example in dataSet]
    uniqueVals=set(featValues)
    for value in uniqueVals:
        subLabels=labels[:]
        myTree[bestFeatLabel][value]=createTree(splitDataSet\
                            (dataSet,bestFeat,value),subLabels)
    return myTree


if __name__=='__main__':
    dataSet, labels=createDataSet()  # 创造示列数据
print(createTree(dataSet, labels))  # 输出决策树模型结果

运行结果

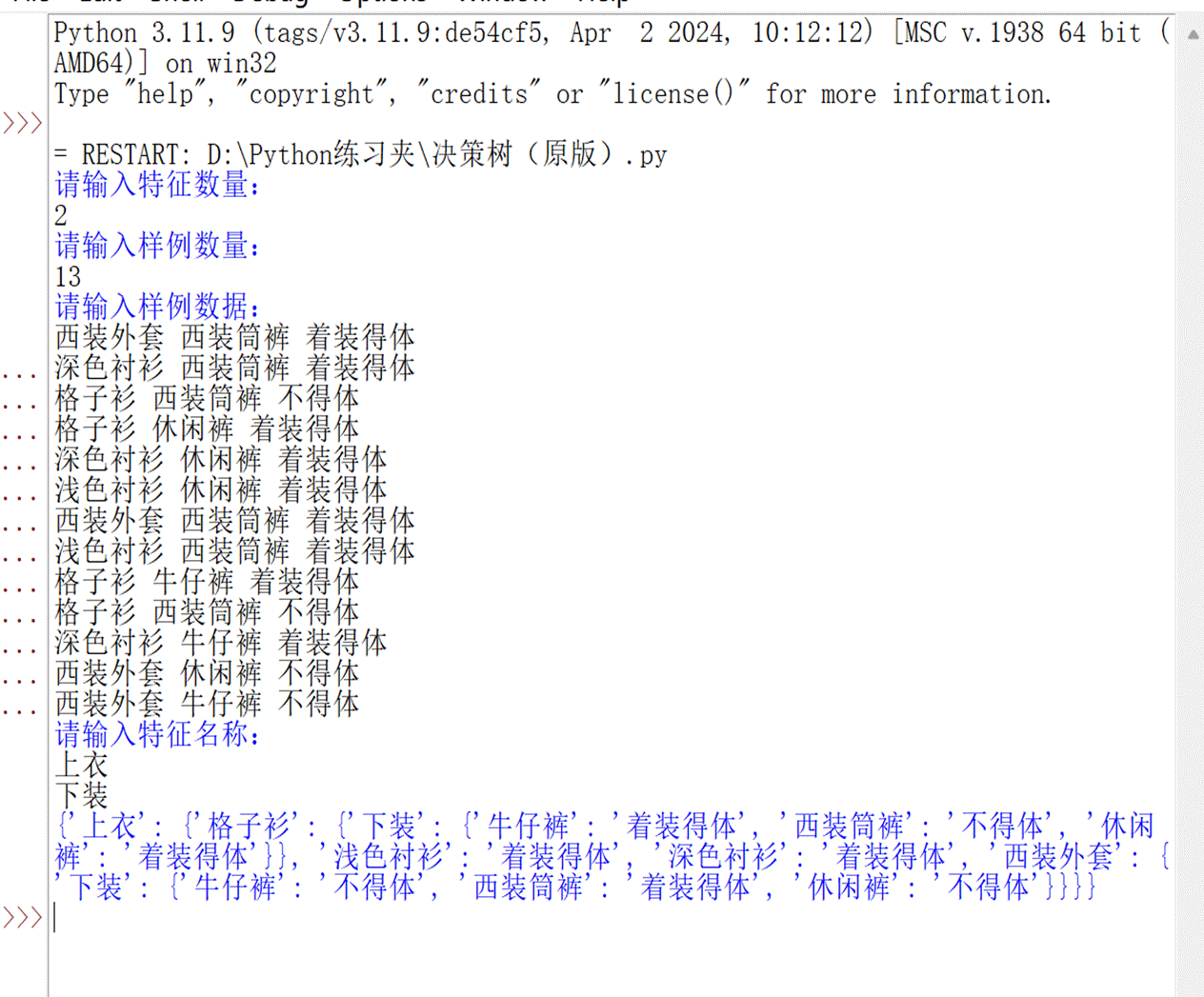
图12 决策树运行结果

这个结果其实就是一个决策树，不过这个不直观，我下面画一个正规一点的，可以被更多人接受的决策“树”。

决策树（即流程图）

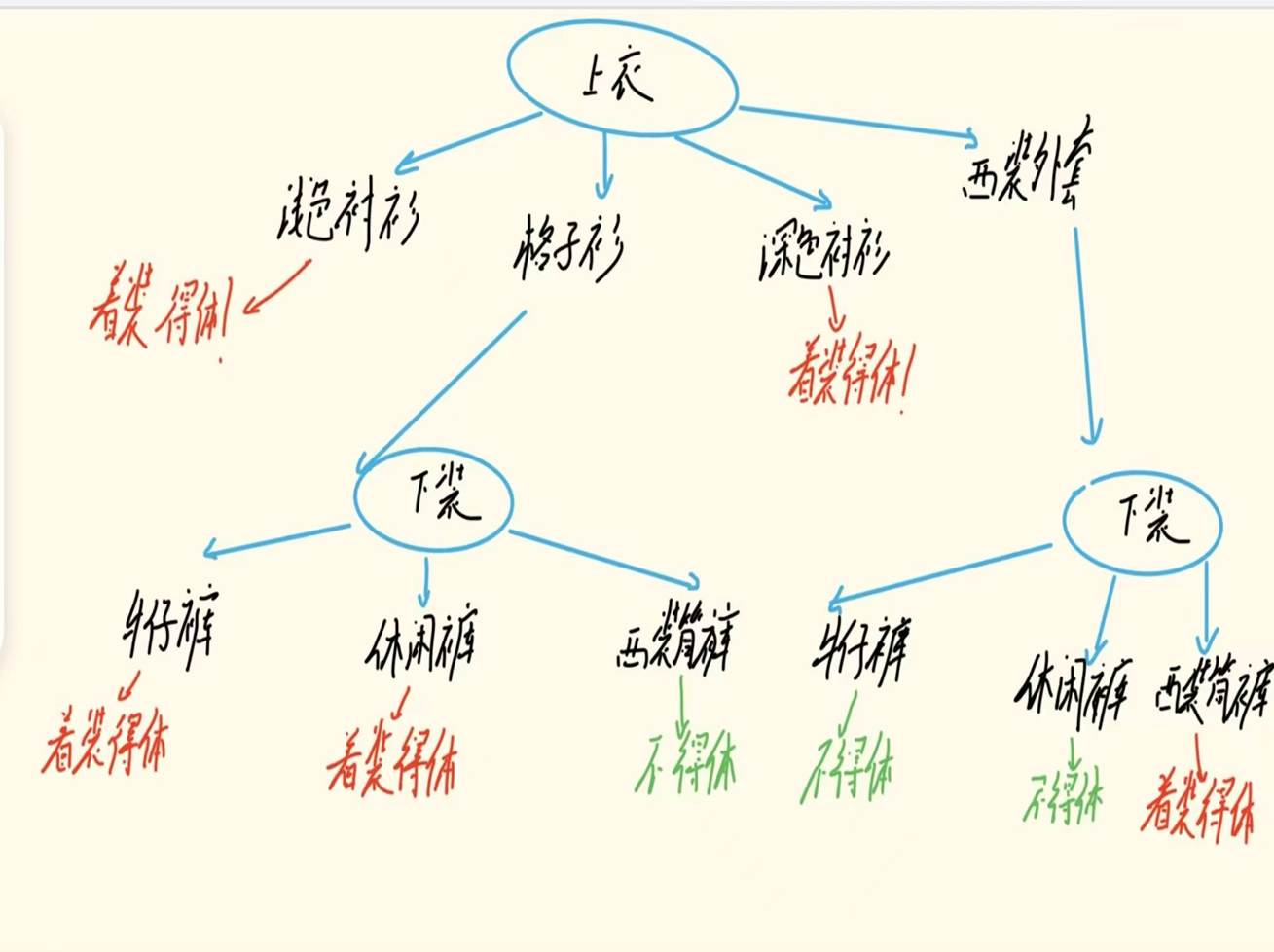
图13 手绘的决策树

这个决策树呈现了一个从起始节点（起点）出发，通过一系列选择逐步达到不同结果的决策过程。首先，在第一个决策节点（决策1），需要做出第一个选择，这个选择将引导我们进入不同的分支。接着，在第二个决策节点（决策2），根据前一个选择的结果，继续做出第二个选择，以此类推。

在决策过程中，每个分支都代表了一个可能的选择路径，而每个路径上的节点则代表了不同的决策点或状态。这些节点不仅帮助我们跟踪决策的进程，还提供了关于每个决策点的详细信息。

最终，经过一系列的决策和选择，每个路径都会导向一个特定的结果节点（结果1、结果2等），这些结果节点在决策树的末端被明确标出。通过这种方式，决策树提供了一个清晰的视觉化表示，帮助我们理解和分析复杂决策过程中的各种可能性和结果。

五.个人心得

决策树学习作为一种直观且强大的机器学习方法，给我留下了深刻的印象。它不仅易于理解和解释，而且在处理分类和回归问题时表现出色。通过构建决策树，我们可以将复杂的数据集分解为更简单的决策规则，这些规则有助于揭示数据背后的模式和趋势。

在学习决策树的过程中，我深刻体会到数据预处理的重要性。决策树的构建依赖于输入数据的质量，因此数据清洗和特征选择成为成功应用决策树的关键步骤。通过去除噪声和不相关的特征，我们可以提高模型的准确性和泛化能力。此外，特征的编码方式也会影响决策树的构建，因此对分类特征进行适当的编码是必不可少的。

决策树的一个显著优点是其模型的透明性。与其他黑箱模型不同，决策树允许我们直观地看到每个决策节点和分支，这使得模型的解释变得简单。这种透明性不仅有助于我们理解模型是如何做出预测的，而且也使得向非技术利益相关者解释模型变得更加容易。然而，这种透明性也带来了一些挑战，尤其是在处理具有大量特征和类别值的数据集时，决策树可能会变得非常复杂和难以管理。

在实际应用中，我意识到过拟合是决策树学习中一个常见的问题。由于决策树可以无限地分割数据，直到每个叶节点只包含一个类别的样本，这可能导致模型在训练数据上表现得非常好，但在未见过的数据上表现不佳。为了避免过拟合，我们需要采取一些措施，如剪枝、设置树的最大深度或最小样本分割数。这些技术有助于简化模型，提高其在新数据上的泛化能力。

此外，我还了解到决策树的集成方法，如随机森林和梯度提升树，可以显著提高模型的性能。这些集成方法通过构建多个决策树并结合它们的预测结果来减少过拟合的风险，并提高模型的稳定性和准确性。通过学习这些高级技术，我认识到决策树不仅可以单独使用，还可以与其他模型结合使用，以解决更复杂的机器学习问题。

在实践中，我还发现特征的重要性评估是决策树学习中的一个重要方面。通过分析决策树中的特征分裂点，我们可以了解哪些特征对模型的预测能力贡献最大。这种特征重要性评估不仅有助于我们理解数据集的关键驱动因素，而且还可以指导我们在未来的数据收集和特征工程中做出更明智的决策。

在深入学习决策树算法的过程中，我对Python中的数据结构有了更深刻的理解和掌握。Python的列表、元组、集合等数据结构与C语言中的数组、结构体等有着本质的不同，它们的灵活性和内置功能大大简化了数据处理的复杂性，但同时也要求我们对它们的特性有更深入的了解。

图14 用VScode修改和编写程序的插图

列表（List）是Python中最常用的数据结构之一，它是一个有序的元素集合，可以包含不同类型的数据。列表的动态特性使得在决策树算法中处理数据集变得非常方便。例如，在构建决策树时，我们可以轻松地添加、删除或修改列表中的元素，以适应不同的数据处理需求。然而，列表的这种灵活性也意味着我们需要更加注意数据的一致性和类型匹配，以避免在运行时出现错误。

元组（Tuple）与列表类似，但它是不可变的。这意味着一旦元组被创建，它的元素就不能被修改。在决策树算法中，元组常用于存储不应该改变的数据记录，如特征名称或类别标签。使用元组可以确保数据的完整性，防止在算法执行过程中被意外修改。然而，元组的不可变性也要求我们在设计算法时更加谨慎，确保数据的正确性和一致性。

集合（Set）是一个无序且不重复的元素集合，它在处理特征选择和类别标签时非常有用。集合的特性使得它在执行集合操作（如并集、交集、差集）时非常高效。在决策树算法中，我们可以利用集合来快速识别和处理特征的唯一值，从而优化特征分裂的选择。然而，集合的无序性也意味着我们不能依赖元素的顺序，这在某些特定的数据处理场景中可能会带来挑战。

在学习和实践决策树算法的过程中，我还体会到了Python中数据结构的嵌套使用。例如，我们可以将列表嵌套在列表中，或将元组嵌套在字典中，以构建复杂的数据结构来表示决策树。这种嵌套使用不仅提高了数据表示的灵活性，也要求我们更加注意数据结构的设计和管理，以确保算法的正确性和效率。

通过对Python数据结构的深入学习，我认识到在决策树算法中，选择合适的数据结构对于算法的性能和稳定性至关重要。每种数据结构都有其特定的用途和限制，正确地使用它们可以显著提高算法的效率和准确性。同时，我也意识到在实际编程中，对数据结构的不当处理可能会导致各种BUG，因此在编写代码时需要更加细心和严谨。通过这次学习，我不仅提高了自己的编程技能，也加深了对数据结构和算法之间关系的理解。

图15 一个漂亮的决策树

通过这次宝贵的项目经历，我得以更加深入地学习和理解了计算机智能技术领域内，特别是人工智能（AI）中的决策树算法。在这个过程中，我不仅掌握了理论知识，还通过实践操作，解决了自己之前在学习过程中积累的许多疑惑和问题。在项目开始之前，我更多地是作为一个修复程序中各种bug的专家，而通过这次实践，我深刻体会到了“旧病成医”这句老话在我身上的体现。我从一个简单的bug修复者，逐渐成长为能够理解和运用复杂算法的开发者。

图16 最后附上debugging的截图