题解：[CSP-J2019 江西] 道路拆除

题解：[CSP-J2019 江西] 道路拆除

题意：

求总路径数量-A国首都(即点1)到$s_1$和$s_2$的综合最短路的答案

思路：

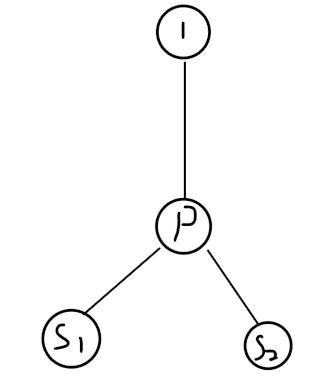
如果要求A国首都(即点1)到$s_1$和$s_2$的综合最短路，那么答案一定呈一个$Y$字型(如下图)

读图可知：$1-p$的距离每多1，$s_1$到$p$加$s_2$到$p$的距离就少1。

这时就可以让$1-p$的距离尽可能大，可以想到枚举$p$点，时间复杂度：$O(N)$。

可以考虑分别从点$1$,$s_1$,$s_2$三点分别做一次$BFS$，最后遍历$p$点找到最优解。

$code:$(不喜勿喷)

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define itn int
#define N 3100
#define MAX 100000000
int n,m,s1,s2,t1,t2;
vector<int>a[N];//存图
vector<int>book1(N,MAX);//记录1为起点的答案
vector<int>books1(N,MAX);//记录s1为起点的答案
vector<int>books2(N,MAX);//记录s2为起点的答案
int vis[N];//记录是否走过
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int u,v;
        cin>>u>>v;
        a[u].push_back(v);
        a[v].push_back(u);
    }
    cin>>s1>>t1>>s2>>t2;
    queue<int>q;
    q.push(1);//不要忘记初始化！！！
    vis[1]=1;
    book1[1]=0;
    //第一遍BFS
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int v:a[u]){
            if(!vis[v]){
                vis[v]=1;
                q.push(v);
                book1[v]=book1[u]+1;
            }
        }
    }
    memset(vis,0,sizeof vis);//清空！！！
    q.push(s1);
    vis[s1]=1;
    books1[s1]=0;
    //第二遍
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int v:a[u]){
            if(!vis[v]){
                vis[v]=1;
                q.push(v);
                books1[v]=books1[u]+1;
            }
        }
    }
    memset(vis,0,sizeof vis);//清空
    q.push(s2);
    books2[s2]=0;
    vis[s2]=1;
    //第三遍
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int v:a[u]){
            if(!vis[v]){
                vis[v]=1;
                q.push(v);
                books2[v]=books2[u]+1;
            }
        }
    }
    int mins=MAX;
    for(int i=1;i<=n;i++){
        int anss=book1[i]+books1[i]+books2[i];
        //符合时间才计算
        if(book1[i]+books1[i]<=t1&&book1[i]+books2[i]<=t2)mins=min(mins,anss);
    }
    if(mins>=MAX){//不要忘记-1
        cout<<-1;
        return 0;
    }
    cout<<m-mins;
    return 不要直接复制！！！;
}