Matlab在频域分析中的基础应用

概述

频域分析的原理是线性系统在受到正弦信号输入时，其输出的幅值和相位随着输入信号的频率变化而变化。

本文介绍用Matlab绘制奈奎斯特图和伯德图的方法并总结伯德图判读的相关知识

Matlab版本为2022b，文中所有代码都可以直接运行

---

奈奎斯特图

已知系统开环传递函数如图

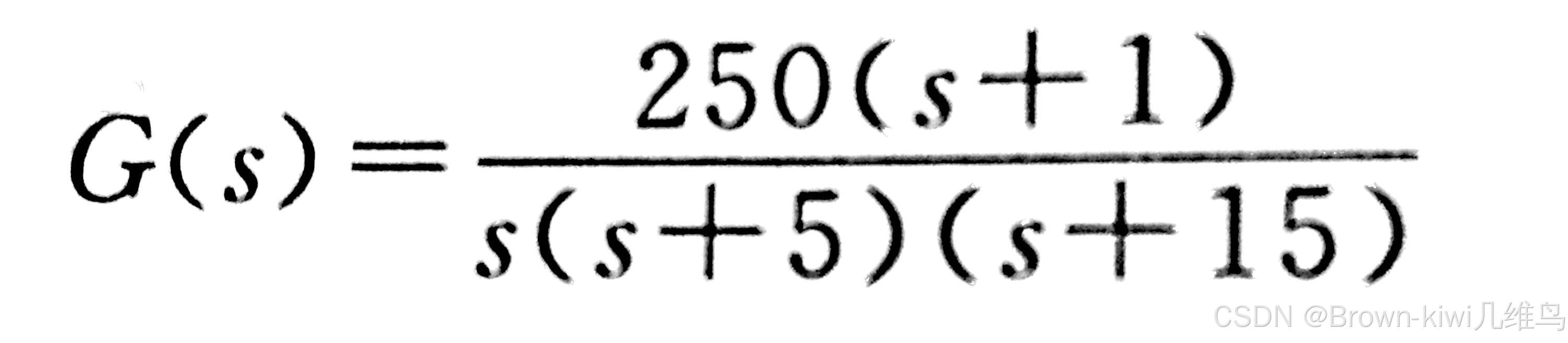
绘制奈奎斯特图的代码如下

num=[250,250];%定义传递函数的分子矢量
den=conv([1,0],conv([1,5],[1,15]));%定义传递函数分母矢量，conv是卷积
sys=tf(num,den);%建立传递函数
nyquist(sys)%画奈奎斯特图

图像如下

图像没有包围（-1,0j）点，所以系统稳定

---

伯德图

已知开环传递函数如下

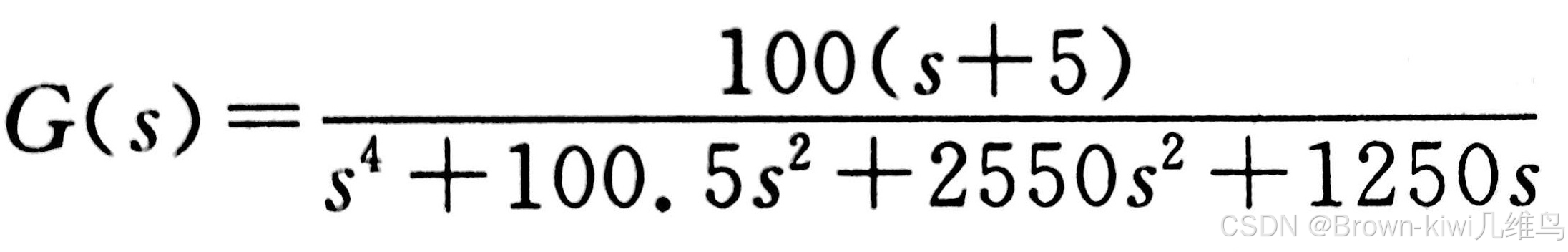
代码如下

num=[100,500];%分子矢量
den=[1,100.5,2550,1250,0];%分母矢量
sys=tf(num,den);%建立传递函数
margin(sys);%绘制伯德图并标出稳定裕量
grid on%给图像增加网格
[Gm,Pm,Wcg,Wcp]=margin(sys)%输出Gm增益裕量,Pm相位裕量,Wcg相位穿越频率,Wcp增益穿越频率

伯德图如下

相关输出值如下

---

伯德图判读

低频段	斜率中等比较好 斜率越大则稳态误差越小 斜率太大则系统不稳定
中频段	斜率偏小比较好 相位裕量在30°-60°之间则系统稳定性好，同时时域上的超调量σ适中 幅值穿越频率wc越大，系统快速性越好
高频段	斜率大比较好 衰减的越快越好