【数据结构入门】2.1.1+2线性表（持续更新ing）（线性表的定义、特点）

线性表（持续更新ing）（线性表的定义、特点）

数据结构 手写笔记+思维导图资源，希望大家支持哈哈
建议大家下点赞收藏 pc端下载思维导图哦 看的清晰一点，内容更详细
配套学习的 数据结构与算法基础（青岛大学-王卓）老师 的课程
可以配合课程一起学习哈 （章节思维导图是同步的，文章内图片也有部分截取）

目录

• 线性表定义和特点
• 线性表逻辑特征
• 线性表典型案例引入
• 线性表存储结构
  • 顺序存储结构
  • 链式存储结构
  • 案例应用2：图书信息管理系统
• 抽象数据类型思想

线性表定义和特点

线性表是具有相同性质的数据元素的一个有限序列

• 线性表 (Linear List)
  由 n (n≥0) 个数据元素 (结点) a₁，a₂，…aₙ组成的有限序列
  数据元素个数 n 为表的长度
  n = 0 时为空表
  非空线性表 (n>0) 记作：(a₁，a₂，…aₙ)
  数据元素 aᵢ(1≤i≤n) 是抽象符号，具体含义依情况而定
• 示例
  • 26个英文字母序列：( (A, B, C… Z) )
  • 某单位历年计算机数量：( (6, 17, 28, 50, 92, 188) )
  • 12星座序列：(白羊座、金牛座、双子座、…、双鱼座)
    同一线性表中的元素必定具有相同特性，数据元素间的关系是线性关系

线性表逻辑特征

1. 开始结点：仅有一个开始结点 a1 ，无直接前驱，仅有直接后继 a2
2. 终端结点：仅有一个终端结点 an，无直接后继，仅有直接前趋 an-1
3. 内部结点：其余内部结点 ai（2 小于等于 i 小于等于 n - 1），都有且仅有一个直接前趋 ai-1 和一个直接后继 ai+1

• 性质：线性表是一种典型的线性结构

线性表典型案例引入

案例2.1.1：一元多项式运算

一元多项式的运算：实现两个多项式加、减、乘运算

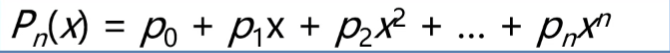
案例2.1.2：稀疏多项式运算

如果这种按照上面的方法来实现会非常浪费空间
多项式非零项的数组表示

• 案例(a)：

• 案例(b)：按以上方式可以ab可以表达成
  -线性表 A = ((7, 0), (3, 1), (9, 8), (5, 17))
  -线性表 B = ((8, 1), (22, 7), (-9, 8))

• 运算逻辑

  1. 创建新数组 ( C )
  2. 从头遍历比较 ( A ) 和 ( B ) 的每一项
     • 指数相同：系数相加，和不为零则在 ( C ) 中新增项
     • 指数不同：复制指数较小的项到 ( C )
  3. 遍历完毕后复制剩余项到 ( C )

线性表存储结构

顺序存储结构

• 问题
  1. 存储空间分配不灵活（可能造成空间浪费）
  2. 插入/删除需移动大量元素，效率低

链式存储结构

案例应用1：任然使用上面提到的AB

4.这里系数相同相加为0就不计入了，同时b中没有数据了转到a

案例应用2：图书信息管理系统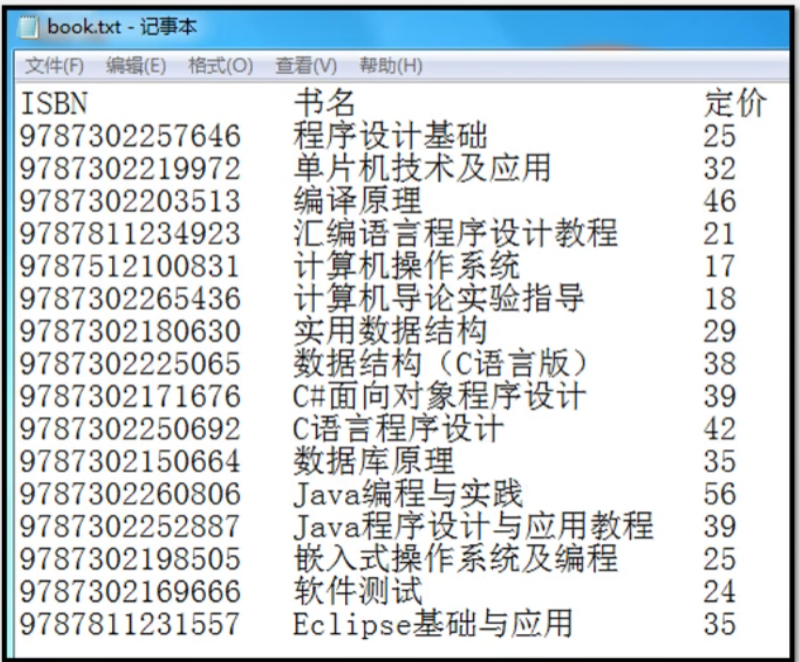需要的功能：

(1) 查找 (2) 插入
(3) 删除 (4) 修改
(5) 排序 (6) 计数

• 抽象模型
  • 图书表 → 线性表
  • 每本图书 → 线性表中的数据元素
• 存储结构

  • 顺序结构：连续存储

  • 链式结构：非连续存储

抽象数据类型思想

1. 数据元素类型：可支持简单类型或复杂类型
2. 核心思想
   • 许多实际应用问题所涉的基本操作有很大相似性，不应为每个具体应用单独编写一个程序
   • 从具体应用中抽象出共性的逻辑结构和基本操作（抽象数据类型），然后实现其存储结构和基本操作

最后老样子我附上全文的思维导图预览，大家需要的话可以在电脑端下载完整思维导图哦，看的更加清楚

如果文章对您有启发，欢迎点赞、收藏、评论，您的支持是我持续创作的最大动力～
如果文中存在疏漏，欢迎在评论区留言，我会尽力完善～
感谢每一位读者的阅读与陪伴，咱们下期再见！ 😊