2.4 线性表的顺序表示和实现
数据结构 手写笔记+思维导图资源,希望大家支持哈哈
建议大家下点赞收藏 pc端下载思维导图哦 看的清晰一点,内容更详细
配套学习的 数据结构与算法基础(青岛大学-王卓)老师 的课程
可以配合课程一起学习哈 (章节思维导图是同步的,文章内图片也有部分截取)
目录
线性表的顺序存储表示
线性表的顺序表又称为顺序存储结构或顺序映像
顺序存储的定义
是把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。
线性表的第一个数据元素a1的存储位子,称作线性表的起始位置或基地址。
顺序存储结构优点:
-
结构简单,存储密度大。
-
线形表顺序存储结构占用一片连续的存储空间。
-
知道某个元素的存储位置就可以计算其他元素的存储位置
逻辑结构与物理结构一致:
a 1 , a 2 , … , a i , … , a n ⇒ L O C ( a 1 ) , L O C ( a 2 ) , … , L O C ( a i ) , … , L O C ( a n ) a_1, a_2, \dots, a_i, \dots, a_n \quad \Rightarrow \quad LOC(a_1), LOC(a_2), \dots, LOC(a_i), \dots, LOC(a_n) a1,a2,…,ai,…,an⇒LOC(a1),LOC(a2),…,LOC(ai),…,LOC(an)

线性表的顺序存储位置计算公式
存储位置公式:
设线性表从数组 elem[0] 开始存储,元素类型大小为 k 字节,则第 ( i ) 个元素的地址为:
L O C ( a i ) = L O C ( a 1 ) + ( i − 1 ) × k LOC(a_i) = LOC(a_1) + (i - 1) \times k LOC(ai)=LOC(a1)+(i−1)×k
例子:
LOC(a_1) = 1000,k = 4,i = 6:
LOC(a_6) = 1000 + (6 - 1) × 4 = 1020

线性表的结构表示
顺序表结构体定义如下:
线性表可变(删除)(数组长度不可动态定义)
用一变量表示顺序表的长度属性
顺序表结构体定义如下:
#define MAXSIZE 100
typedef struct {
ElemType elem[MAXSIZE]; // 数据元素
int length; // 当前长度
} SqList;
优点:
- 存储密度大(除少量附加信息外,无额外指针)。
- 支持随机访问(通过下标)。
- 以物理位置相邻表示逻辑关系。任一元素均可随机存取。
缺点:
- 插入/删除操作需要移动元素
- 空间不易扩展,容易溢出或浪费。
- 容量固定,需预设。
多项式的顺序存储表示定义
用结构体数组表示多项式各项。
#define MAXSIZE 1000 // 多项式项数上限
typedef struct {
int coef; // 系数
int expn; // 指数
} Polynomial; // 单项式类型
typedef struct {
Polynomial elem[MAXSIZE]; // 多项式所有项
int length; // 当前项数
} SqList; // 多项式顺序表结构
这里polynomial是结构体数组,下面是指向结构体的指针和嵌套结构体的结构体
多项式表示示例
多项式表达:
P ( x ) = p 1 x e 1 + p 2 x e 2 + ⋯ + p m x e m P(x) = p_1 x^{e_1} + p_2 x^{e_2} + \dots + p_m x^{e_m} P(x)=p1xe1+p2xe2+⋯+pmxem
对应顺序表存储为:
(p1, e1), (p2, e2), ..., (pm, em)

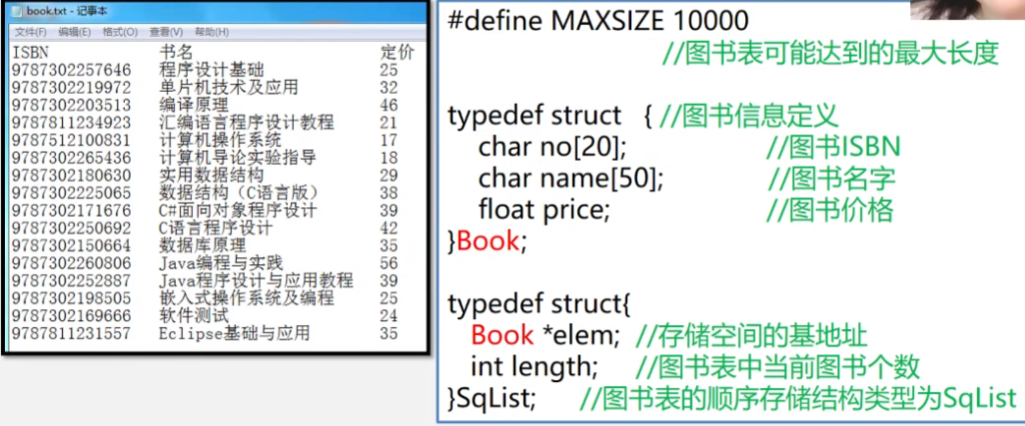
举例:图书表的顺序存储结构类型定义
最后老样子我附上全文的思维导图预览,大家需要的话可以在电脑端下载完整思维导图哦,看的更加清楚

如果文章对您有启发,欢迎点赞、收藏、评论,您的支持是我持续创作的最大动力~
如果文中存在疏漏,欢迎在评论区留言,我会尽力完善~
感谢每一位读者的阅读与陪伴,咱们下期再见! 😊

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








