题目:http://codeforces.com/contest/392/problem/C
题意:给定Fibonacci数列F[],令

分析:对于Fibonacci数列的题目来说一般要构造矩阵。那么本题应该怎样解决?
首先我们设
因为
所以得到
那么,我们继续有
然后我们可以构造矩阵了。。。如下
到了这里,本题完美解决!!!
代码:
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef long long LL;
const int N = 105;
const int M = 45;
const LL MOD = 1000000007;
LL C[M][M];
struct Matrix
{
LL m[N][N];
};
Matrix A,I;
void Init()
{
for(int i=0;i<M;i++)
{
C[i][0] = C[i][i] = 1;
if(i == 0) continue;
for(int j=1;j<=i;j++)
C[i][j] = (C[i-1][j] % MOD + C[i-1][j-1] % MOD) % MOD;
}
}
void InitMatrix(int k)
{
int n = 2 * k + 3;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
I.m[i][j] = (i == j);
}
A.m[0][0] = 1;
for(int i=1;i<n;i++)
{
if(i <= k + 1)
A.m[0][i] = C[k][k+1-i];
else
A.m[0][i] = A.m[0][i-k-1];
}
for(int i=1;i<n;i++)
A.m[i][0] = 0;
for(int i=1;i<n;i++)
{
if(i <= k + 1)
{
for(int j=1;j<n;j++)
{
if(j < i) A.m[i][j] = 0;
else
{
if(j <= k + 1)
A.m[i][j] = C[k+1-i][k+1-j];
else
A.m[i][j] = A.m[i][j-k-1];
}
}
}
else
{
for(int j=1;j<n;j++)
{
if(j < i - k - 1) A.m[i][j] = 0;
else
{
if(j <= k + 1)
A.m[i][j] = A.m[i-k-1][j];
else
A.m[i][j] = 0;
}
}
}
}
}
Matrix multi(Matrix a,Matrix b,int n)
{
Matrix c;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
c.m[i][j] = 0;
for(int k=0;k<n;k++)
{
c.m[i][j] += a.m[i][k] * b.m[k][j] % MOD;
c.m[i][j] %= MOD;
}
}
}
return c;
}
Matrix power(Matrix A,int n,LL k)
{
Matrix ans = I, p = A;
while(k)
{
if(k & 1 )
{
ans = multi(ans,p,n);
k--;
}
k >>= 1;
p = multi(p,p,n);
}
return ans;
}
int main()
{
Init();
LL n;
int k;
while(cin>>n>>k)
{
InitMatrix(k);
Matrix t = power(A,2*k+3,n-1);
LL ans =0;
for(int i=0;i<2*k+3;i++)
{
ans += t.m[0][i];
ans %= MOD;
}
cout<<ans<<endl;
}
return 0;
}








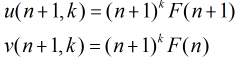
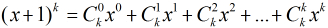
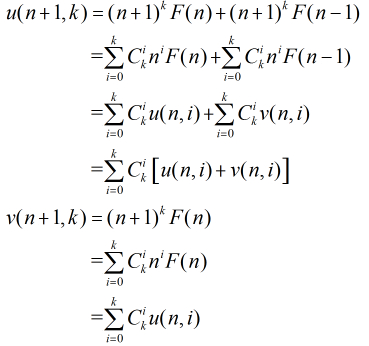
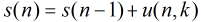















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








