今天,我要介绍我们早就知道的一种分布,它叫做高斯分布。高斯分布在概率论中算是比较核心的一种分布了,而在机器学习中,高斯分布也随处可见,比如单高斯模型,高斯混合模型,高斯过程等等,它们都是基于高斯分布的。作为理解连续性随机变量的基础和深入理解在机器学习中的广泛应用,高斯分布是十分有必要学习的。
高斯分布又叫做正态分布,高斯分布概率密度函数的函数形式是由德国著名的天才数学家、统计学家、物理学家和天文学家高斯推导出。与高斯分布相关的一个重要定理是中心极限定理,它的内容为:任何分布的抽样分布当样本足够大时,其渐进分布都是高斯分布。高斯分布的密度函数为
其中数学期望值

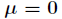
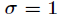
论文链接:http://www.doc88.com/p-0814329057281.html
接下来根据高斯分布的概率密度函数来推导期望。过程如下
有关高斯分布的文章:http://www.itongji.cn/article/111313452012.html








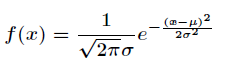
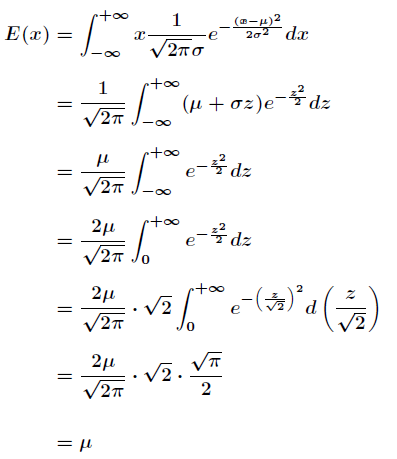
















 3121
3121

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








