干货！图像集分类大杀器--混合黎曼度量学习

AITIME论道

于 2021-09-25 20:11:15 发布

阅读量779

点赞数 3

文章标签：大数据算法编程语言 python 计算机视觉

原文链接：https://mp.weixin.qq.com/s?__biz=MzIzOTAxOTk3Nw==&mid=2247494899&idx=1&sn=28dd6e9f0c639fb25f798b2079fb6f33&chksm=e932de55de4557431600d02750be3060ab0327482cf6ff7b1e8522776847a66a9abca29edb60&scene=126&&sessionid=0

版权

点击蓝字

关注我们

AI TIME欢迎每一位AI爱好者的加入！

随着视频数据量的不断增加，图像集分类近年来受到了计算机视觉和模式识别研究社区的广泛关注。然而，表征的类内多样性和类间模糊性仍然是重大挑战。为了解决这一问题，研究人员提出了多种方法进行多重几何感知的图像集建模和学习。虽然提取的互补几何信息对决策是有益的，但这种算法的复杂计算范式（如散点矩阵计算和迭代优化）则需要付出较大的代价。

为此，本文提出了一种有效的混合黎曼度量学习框架。具体而言，作者设计了一种多图嵌入引导的度量学习框架，将通过格拉斯曼流形、SPD流形和高斯嵌入黎曼流形的显式 RKHS 嵌入得到的互补核特征融合到统一的子空间中进行分类。

此外，本文建立的模型所涉及的优化问题可以通过一系列子问题来解决，从理论上和事实上都提高了效率。本文作者进行了大量的实验来评估本文提出的方法的有效性。实验结果表明，该方法优于目前最先进的方法。

近年来，随着媒体数据的快速增长，图像集/视频识别在模式识别和计算机视觉领域受到越来越多的关注。与传统的单张图像分类任务不同，图像集包含多个实体，在集合内和集合间具有不同的外观变化，为建模图像集度量带来了复杂的挑战。

针对这一问题，研究人员通过探索非欧几里得结构来表示和度量图像集（如基于黎曼的分类器）。斯蒂费尔流形、格拉斯曼流形、对称正定流形（SPD）和高斯流形是计算机视觉领域常用的黎曼流形研究对象。然而，这些流形的非欧几里得性质使许多在欧几里得空间中具有良好性能的优秀的判别度量失效。因此，研究人员为这些流形设计了许多黎曼度量，如仿射不变黎曼度量（AIM）、Burg 矩阵散度、对数欧几里德度量（LEM）、Stein 散度、alpha-beta 散度和投影度量（PM）。通过使用这些度量，我们可以将一些欧氏建模技术泛化到黎曼空间中。

研究人员尝试使用定义好的黎曼核将流形隐式映射到一个再生核希尔伯特空间（RKHS）。由于 RKHS 是一个内积空间，可以通过核方法利用基于向量的分类器。之前的研究人员试图通过核方法融合多个异构几何，讨论了在平坦的欧几里得空间上生成黎曼流形的局部近似的切线映射运算。然而，上述两种黎曼方法间接地模拟了流形，却牺牲了固有的几何信息。为此，研究人员建议直接对黎曼流形进行降维，得到具有改进判别特征的低维子流形。此外，不能忽视图嵌入在机器学习社区中的有效性。研究人员试图通过直接建立在 SPD 流形上的稀疏图来学习更加鲁棒的度量。为了保持原有的流形结构，研究人员提出了一种新的基于自适应邻域的线性空间嵌入聚类方法。为了生成高质量的图，研究人员提出了一种鲁棒秩约束稀疏学习方法，该方法构造初始图并在其邻域内搜索。除了黎曼流形的基本数学模型，受最近深度学习框架所取得进展的启发，研究人员尝试构建深度黎曼网络，以更好地利用黎曼深度特征。由于其层级化的非线性学习机制，黎曼深度网络在分类任务中取得了显著的成功。

在本文中，作者提出了一种新颖的度量学习框架。如图 1 所示，该框架将多重黎曼图嵌入用于图像集分类。现有的方法大多应用单一流形对数据建模，而本文提出的方法则使用多个混合且互补的几何。此外，本文提出的算法的注意力图会引导模型重点关注收益最大的样本对，从而提升了计算效率。具体而言，作者首先将每个图像集编码到三个流形上（格拉斯曼、SPD、高斯流形），并将每个流形隐式地映射到 RKHS 中。为了更好地从高维希尔伯特空间中保留内在结构和判别性的信息，作者在每个希尔伯特空间中构建一个稀疏的连接图嵌入，突出数据分布的几何特性和概率特性。最后，作者通过核方法进行降维，从而得到低维空间中的聚合距离。大量的实验结果证明，本文提出的距离度量可以有效地为基于相似度的分类器捕获最近的具有代表性的邻居。

本文的主要贡献如下：

（1）提出根据三种黎曼流形推导出有效的距离度量。由于考虑了不同流形编码的信息的多样性，即使使用简单的最近邻分类器，本文提出的距离在视觉识别任务中也取得了性能提升。

（2）在另一个希尔伯特空间中构建编码内在几何信息的多图嵌入，从而关注收益最高的样本对。此外，提出了一种优化泛来高效地对图进行学习。

（3）与如今最优的黎曼方法相比，理论分析和实验验证都证明了本文提出方法的计算优势，尤其是本文提出的方法比其它混合黎曼方法的计算效率更高。这主要归功于图的稀疏性和优化的划分。

图 1：混合黎曼图嵌入度量学习（HRGEML）框架，其中不同的颜色表示不同的真实值，而不同的形状代表不同的样本。(a)首先输入图像集和提取到的特征度量(b)。(c)每个通过线性子空间、高斯分布和协方差矩阵描述的特征矩阵会被映射到格拉斯曼流形 G(q,d)、高斯流形、SPD 流形上(d)采用三种黎曼核将每个流形映射到希尔伯特空间中，在每个希尔伯特空间中构建稀疏关联图来引导模型融合收益最大的样本对，从而融合异构的几何(e)设计图嵌入度量学习框架将混合空间融合到低维但更具判别性的子空间中。

方法

在本章中，作者将首先介绍用到的各种黎曼描述子，接着会介绍基于图嵌入的黎曼度量学习框架。

各种黎曼描述子令为第 i 个图像集，包含 n_i 个样本，其中。从几何和统计的角度来说，本文作者利用了三种黎曼描述子来建模图像集。

格拉斯曼描述子

线性子空间具有计算复杂度较低、判别能力强等优点。对于 X_i 而言，可以通过谱分解得到其 q 维线性子空间：

其中，对角线上的值代表 q 个最大的特征值，是相对应的第 i 个正交的特征向量。Edelman 等人指出，该线性子空间落在一个格拉斯曼流形上。

协方差描述子

在不对数据分布做进一步假设的情况下，样本的协方差是一种广为使用的数据分布的描述子，它可以估计数据的变化情况。给定一个图像集 X_i ，其样本的协方差矩阵可以计算如下：

其中，μ^i 为 X_i 的均值向量，是一个中心化（centring）矩阵。Pennec 等人指出，协方差矩阵落在 SPD 流形上。

高斯描述子

在统计学中，由于同时捕获了数据集的一阶和二阶统计量，高斯分布成为了一种广为使用的概率分布。我们假设每个图像集都服从高斯分布。此外，通过如下所示的公式可将单模态高斯模型嵌入黎曼流形中：

混合黎曼度量

令为由 n 个图像集组成的训练集，其中代表包含 n_i 个实体的第 i 个图像集。受核方法成功的启发，为了处理异质黎曼特征，我们将黎曼核函数用于聚合互补特征。具体而言，一个核函数可以导出一个再生核希尔伯特空间 H，即。尽管计算过程中隐式地包含特征映射 Ψ，为了方便数学推导，我们将其视为显式的过程。令为从第 i 个图像集中提取到的第 r 个希尔伯特空间中的特征，通过相应的核函数从第 r 个流形推导得来。在这里，，当 R=3 时代表用到的三个流形特征。给定一对训练数据集 X_i 和 X_j，距离度量定义如下：

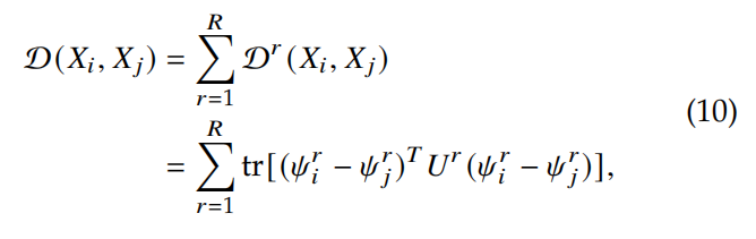
其中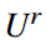，为第 r 个高维希尔伯特空间中学到的马氏矩阵。由于是对称正半定矩阵，我们可以将其分解为：，其中，为一个超定矩阵。因此，我们可以将上面的公式 (10) 改写为：

其中，。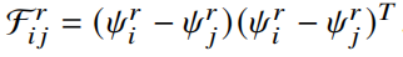

混合黎曼图嵌入

由于三个黎曼流形的几何性质不同，直接将它们组合起来是不合理的。为了掌握更多互补的有信息量的几何特性，我们需要在高维希尔伯特空间中构造具有几何特征和良好判别能力的多重图嵌入。另外，考虑到样本对的有效性，我们构造的图不应该是密集连通图。此外，对于稀疏选择的样本，它们的重要性应该是不同的。

从理论上讲，由于所有隐式地推导高维希尔伯特空间的核函数都是由流形推导出来的，我们假设在相应的希尔伯特空间中，可以保留某些几何结构。具体而言,一个 n 维流形，是一个拓扑空间，空间中的每个点都有一个邻居，同胚于 n 维欧氏空间。我们希望可以在某种程度上保留这种拓扑性质。在构图方面，LLE 通过计算低维、保邻的嵌入成功地实现了这一目标。然而，由于以下两种原因，通过 LLE 构建出的图并不具有足够的说服力：（1）得到的权重可能为负，并不适用于构图（2）LLE 只能给出线性重构权重，这与我们期望得到的相似度不同。为了解决上述问题，我们设计了一种概率单纯形约束。对于第 r 个希尔伯特空间，我们通过如下所示的公式得到邻居之间的相似度：

其中，为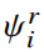在第 r 个希尔伯特空间中的 k 个最近邻居，为 k*1 的列向量，所有项均为 1，为非负权值，即第 i 个实体和第 j 个实体之间的相似度，为第 r 个希尔伯特空间中的第 i 张图像。此外，由于每个权值向量都在一个概率单纯形上，我们可以将视为一个条件变量，即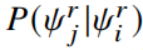。构建出的图为一个有向图。

关联函数 a(·,·):X×X→R 代表两个图像集之间的关联。具体而言，第 r 个希尔伯特空间中的类内相似度和类间相似度定义如下：

其中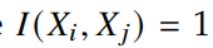，当且仅当 X_i 和 X_j 共享相同的标签。最近邻是根据在相应的希尔伯特空间中通过内积推导出的距离得出，可通过下面的核技巧计算：

其中，为第 r 个希尔伯特空间中的隐式特征，为内积，为第 r 个核矩阵中的第(i,j)个元素。

我们可以通过每个希尔伯特空间中的关联函数构建一个关联图：

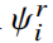其中，是第 r 个希尔伯特空间中从到的最终权值。

构建的关联图有以下特性：

（1）在公式(12)中，我们只关注邻居之间的相似度，实现了图连通的稀疏性。

（2）每个希尔伯特空间都是由不同的度规（即几何上异构的种类的内积）定义的，混合黎曼图嵌入保留了不同流形的集合信息。

（3）实现了注意力机制，即更加关注具有较大相似度的样本对。

目标函数

一般来说，给定公式(11)表示的距离和公式(16)表示的图，我们希望在降维后最小化类间的相似性，最大化类内的紧凑性。幸运的是，在我们的稀疏关联图中编码了少数对之间的重要关系。因此，我们为第 r 个流形寻找一个嵌入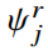，这样一来，点对之间的关联就可以通过低维空间上的相似性度量来反映。这个想法与帕累托原则不谋而合，即对于许多结果来说，大多数结果是由少数原因造成的。具体而言，集合

且集合中的样本对来自相同的类，样本对中一个样本是另一个样本第 k 个最近的邻居，而则并不要求样本来自同一个类。类内和类间的损失函数如下：

其中，，全局目标函数为：

实验

作者在 Virus、MDSD、CG、FPHA、UCF-sub 共 5 个数据集上对本文提出的方法的有效性和效率进行了深入的分析。

VIrus 数据集包含 15 种不同的病毒，共有 150 个透射电镜（TEM）图像块。该数据集中类内和类间都有很大的模糊性。病毒的形状和尺寸各异，类内图像的分辨率、不清晰的轮廓信息差异很大。

马里兰动态场景数据集（MDSD）中每类包含 10 段视频，共包含 13 类不同的动态场景。在分辨率，光照情况，视角，以及相机动态方面的剧烈变化，使这个数据集非常具有挑战性。

剑桥手势（CG）数据集由 900 段视频序列组成，被分类为 9 类手势，每一类手势包含 100 个动作片段。

UCF-101 数据集由来自 Youtube 的超过 1.3 万个视频片段组成，总时长超过 27 小时，共包含 101 类动作。

FPHA 数据集包含 1,175 个动作视频，共涉及 45 类不同的动作，是用于基于骨架的第一人称人手动作估计的对比基准。

图 2：（a）Virus 中的 TEM 病毒图像（b）MDSD 中的动态场景示例（c）CG 中的手势样例（d）UCF-101 中的视频帧（e）FPHA 中的图像

作者将本文提出的方法与以下基线进行了对比：SPD 流形学习（SPDML-AIM, SPDML Stein）、格拉斯曼判别分析（GDA）、投影度量学习（PML）、协方差判别学习（CDL）、对数欧氏度量学习（LEML）、混合欧几里得黎曼度量学习（HERML）、多流形度量学习（MMML）、SPD 网络（SPDNet）、格拉斯曼网络（GrNet）、SymNet 以及多重黎曼多核度量学习（MRMML）。

表 1：各种对比基线在 Virus、MDSD、CG、UCF 数据集上的分类准确率