K-hidden

K-hidden算法

1. 信息负表示

• 负表示的概念由Esponda等人于2004年首次提出。
• 信息负表示是由生物免疫系统中的负选择机制启发得到。
• 负调查、负数据库是信息负表示的主要模型之一。

2. 负调查

• 负调查（Negative surveys）是一种隐私保护技术，可以在不获取用户的真实问卷调查的情况下来分析调查数据。
• 目前有两大类负调查方式，主要分为均匀负调查（UNSs）和高斯负调查（GNSs）。
  

3. 负数据库

• 负数据库是信息负表示的一个重要模型。
• 正数据库（Positive database ，DB） ：传统的数据库
• 负数据库（Negative database ，NDB ）：由Esponda等人于2004年提出DB的补集的压缩表示全集U = {0, 1}
  
  负数据库（NDB）：
• 通配符‘*’可任意表示‘0’、‘1’
• 确定位0、1;不确定位*
• 使用‘*’压缩补集U-DB
• NDB的大小可压缩到合理的范围，如O(DB)
  
  隐藏串：DB中的原始数据（即需要隐私保护的数据）
• 将与隐藏串对应位相同的确定位称为取正位，反之则叫做取反位。
• 根据隐藏串的个数：单串负数据库、多串负数据库。

4. 负数据库生成算法
   
   4.1 q-hidden算法
   利用一个参数q控制负数据库中不同类型的记录分布。
   具体步骤：

• 随机生成一条与隐藏串有相同位数的记录，
  每一条记录都有3个确定位。
• 如果生成的记录与隐藏串有i(1≤i≤3）位不匹配，则负数据库以q[i]的概率接受该条记录。
  q-hidden算法对于典型的SAT求解器Zchaff和
  WalkSAT都是难解的，但q-hidden算法生成算法生成的负数据库不是完备的。
  4.2 K-hidden算法
  参考文献：赵冬冬. 信息负表示的若干应用方案研究[D].中国科学技术大学,2016.
  
• 当 K=3 时，K-hidden 算法就等价为 q-hidden 算法 。
• 由文献定理2.1，当 K-hidden 算法满足以下条件时，其所生成的负数据库对于局部搜索策略是难以逆转的。
  
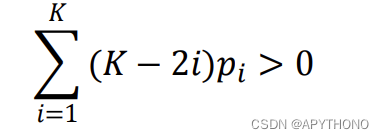
  总结出 K-hidden 算法所生成的负数据库的特点如下：
• 负数据库中一共有 m × r条记录。
• 每一条记录都有 K 个确定位。
• 负数据库中出现第 i 种类型的记录的概率为 p[i] 。
  理论分析和实验结果表明：K>3时，能获得更难解的负数据库，且可控性更强！

K-hidden算法实现

import random as rd

NDBs = list()

flag = 0
print('请输入隐藏串：')
s = input()
while (flag == 0):
    if s[0] == "0":
        print('输入隐藏串错误，应该以1开头,请重新输入')
        s = input()
    else:
        flag = 1
m = len(s)
print("隐藏串s的长度是{}".format(m))
print("请输入常量K(K<隐藏串长度m)")
K = int(input())
while (K >= m):
    print("K超过隐藏串长度，请重新输入常量K：")
    K = int(input())
print("请输入控制NDB的大小参数r(推荐6.5)")
r = float(input())
print("请输入概率参数,长度为{}，请保证所有概率和为1".format(K))
p = list(map(float, input().split()))
print("二进制串为{},串长为{}\n常量K为{},控制参数r为{}\n概率参数为{}".format(s, m, K, r, p))

# NDB总数
N = int(float(m) * r)
print("NDB中的记录总数为{}".format(N))

# 生成Q
count = 0
Q = list()
for i in range(K):
    count = count + float(p[i])
    Q.append(count)

ndbs = 0
count_dic = dict()
while (ndbs < N):
    rnd = rd.random()
    for i in range(1, K + 1):  # 从1到K,找概率
        if Q[i - 1] <= rnd < Q[i]:
            # i为统计类型，有i类生成的与隐藏串有i个不同i的范围为1到K

            place = set()

            for num in range(K):  # 找K个随机位置并且记录在place中作为最终的确定位
                a = rd.randint(0, m)
                while (a in place):
                    a = rd.randint(0, m)
                place.add(a)

            # place 有K个元素，从中选i个出来加入dif_place，这i个位置与隐藏串不匹配
            dif_place = set()
            p_list = list(place)
            for num in range(i):
                b = rd.randint(0, K - 1)
                while (p_list[b] in dif_place):
                    b = rd.randint(0, K - 1)
                dif_place.add(p_list[b])

            # 生成负数据库数据
            elem = ''
            for sc in range(m):  # 遍历m次
                if sc in dif_place:
                    if s[sc] == '0':
                        elem = elem + '1'
                    else:
                        elem = elem + '0'
                else:
                    if sc in place:
                        elem = elem + s[sc]
                    else:
                        elem = elem + "*"

            NDBs.append(elem)
            break
    ndbs = ndbs + 1
    print("记录第{}条数据".format(ndbs))
print(NDBs)
f = open("ndbs.txt","w")
for data in NDBs:
    f.write(data)
    f.write('\n')