杨辉三角形

原创已于 2023-04-05 17:06:31 修改 · 205 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #java #c++

于 2023-04-05 10:28:48 首次发布

题目描述

下面的图形是著名的杨辉三角形：

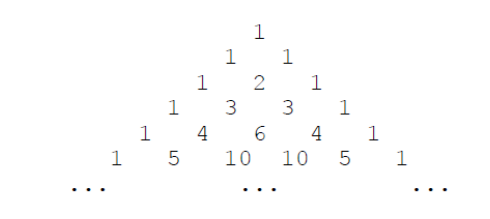
如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下数列： 1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, \cdots1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,⋯

给定一个正整数 NN，请你输出数列中第一次出现 NN 是在第几个数？

输入描述

输入一个整数 NN。

输出描述

输出一个整数代表答案。

输入输出样例

示例 1

输入

输出

评测用例规模与约定

对于 20%20 的评测用例，1\leq N\leq 101≤N≤10；对于所有评测用例，1\leq N\leq 10000000001≤N≤1000000000。

解析

暴力算法，遍历所有情况，需要设置条件来减少运行时间

#define _CRT_SECURE_NO_WARNINGS//暴力
#include<stdio.h>
#include<stdlib.h>
//核心在于排列组合，其次是如何减少不必要的遍历

long C(long a,long b,long n)//C排列组合算法
{
  long res=1;//一开始要赋值为1！
  for(long i=a,j=1;j<=b;i--,j++)//一个循环就可以实现C排列组合
  {
    res=res*i/j;
  if(res>n)
  {
    return res;
  }//放循环里判断！优化算法
  //一旦这个res在循环中的结果已经有了超过n的就马上退出，不要再
  //等它全部遍历完返回再判断！
  }

  return res;

}

int main()
{
    long n, i, t = 100000000;
    ////x数据大你也放int 真服了
    //以后记住，如果不确定数据大不大，宁愿放long long也不放int
    //i会使得大的数据溢出错误，自己放int还是long一定要想好,包括循环里的变量
    int num = 1, flag = 0;
    long long int x;//数据大
    scanf("%ld", &n);
    if (n == 1)
    {
        printf("1");
        return 0;
    }

    for (i = 1; flag != 1; i++)
        //i就是当前数字的行位
        //注意i的大小，一开始是1，当这一次循环结束之后下一次就是二
        //所以当循环结束之前，使用的i其实是i-1,结束后才是真正的i。
    {
       
        num = 1;
        //数字在该行中的位置,也是列，每次新的一行就重置
        for (long j = 1; j <= i / 2 && j < t; j++)
            //j的作用就是将i分为两半，用于排列组合Cj/i,表格中就是Cj/i的规则,j最大不过i的一半
            //因为左右两边对称，只有中间的数才是最大的
            //涂色区域的每一个数都是符合c几几的
            //j<t是为了后面缩小范围,优化算法,不写等于是因为不会比t大
                                                
            
        {
            num++;
            //每次循环加1，相当于往右移一位
        //j与Num匹配，第二位就j=1,第三位就j=2
            // x = 1;//初始化x
            // for (long k = 0; k < j; k++)//这个算法太low了
            //     x *= (i - k);
            // for (long k = 0; k < j; k++)
            //     x /= (k + 1);
           
             
             
             x=C(i,j,n);//排列组合
           

            if (x == n)
            {
                flag = 1;
                break;
            }

            if (x > n)//本可以不写，但是会超时
            {
                t = j;
                //数字只会因为循环越来越大
                //发现这一行的这个数超过我要的，我就跳出循环到下一行，
                // 因为后面只可能更大或者对称，根本不可能会有
                //而根据表格增长倍数，后面会越来越大，肯定不会超过当前的j，
                //即当前的位置
                //这是优化算法

                break;
                //当前的x比n大就跳出当前行数到下一行
                //t=j是标记现在数的位置
                //如果还没有到第三位数字，就继续一直下一行
                //直到到第三位还超过就说明只可能在第二位
                //此时就直接确定n在第n行
                //而此时下底长度为n+1
            }
        }
        if (t == 2)//本可以不写，但是会超时,跟前面一样的，只不过减少了运行时间
        //t==2是第三列的数，因为我们有第0列
        {
            num = 2;
            i = n+1;         
            //行数和下底的长度是有关系的！
    //i+1就是当前行数的下底长度，所以为了得出下底长度要增加1
           
           //前面是在j循环跳出的，然后默认判断flag==1跳出循环
           //但是i会再循环中加1
           //但是在i循环判断t==2跳出是不会增加i的
           //所以为了对应i要增加的情况就要在i=n的基础上
           //在加1即i=n+1       
           //记住我们算的要得出的是下底的长度，而不是行数
           //下底的长度不等于行数！
  
            break;
        }//不写超时，提前退出程序，最坏的情况,观察三角形可知，最坏的情况只可能是第二个数字出现.
        //如果j=2就是第三位就超过了，那只可能在数位第二
        //第三位超过不一定就在下一行，必须要根据规律


        //优化算法很重要！特别是数据庞大的时候，其实x>n和t==2这两个本来都可以不用写，但是运行时间就会很长
        //超时就输出不了答案，因此就要学会技巧优化算法，主要还必须对模型理解的足够深刻才行
    }
    //最后循环结束完毕后就执行了i++,如执行时i一直等于4，结束循环以后回过循环时就会加上这个++
    //变为5，即i(该行数）

    printf("%ld", num +i*(i-1) / 2);
    //这个是上面的面积，当前行的数字个数由num确定，而前面的面积就一定是固定的了
    //所以这里是求上一行的下底,所以下底为i-1。
    //实际上是梯形，因为上面1就相当于长度为1，而不是三角形，所以实际上就是梯形面积

      //((i-1)+1)*(i-1)/2,是面积，也可以理解为等差数列

  
    return 0;
}
//细化条件来防止运行超时，优化算法
//2.想清楚你要求的数据是什么！
//3.循环的逻辑一定要清楚,如何执行，如果要用到循环变量

这里是一个例子说明循环变量的值的问题

#include <iostream>
using namespace std;
int main()
{
	int i;
	for (i = 0; i < 10; i++)
	{
		if (i == 5)
			break;
	}

	cout << i << endl;
	int flag = 0;

	for (i = 0; flag!=1; i++)
	{
		for(int j=0;j<10;j++)
			if (i == 5)
			{
				flag = 1;
               break;
		}
			
	}

	//直接break循环，循环的变量就不会在结尾的时候增加，但是没有break就会依次判断
	//先判断条件，如flag!=1决定是否继续循环,但是否继续循环都不会影响i++的执行
	//而break就是直接跳出循环，不再执行所有的判断

	cout << i;
	return 0;
}

可以看到在J循环中跳出i是增加了的，而这就刚刚好对应了下底长度,因此出了循环以后就i的值就是下底，而在i循环break，i不会增加，所以要自己加1变为下底.

二分

//二分法解

//流程：最大列->起点行->2k--n之间究竟哪一行（二分+排列组合）->找到行数就等差数列+对应位置

#include<stdio.h>
#include<stdlib.h>

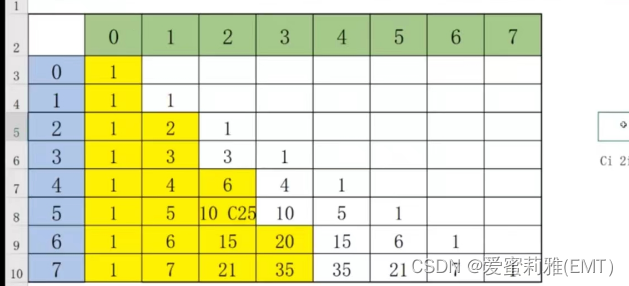
//注意排列组合的规律是建立在第0行和第0列的基础！
long C(long a,long b,long n)//C排列组合算法
{
  long res=1;//一开始要赋值为1！
  for(long i=a,j=1;j<=b;i--,j++)//一个循环就可以实现C排列组合
  {
    res=res*i/j;
  if(res>n)
  {
    return res;
  }//放循环里判断！优化算法
  //一旦这个res在循环中的结果已经有了超过n的就马上退出，不要再
  //等它全部遍历完返回再判断！
  }

  return res;

}

    
	int main(int argc, char *argv[])
	{
	  long n,k;
	  scanf("%ld",&n);    
	  // for(k=0;;k++)err
	   for(k=16;k>=0;k--)
	   //为什么正着输出不行
	   //因为我们是计算第一次出现的数字
	   //那就必须要在最后面的列开始找
	   //一直往前面的列逐个寻找
	   //你从正着遍历就是直接输出最近的也就是第1列
	   //第一列必会出现这个数的答案，因此直接输出了
	   //就不是第一次出现
	   //所以不可以不计算

	  //k代表需要遍历列数
    //这是根据最大测评数据推出的,1e9
    //计算器难计算的，就可以借助编程来计算
    //自己写一个排列组合的函数，该题也用到了这个函数
    //代数看看最大只可能出现在哪即可
    //求出最大列数不可能在17列，C17/34大于1e9
    //因此可以得知在[0,16]之间


    
    
	  //k--能写成k++，肌肉记忆是吧?
	  {
	    long l=2*k,r=n;
	    //l等于2k是对应行数
	    //因为一开始从最大列开始算
	    //也就只有2k以后的行才会有这么多的有效列
	    //所以从这以后开始查找
	    //l是需要遍历的行数,
	    //这里等于2k仅仅只是满足最大情况
	    //当最大情况不为所求时就用二分法
	    //矫正行数，这就是为什么二分法只分行数
	    //列不变，也是定一动一.

	    //int mid=(l+r)/2;
	    //这个要放里面，因为每次二分都是不同位置的！
	   
    while(l<=r) //二分法
    //二分法可以是mid值作为想要输出的结果
    //也可以使用right和left作为想要的输出结果
    //具体不同题设判断如何用l,r还是mid
    //当结果不用l、r时，我们就不需要考虑
    //l与r究竟谁赋值mid了。直接舍弃即可(求Mid)
    //因为我们要求的只有唯一值就是行数
    //所以可以直接使用mid
    //直接用mid就是固定的
    //  r=mid-1;
    //  l=mid+1;
    //类似的模板
    //(因为既然mid值都不为所求,自然都舍弃)

       //l是左边界，r是右边界(我们求行数所以左边界为l)
       //意思就是从l的范围开始找
       //而r是上限，
      //所寻找的行永远小于等于n行，所以可以设边界
       //最差的情况就是数字等于行数
          //即所找的数字在第n行第二位的情况
          //所以r=n
         
    {
       long mid=(l+r)/2;//划分中点
       //我们的二分法是为了寻找所求数字的
       //所在的行和列，而不是直接找到该数字！
       
      if(C(mid,k,n)==n)//mid是所寻找的行不是数字
      //中点恰好是要找的行
      //放在全局变量就不用上传这么多参数了

	        {
	          printf("%ld",(1+mid)*mid/2+k+1);
	          //这里是等差数列，每一行的全部是
	          //d=1的等差，1+2+3+......
            //注意我们求的是数字数量之和不是大小之和
	          //所以(a1+an)*n/2
	        
            //这里的等差数列是把原来的第0列看成第一列了
         //这里的等差数列就没有第0列
            //因此求出来的mid行数就是上一行
            //恰好可以排等差数列,剩下的加上k+1即可
            //k+1是因为排列组合有第0列，既然是在使用这个
            //规律的基础上，就必须遵循第0列开始，
            //而第0列->k列就是k+1

            //注意过程的选取，是等差数列的过程
            // 还是处在排列组合的过程
	 
           
         
	          return 0;
      
      }
      else if(C(mid,k,n)>n)
      r=mid-1;
      //mid太大就只可能在左边一堆，
      //然后循环再分一次
      else//mid太小
      l=mid+1;

    }

  }
  return 0;
}