浮点数——

1、纠正两个错误

第一个是讲结构体的时候，说结构体的大小是成员数乘以最大对齐数是错的，结构体的大小是最大对齐数的整数倍，另外结构体嵌套结构体在算大小时是按结构体成员算的，不是用嵌套在结构内的结构体整体大小算的。

第二个就是

这不叫柔性数组

这个才叫柔性数组

2、关于malloc、calloc和relloc

先看一个代码

为什么会报错？

因为malloc申请的是堆区的空间，而全局变量是在静态区，造成了冲突，所以会报错，另外用static修饰的变量也不能用malloc申请空间，因为static修饰的变量是放在静态区的，calloc和relloc也是一样的。

（这个不是重定义的错）

realloc在扩容时有可能会换地址，如果使用了realloc来扩容，那么在内存中观察时要记得重新取地址。

3、关于浮点数

c语言的库函数中有一个pow函数，平时算次方时都喜欢用它算，它的参数和返回值都是double类型，但是我们传参数时传入整型它也可以算，也能用整形接受。这个是有风险的。

先看浮点数的存储

浮点数是用科学计数法来计算的，存的是二进制，S用来计算符号位，E是指数位，M是尾数。

E在存储时会加上127（float是127，double,1023）。

M实际上是1<=M<2的数，但是实际存的只存小数部分，算的时候再加上1。

计算方法x=(-1)^S*M*2^(E-127)(float是E-127，double是E-1023)。

（0.5实际是二进制1.0*2^(-1)其中E=126，S=0，M=0）

另外如果指数部分的二进制全为0（加完127或1023后），那么实际的E=1-127（double是1-1023），全为1表示无穷大，因为可能溢出了，浮点数还有精度的问题。

、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、

说回pow函数，如果你用它计算很大的数字是会有精度的问题

例如：

你说他会不会打印“x=y”

因为2^54=18,014,398,509,481,984，这个数字非常大，用科学计数法会搞出一个很长的小数double的精度不够，导致它计算出现了问题。解决方法是强制类型转换，但这也不是万全之策，

最好就是不要用它来计算很大的整形，如果要算大数就用快速幂算法来算。

. - 力扣（LeetCode）

4、一个和浮点数存储有关的算法

平方根倒数快速算法 

1、牛顿迭代法求平方根

如果我们要求一个数 K 的平方根，我们可以看成是求 y=x*x-k 函数与 x 轴的交点的横坐标。

牛顿迭代法就是先取一个近似值，做这个点的切线，找出切线 x 轴的交点的横坐标 x1 ，再把 x1 带入y=x*x-k，再做切线，再找出切线 x 轴的交点的横坐标 x2 ，重复的找切线与x 轴的交点的横坐标，迭代次数越多， x 就越接近 k 的平方根。

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <math.h>
// 牛顿迭代法求解平方根函数
float newton_sqrt(float number, float guess, float epsilon) {
    float new_guess;
    do {
        // 使用牛顿迭代法更新猜测值
        new_guess = 0.5 * (guess + number / guess);

        // 检查是否满足精度要求
        if (fabs(new_guess - guess) < epsilon) {
            return new_guess;
        }

        guess = new_guess;
    } while (1);  // 无限循环，直到满足精度要求才退出
}
int main() {
    float number = 25;  // 要求解平方根的数
    float guess = 1.0;  // 初始猜测值
    float epsilon = 0.0001;  // 误差容限

    // 使用牛顿迭代法求解平方根
    float sqrt_approx = newton_sqrt(number, guess, epsilon);

    // 输出结果
    printf("牛顿迭代法求得的平方根近似值为: %f\n", sqrt_approx);

    return 0;
}

可以看到如果我们要获得精确的值就要用循环，那我们可不可以用一次牛顿迭代法就得出精确值

那我们首先就要得到一个精切的近似值。

2、浮点数表示

前面说了浮点数 y=(-1)^S*M*2^(E-127) ,由于算平方根所以是 y=M*2^（E-127）；如果尾数的二进制序列表示数字 m，那 M 又可以写成M=1+m/(2^23),也就是说M=1+m/（2^23），

y=（1+（m/2^23））*2^（E-127）

3、对数

如果我们假设 k 的平方根倒数为A，那么 logA=-1/2logk (log是以2为底)

先看logk，logk=log（（1+（m/2^23））*2^（E-127））=  log（1+（m/2^23））+E-127；

而M=1+（m/2^23），且1<=M<2;

又因为log（1+x）和 x 在（0,1）范围的时候值是相近的，所以我们用 x 来近似代替 log（1+x）

所以logk=m/2^23+E-127=(m+E*2^23) / (2^23)-127 

一个神奇的地方

假设这个整数是Y

所以logk=Y/(2^23)-127;

所以logA=-1/2(Y/2^23-127)，把logA也换一下（假设A的二进制序列表示整数a）

a/(2^23)-127 = -1/2(Y/2^23-127),把a表示出来a=381*（2^22）- Y/2,把a算出来，再把a的二进制序列当成浮点数计算，得出k的平方根近似值，再用牛顿迭代法提高精度。

381*（2^22）的16进制为0x5f400000，如果用这个值算的话只有在区间（0,1）的头尾非常精确

中间误差比较大，于是做了修正，用0x5f3759df来算。

这个是网上的代码：

float fast_inverse_sqrt(float number) {
    long i;
    float x2, y;
    const float threehalfs = 1.5f;

    x2 = number * 0.5f;
    y = number;
    i = *(long*)&y;            // 将浮点数的位级表示转换为整数

    // 利用常数0x5f3759df和位级操作进行近似计算
    i = 0x5f3759df - (i >> 1);
    y = *(float*)&i;           // 将整数的位级表示转换回浮点数

    // 牛顿迭代法优化近似值
    y = y * (threehalfs - (x2 * y * y));

    return y;
}

但是我用这个代码并不能算出一个数的平方根，那是因为y是平方根的倒数，少了一步。

这才是完整的：

float fast_inverse_sqrt(float number) {
    long i;
    float x2, y;
    const float threehalfs = 1.5f;

    x2 = number * 0.5f;
    y = number;
    i = *(long*)&y;            // 将浮点数的位级表示转换为整数

    // 利用常数0x5f3759df和位级操作进行近似计算
    i = 0x5f3759df - (i >> 1);
    y = *(float*)&i;           // 将整数的位级表示转换回浮点数

    // 牛顿迭代法优化近似值
    y = y * (threehalfs - (x2 * y * y));
    y = 1 / y;

    return y;
}

y = y * (threehalfs - (x2 * y * y));这个是怎么来的呢

其实是用这个函数y=A-k^(-1/2)来算的，令y=0；得A=k^(-1/2)，进而得k=1/(A*A),

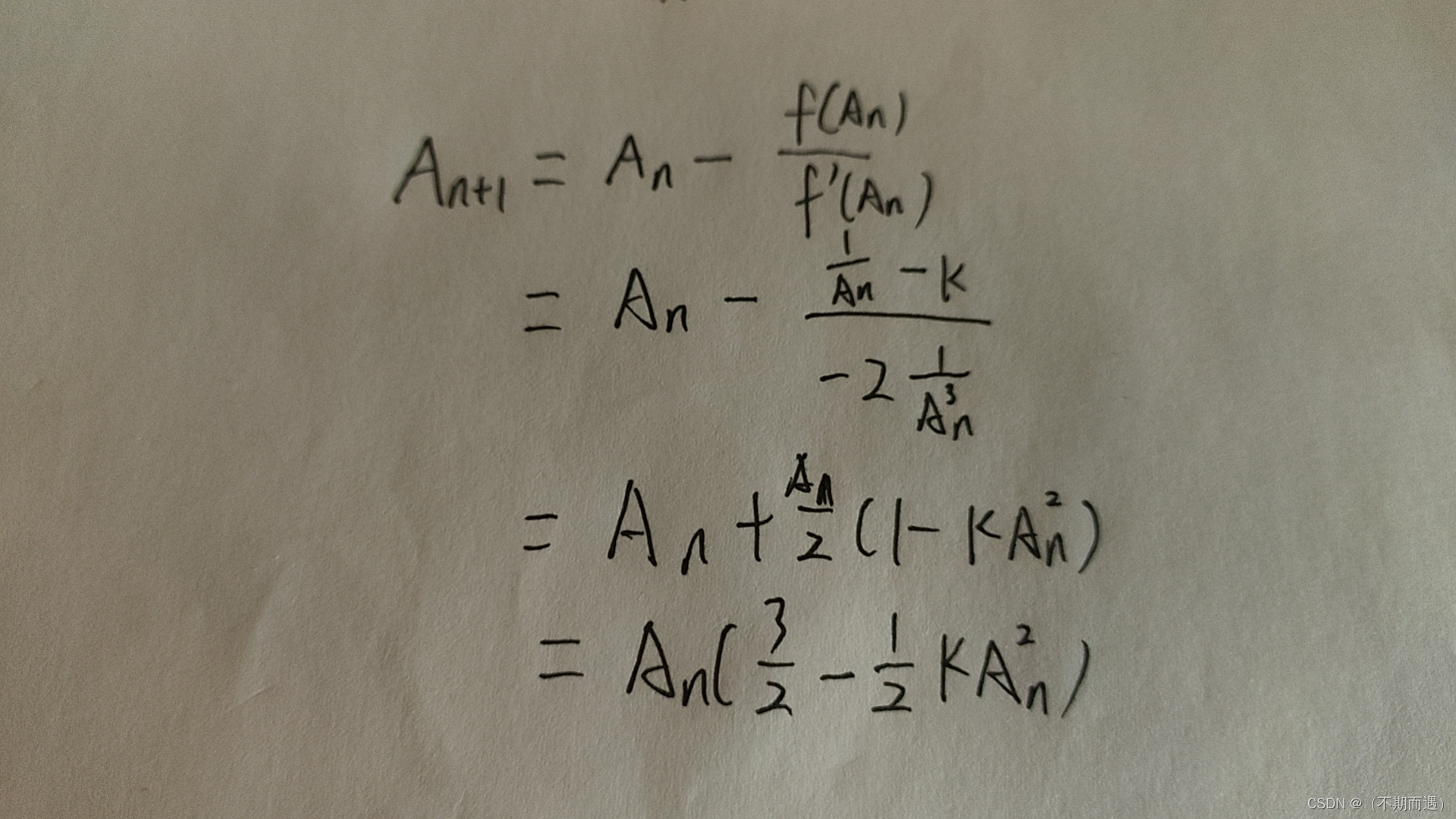
其实这感觉没什么意义，结尾的除法是一定要的，要不然算不出平方根， 用这个y=x*x-k是一样的，而且精度更高。

其实我一开始学的时候写的是这个

float q_rsqrt(float number)
{
    int i = 0;
    float x2 = 0.0f, y = 0.0f;
   /* const float threehalfs = 1.5f;*/
    x2 = number * 0.5f;
    y = number;
    i = *(long*)&y;
    i = 0x1FC00000 + (i >> 1);
   /* i = 0x5f3759df - (i >> 1);*/
    y = *(float*)&i;
   /* y = y * (threehalfs - (x2 * y * y));*/
    y = y * 0.5 + x2 / y;
    /*y = y * 0.5 + x2 / y;*/

    return y;
}

没有取倒数

我用库函数做了对比

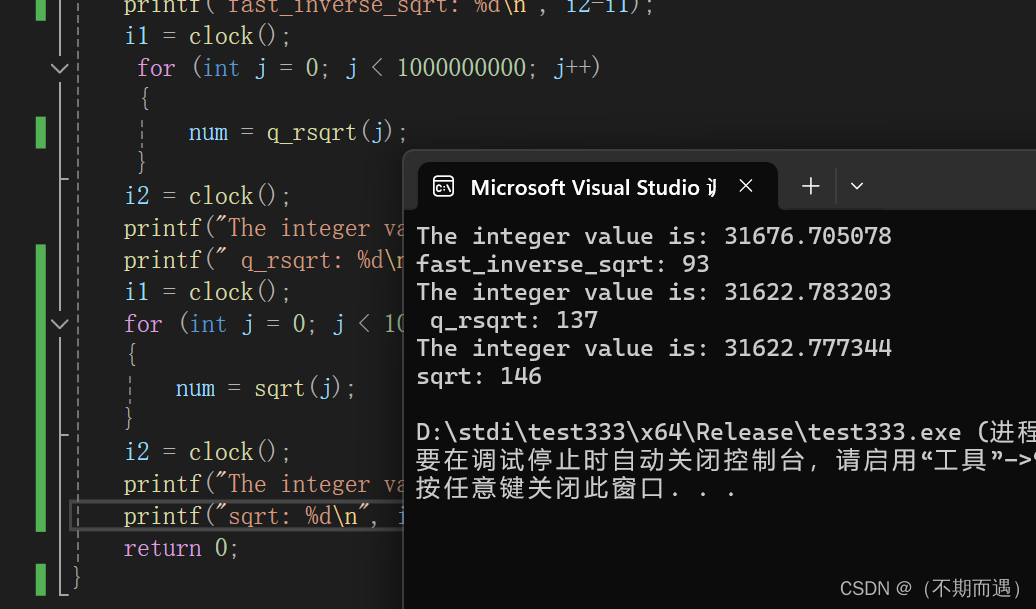
在Releas版本下计算1000000000次的速度和精度对比。

第一个是网络版本、第二个是我写的、第三个是库函数

当然网络版本这个程序是用于游戏的，不需要非常高的精度，可以去了解这个算法的故事

float fast_inverse_sqrt(float number) {
    long i;
    float x2, y;
    const float threehalfs = 1.5f;

    x2 = number * 0.5f;
    y = number;
    i = *(long*)&y;            // 将浮点数的位级表示转换为整数

    // 利用常数0x5f3759df和位级操作进行近似计算
    i = 0x5f3759df - (i >> 1);
    y = *(float*)&i;           // 将整数的位级表示转换回浮点数

    // 牛顿迭代法优化近似值
    y = y * (threehalfs - (x2 * y * y));
    y = 1 / y;

    return y;
}
float q_rsqrt(float number)
{
    int i = 0;
    float x2 = 0.0f, y = 0.0f;
   /* const float threehalfs = 1.5f;*/
    x2 = number * 0.5f;
    y = number;
    i = *(long*)&y;
    i = 0x1FC00000 + (i >> 1);
   /* i = 0x5f3759df - (i >> 1);*/
    y = *(float*)&i;
   /* y = y * (threehalfs - (x2 * y * y));*/
    y = y * 0.5 + x2 / y;
    /*y = y * 0.5 + x2 / y;*/

    return y;
}
int main() {
    float num=0.0f;
    int i1 = clock();
    for (int j = 0; j < 1000000000; j++)
    {
        num = fast_inverse_sqrt(j);
    }
    int i2 = clock();
    printf("The integer value is: %f\n", num);
    printf("fast_inverse_sqrt: %d\n", i2-i1);
    i1 = clock();
     for (int j = 0; j < 1000000000; j++)
     {
         num = q_rsqrt(j);
     }
    i2 = clock();
    printf("The integer value is: %f\n", num);
    printf(" q_rsqrt: %d\n", i2-i1);
    i1 = clock();
    for (int j = 0; j < 1000000000; j++)
    {
        num = sqrt(j);
    }
    i2 = clock();
    printf("The integer value is: %f\n", num);
    printf("sqrt: %d\n", i2 - i1);
    return 0;
}

 后面继续数据结构，时不时发布其他的