用N皇后问题深入理解几种架构风格_n皇后管道过滤器-CSDN博客

本文链接：https://blog.csdn.net/Accepted_Lam/article/details/102516571

本文通过N皇后问题探讨四种不同的架构风格：管道/过滤器、调用/返回、回溯法和黑板风格。分别分析设计、实现与优化，并通过类图展示各自特点。性能对比显示，回溯法和调用/返回风格在时间复杂度上表现优秀，而黑板风格因线程切换开销较大，时间随皇后数量增加明显。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

这次的软件架构作业要求是分别使用管道/过滤器风格，调用/返回风格，回溯法，和黑板风格四种方法实现N皇后问题，并比较这四种实现方案的性能
那么话不多说，就开始我们的介绍吧

N皇后问题描述

N皇后问题描述的是如何将n个皇后放置在n*n的棋盘上，并使n个皇后不会互相攻击，即他们不能同行，不能同列，也不能位于同一条对角线上。我们要做的，就是在给定N的情况下算出有多少种满足情况的棋局。这道题是一个非常经典的问题了，但是我们在这里并不着重于解释N皇后问题的思路，而是用这个例子去深入研究不用的架构风格

分别使用不同的架构风格实现N皇后问题

管道/过滤器风格

首先让我们来看看什么是管道过滤器风格

管道过滤器风格管道/过滤器风格是指在程序中的一个处理流程中，过程元素的输出是下一个过程元素的输入，连续的过程元素中使用字节或者位的缓冲量作为连接两个过程元素的中间数据流。
要注意的是，每个过滤器(也就是上面提到的过程元素)是独立的，不能与其他的过滤器共享数据，同时这个过滤器也不知道其他过滤器的存在，也就是他们之间是解耦的。一个管道过滤器网络输出的正确性并不依赖于过滤器进行增量计算过程的顺序。

总结一下就是管道过滤器风格有以下几个特点：

它是由数据控制计算的
系统结构由数据在处理之间有序移动
数据流结构的系统有明显的结构
进程之间除了数据交换，没有任何其他的交互

分析与设计

讲完了管道/过滤器风格，接下来让我们结合N皇后问题进行分析:

通过N皇后的问题描述中我们可以知道，对于一个棋局棋局，要满足N皇后问题的要求，那么这个棋盘需要同时满足如下5个条件:
a. 恰好有N个皇后
b. 对于该棋盘中的每一列，有且仅有一个皇后
c. 对于该棋盘中的每一行，有且仅有一个皇后
d. 对于该棋盘中的每一条主对角线，有且仅有一个皇后
e. 对于该棋盘中的每一条副对角线，有且仅有一个皇后
如果有其中一个条件不符合，那么这个棋局就不满足问题的要求。

根据上面对问题的分析，我们可以知道，N皇后问题实际上可以认为是5个条件的判断，5个条件的判断是互相不干扰的，只有同时满足了5个条件才能满足N皇后问题的要求
那么现在，按照管道/过滤器的术语来描述需求:
给定四个条件的过滤器，遍历一个含有N个皇后的棋局，将同时符合5个条件(也就是5个过滤器)的所有棋局过滤出来

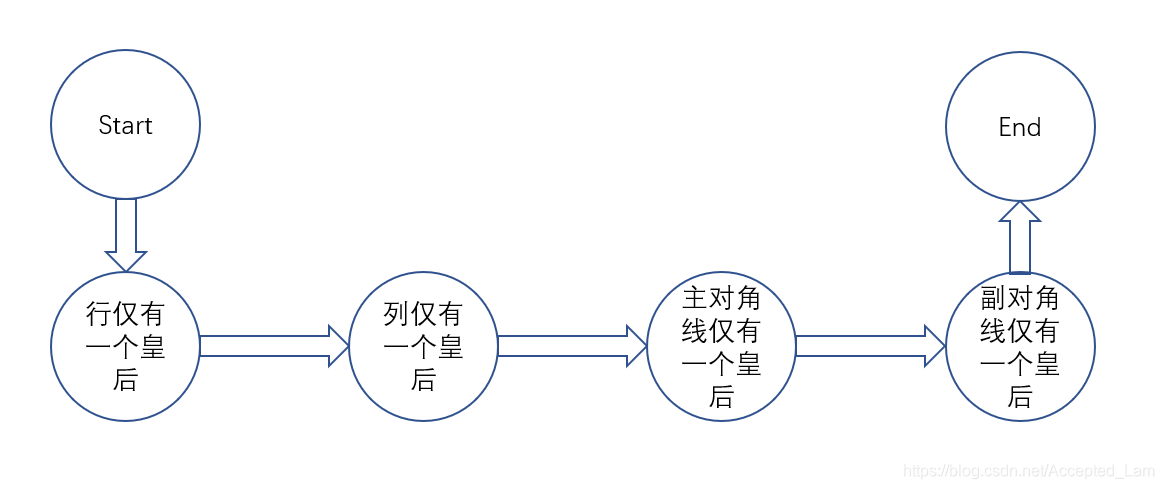
在这里插入图片描述
这幅图描述了管道/过滤器使用，其中箭头代表数据流的流向，圆圈代表不同的进程/方法。
在实现的时候我们需要对于N*N的棋盘生成所有的情况（相当于全排列），然后对于每一个棋局进行逐一判断

实现与优化

类图如下，使用startuml进行绘制
在这里插入图片描述
其中四种Filter(AmountFilter,ColumnFilter,LineFilter,MainDagonalFilter,ParaDiagonalFilter)继承父类Filter,代表一个判断的条件。
过滤器的代码如下，使用java实现:



public class Filter {
   
       boolean judge(boolean[][] c) {
   
    	   return false;
       }
}

class AmountFilter extends Filter{
   
	public boolean judge(boolean[][] c) {
   
		int len = c.length;
		int amount = 0;
		for(int i = 0;i < len; i++) //计算皇后总数
			for(int j = 0;j < len ;j++)
				if(c[i][j] == true)
					amount++;
		if(amount == len) return true;
		else return false;
	}
}

class ColumnFilter extends Filter{
   
	public boolean judge(boolean[][] c) {
   
		int len = c.length;
		boolean flag = false;//用来记录第i行是否已经有一个皇后了
		for(int i = 0;i < len; i++) {
   
			flag = false;
			for(int j = 0; j < len;j++) {
   
				if(flag == false && c[j][i] == true)
					flag = true;
				else if(flag == true && c[j][i] == true)
					return false;//说明一列有两个皇后
			}
		}
		return true;
	}
}

class LineFilter extends Filter{
   
	public boolean judge(boolean[][] c) {
   
		int len = c.length;
		boolean flag = false;//用来记录第i行是否已经有一个皇后了
		for(int i = 0;i < len; i++) {
   
			flag = false;
			for(int j = 0; j < len;j++) {
   
				if(flag == false &