一些分布图

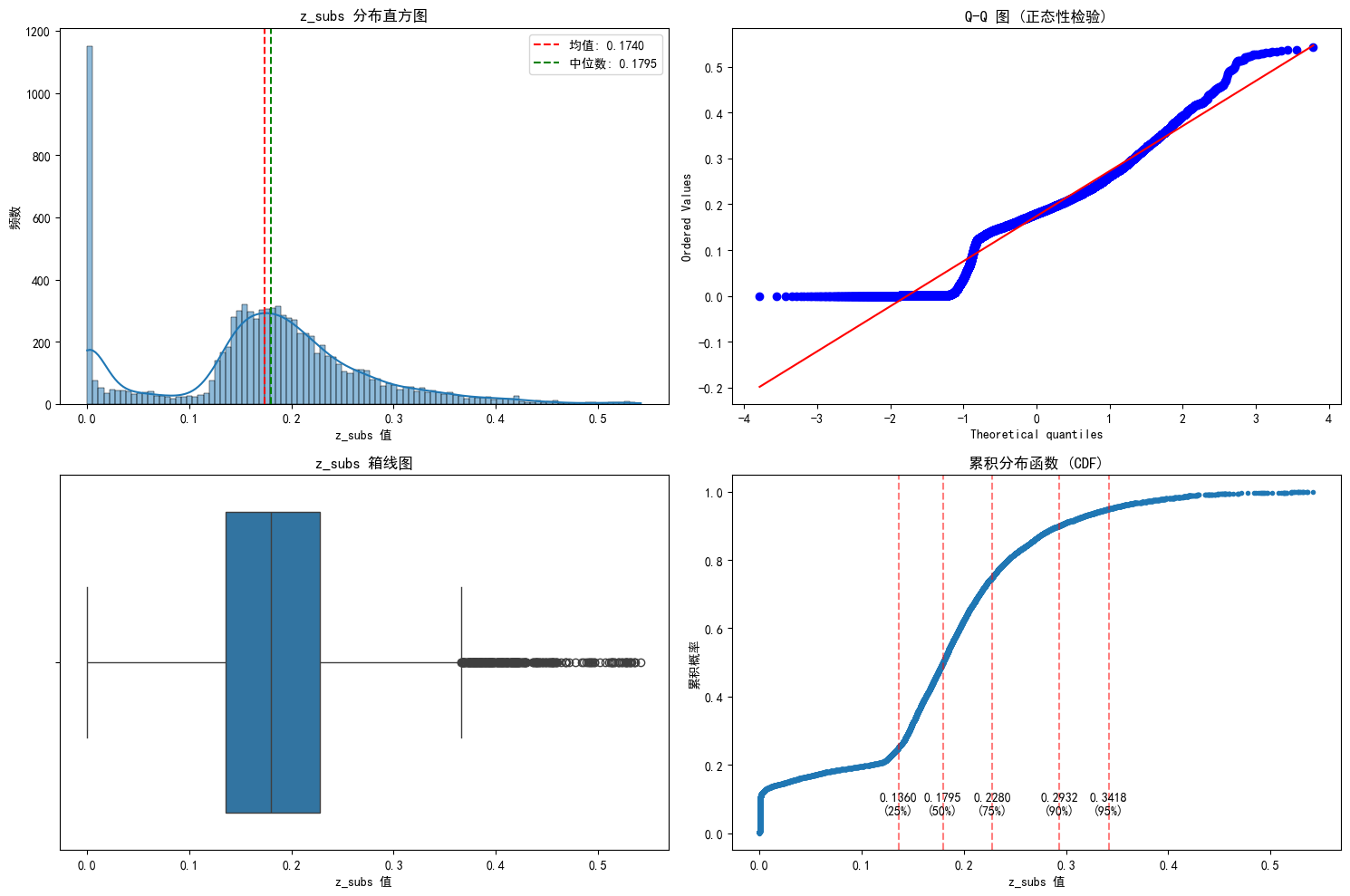
分析图详解

这四个图从不同角度展示了z_subs值的分布特征，帮助我们全面理解模型输出的概率分布情况。下面我详细介绍每个图的含义和解读方法：

1. 直方图与密度曲线 (Histogram with Density Curve)

含义：

• 直方图：将数据范围分成若干个区间（bin），用条形高度表示每个区间内数据点的数量
• 密度曲线：平滑地展示数据分布的概率密度函数（Probability Density Function, PDF）

如何解读：

1. 分布形状：

   • 对称分布：图形左右对称，峰值在中间（如正态分布）
   • 偏态分布：
     • 右偏（正偏态）：右侧尾部较长，均值 > 中位数
     • 左偏（负偏态）：左侧尾部较长，均值 < 中位数
   • 多峰分布：出现多个峰值，表示数据可能来自不同群体

2. 中心位置：

   • 红色虚线（均值）和绿色虚线（中位数）的位置关系
   • 当均值 > 中位数 → 右偏分布
   • 当均值 < 中位数 → 左偏分布

3. 离散程度：

   • 图形越"宽扁"，数据越分散
   • 图形越"瘦高"，数据越集中

4. 异常值：

   • 远离主分布区域的孤立条形可能表示异常值

2. Q-Q图 (Quantile-Quantile Plot)

含义：

• 比较数据分布与理论正态分布的分位数
• 横轴：理论正态分布的分位数
• 纵轴：实际数据的分位数

如何解读：

1. 正态性检验：

   • 如果数据点基本落在对角线上 → 符合正态分布
   • 偏离对角线越多 → 偏离正态分布越远

2. 分布类型判断：

   • S形曲线：厚尾分布（数据极端值比正态分布多）
   • 凸形曲线：轻尾分布（数据极端值比正态分布少）
   • 直线但斜率≠1：位置参数不同
   • 直线但截距≠0：尺度参数不同

3. 异常值识别：

   • 远离对角线的点可能是异常值

3. 箱线图 (Box Plot)

含义：

• 五数概括：最小值、第一四分位数(Q1)、中位数、第三四分位数(Q3)、最大值
• 箱体：包含50%的数据（Q1到Q3之间）
• 须线：延伸到1.5倍IQR（四分位距）内的最远点
• 异常值：超出须线的点

如何解读：

1. 中心位置：

   • 箱体中的中位线表示数据的中位数

2. 离散程度：

   • 箱体高度（IQR）表示中间50%数据的离散程度
   • 须线长度表示数据范围的离散程度

3. 偏态判断：

   • 中位线在箱体中央 → 对称分布
   • 中位线靠近箱体底部 → 右偏分布
   • 中位线靠近箱体顶部 → 左偏分布

4. 异常值检测：

   • 须线外的点都是潜在的异常值

4. 累积分布函数 (Cumulative Distribution Function, CDF)

含义：

• 表示随机变量取值小于或等于某个特定值的概率
• 横轴：z_subs值
• 纵轴：累积概率（从0到1）

如何解读：

1. 分布特征：

   • 曲线陡峭上升：数据集中在该区域
   • 曲线平缓：数据稀疏区域

2. 分位数定位：

   • 垂直方向：找到概率值P
   • 水平方向：找到对应的z_subs值
   • 例如：90%分位数表示90%的数据点小于该值

3. 比较分布：

   • 曲线越靠左：数据整体值较小
   • 曲线越靠右：数据整体值较大

4. 阈值选择：

   • 想覆盖90%的数据 → 选择90%分位数对应的z_subs值
   • 想保留高置信度预测 → 选择95%或99%分位数

综合解读技巧

1. 一致性检查：

   • 直方图的中位数/均值应与箱线图的中位线一致
   • CDF的50%分位数应与中位数一致
   • Q-Q图的偏离模式应与直方图的偏态一致

2. 阈值选择指导：

   • 保守阈值（高召回率）：选择较低分位数（如10%或25%）
   • 平衡阈值：选择中位数（50%）
   • 严格阈值（高精确率）：选择较高分位数（如90%或95%）

3. 模型诊断：

   • 高度偏态分布 → 可能需要转换或特殊处理
   • 多峰分布 → 数据可能来自不同群体，需分层处理
   • 大量异常值 → 可能需要异常检测或数据清洗

4. 决策支持：

   • 结合业务目标选择阈值
     • 避免漏报（如医疗诊断）：选较低阈值，提高召回率
     • 避免误报（如垃圾邮件过滤）：选较高阈值，提高精确率