仅供参考,请独立完成。
基本要求: 每个题目的解答应包含必要的解题分析、源程序、结果和答案。 要把解决问题的过程、思路写清楚。(模块一除外)
模块一:基础练习
教学要求:熟练掌握 Matlab 软件的基本命令和操作,会作二维、三维几何图形,能够用 MATLAB 软件计算数学分析中函数的极限、微分、积分、Taylor 展开和级数和高等代数及解析几 何中的相关问题
※ 特别要求 在下面的题目中,1-4 班 m 为你学号的后 3 位,00 班 m 为你学号的后 2 位+70)。
1
计算limx→01+mx2−cosmxx2\lim_x\to0\frac{\sqrt{1+mx^{2}}-\cos mx}{x^{2}}limx→0x21+mx2−cosmx和limx→∞1+mx2−cosmxx2.\lim_x\to\infty\frac{\sqrt{1+mx^{2}}-\cos mx}{x^{2}}.limx→∞x21+mx2−cosmx.
代码:
m = 83;
syms x;
limit1 = limit((sqrt(1 + m*x^2) - cos(m*x))/x^2, x, 0);
limit2 = limit((sqrt(1 + m*x^2) - cos(m*x))/x^2, x, Inf);

2
计算
(1)∫0+∞e−mx2dx\int _{0}^{+ \infty }e^{- mx^2}dx∫0+∞e−mx2dx
(2)∫01/2ex2dx\int _{0}^{1/ 2}e^{x^2}dx∫01/2ex2dx (精确到 17 位有效数字)
(3)∫mx425+4x2dx\int\frac{mx^4}{25+4x^2}dx\quad∫25+4x2mx4dx
(4) ∫−11(∫−1−x21−x21−x2 dy)dx\:\int_{-1}^{1}(\int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}}\sqrt{1-x^2}\:dy)dx∫−11(∫−1−x21−x21−x2dy)dx
(5)利用符号积分计算∫−3π1.6πe−∣x∣∣sinx∣\int_{-3\pi}^{1.6\pi}e^{-|x|}|\sin x|∫−3π1.6πe−∣x∣∣sinx∣具有 64 位精度的值。
m = 83;
syms x y;
int(exp(-m*x^2), x, 0, Inf)
vpa(int(exp(x^2), x, 0, 1/2), 17)
int((m*x^4)/(25 + 4*x^2), x)
int(int(sqrt(1 - x^2), y, -sqrt(1 - x^2), sqrt(1 - x^2)), x, -1, 1)
vpa(int(exp(-abs(x))*abs(sin(x)), x, -3*pi, 1.6*pi), 64)
3
将函数f(x)=xcos(x)f(x)=x\cos(x)f(x)=xcos(x)在x=0x=0x=0点进行 Taylor 展开Tn(x)T_n(x)Tn(x),对不同 n 观察Tn(x)T_n(x)Tn(x)与f(x)f(x)f(x)的逼近程度有什么变化。
syms x
f = x*cos(x); % 定义函数
x_vals = linspace(-2*pi, 2*pi, 1000); % 定义x的取值范围
figure
hold on
fplot(f, [-2*pi, 2*pi], 'LineWidth', 2) % 绘制原函数
colors = ['r', 'g', 'b', 'm', 'c'];
for n = 1:5
T = taylor(f, x, 'Order', n); % 进行 Taylor 展开
fplot(T, [-2*pi, 2*pi], colors(n)) % 绘制 Taylor 多项式
end
legend('f(x)', 'T_1(x)', 'T_2(x)', 'T_3(x)', 'T_4(x)', 'T_5(x)')
title('Taylor Approximation of f(x) = xcos(x) at x = 0')
hold off
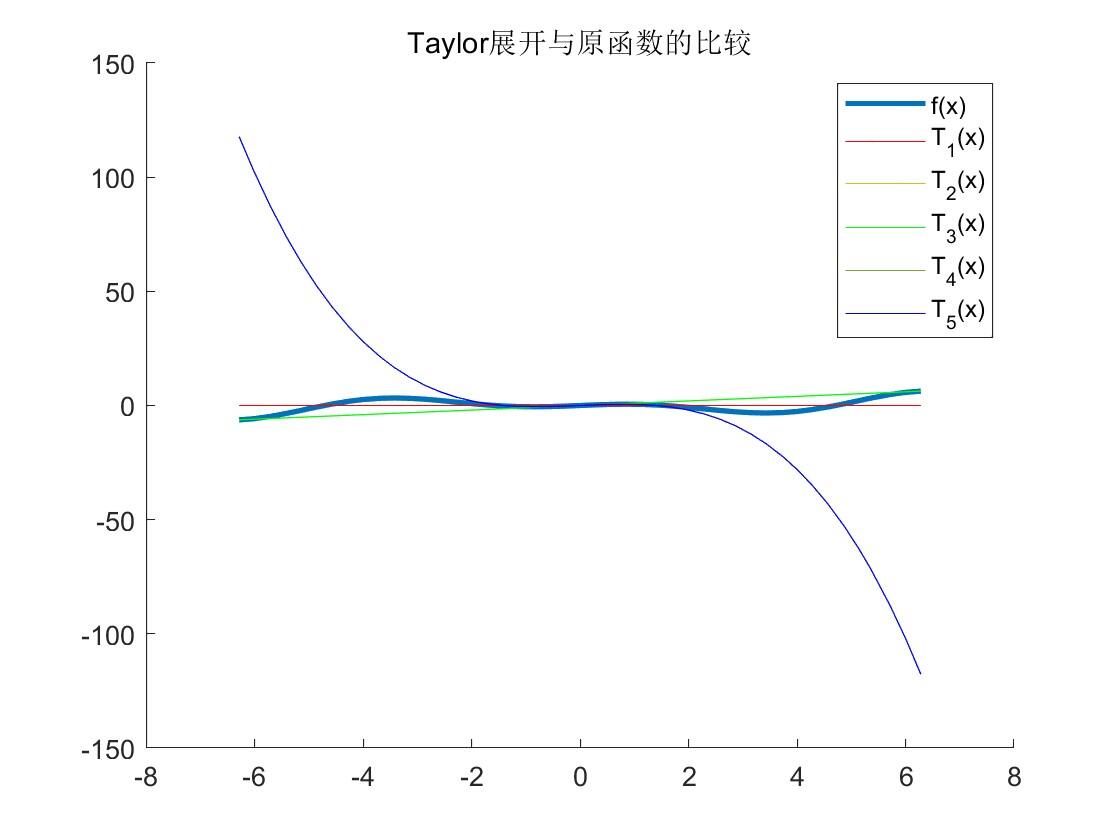
4
(1)求使得∑n=21nlnn>10\sum_n=2\frac{1}{\sqrt{n}\ln n}>10∑n=2nlnn1>10的最小的正整数 M;(2)不使用循环计算∑n=11000nsin(n)2n\sum_n=1^{1000}\frac{n\sin(n)}{2^{n}}∑n=110002nnsin(n)。
% (1) 求使得 ∑(n=2)^(M) 1/(√n * ln(n)) > 10 的最小正整数 M
M = 2; % 初始值
sum_value = 0;
while sum_value <= 10
sum_value = 0;
for n = 2:M
sum_value = sum_value + 1/(sqrt(n) * log(n));
end
M = M + 1;
end
M = M - 2; % 最小满足条件的 M
disp(['最小满足条件的 M 值为:', num2str(M)]);
% (2) 不使用循环计算 ∑(n=1)^(1000) n*sin(n)/(2^n)
n = 1:1000;
sum_value = sum(n .* sin(n) ./ (2 .^ n));
disp(['∑(n=1)^(1000) n*sin(n)/(2^n) 的值为:', num2str(sum_value)]);

5
(1) 设f(x)=excosf( x) = e^{x}\cosf(x)=excos (m100x2+x+1)( \frac m{100}x^{2}+ x+ \mathbf{1} )(100mx2+x+1), 求f′′(x)f^{\prime\prime}(x)f′′(x)和f(10)(0)f^{(10)}(0)f(10)(0)。
syms x;
m = 78;
f = exp(x) * cos(m/100 * x^2 + x + 1); % 定义函数 f(x)
f_double_prime = diff(f, x, 2); % 计算 f''(x)
f_10th_derivative = diff(f, x, 10); % 计算 f^(10)(x)
% 计算 x = 0 时的 f''(x) 和 f^(10)(x) 的值
f_double_prime_at_0 = subs(f_double_prime, x, 0)
f_10th_derivative_at_0 = subs(f_10th_derivative, x, 0)

(2)计算∂2∂x2(x2e−y),∂2∂x∂y(x2e−y)∣x=1,y=2\left.\frac{\partial^{2}}{\partial x^{2}}(x^{2}e^{-y}),\frac{\partial^{2}}{\partial x\partial y}(x^{2}e^{-y})\right|_{x=1,y=2}∂x2∂2(x2e−y),∂x∂y∂2(x2e−y)x=1,y=2.
syms x y
% 定义函数
f = x^2 * exp(-y);
% 计算二阶偏导数
d2f_dx2 = diff(f, x, 2);
d2f_dxdy = diff(diff(f, x), y);
% 代入 x=1, y=2
d2f_dx2 = simplify(d2f_dx2)
d2f_dxdy_value = subs(d2f_dxdy, [x, y], [1, 2])
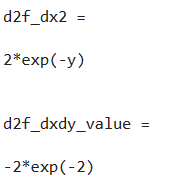
6
已知矩阵A=(4−22−305150.1m),B=(134−20−32−11)A=\begin{pmatrix}4&-2&2\\-3&0&5\\1&5&0.1m\end{pmatrix},B=\begin{pmatrix}1&3&4\\-2&0&-3\\2&-1&1\end{pmatrix}A=4−31−205250.1m,B=1−2230−14−31,计算 A 的行列式、逆矩阵、特征值和特征向量,An,AB−1,A−1BA^n,AB^{-1},A^{-1}BAn,AB−1,A−1B。
m = 83;
A = [4, -2, 2; -3, 0, 5; 1, 5, 0.1*m];
B = [1, 3, 4; -2, 0, -3; 2, -1, 1];
% 计算 A 的行列式
det_A = det(A);
disp('行列式 det(A) = ');
disp(det_A);
% 计算 A 的逆矩阵
inv_A = inv(A);
disp('逆矩阵 inv(A) = ');
disp(inv_A);
% 计算 A 的特征值和特征向量
[eig_vec_A, eig_val_A] = eig(A);
disp('特征值 eig_val_A = ');
disp(eig_val_A);
disp('特征向量 eig_vec_A = ');
disp(eig_vec_A);
% 计算 A 的幂 A^n
n = 2; % 替换为你想要计算的幂
A_pow_n = A^n;
disp(['A 的幂 A^', num2str(n), ' = ']);
disp(A_pow_n);
% 计算 AB^(-1)
AB_inv = A * inv(B);
disp('AB^(-1) = ');
disp(AB_inv);
% 计算 A^(-1)B
A_invB = inv(A) * B;
disp('A^(-1)B = ');
disp(A_invB);
d2f_dxdy_value = subs(d2f_dxdy, [x, y], [1, 2])

7
求下列向量组的一个极大无关组,并用其表示其它向量:
α1=(−5,−1,−5,−1,5)\alpha _{1}= ( - 5, - 1, - 5, - 1, 5)α1=(−5,−1,−5,−1,5), α2=(−2,2,−10,2,10)\alpha _{2}= ( - 2, 2, - 10, 2, 10)α2=(−2,2,−10,2,10), α3=(−3,3,−5,3,5)\alpha _{3}= ( - 3, 3, - 5, 3, 5)α3=(−3,3,−5,3,5),
α4=(0\alpha _{4}= ( 0α4=(0, 1, -1, 1, 1), α5=(−1,1,−11,1,11)\alpha _{5}= ( - 1, 1, -11, 1, 11)α5=(−1,1,−11,1,11)。
function vectorProperties(V)
% 求向量组的秩
r = rank(V);
fprintf('向量组的秩为: %d\n', r);
% R: 行化简后的阶梯型; j: 主元
[R, j] = rref(V);
% 打印最大线性无关组
fprintf('最大线性无关组为:\n');
disp(V(:,j));
num_vectors = size(V, 2);
for a = setdiff(1:num_vectors, j)
% 输出当前向量的编号
fprintf("a%d用该最大无关组线性表示为\n", a);
term_count = 1;
% 遍历当前向量对应的系数
for b = R(:, a)'
if b ~= 0
% 格式化输出系数和向量编号
if b > 0 && term_count ~= 1
fprintf("+%d*a%d", round(b), term_count)
else
fprintf("%d*a%d", round(b), term_count)
end
% 更新向量编号
term_count = term_count + 1;
end
end
fprintf("\n");
end
end
a1 = [-5; -1; -5; -1; 5];
a2 = [-2; 2; -10; 2; 10];
a3 = [-3; 3; -5; 3; 5];
a4 = [0; 1; -1; 1; 1];
a5 = [-1; 1; -11; 1; 11];
A = [a1,a2,a3,a4,a5];
vectorProperties(A);

8
(1)将二次型f(x1,x2,x3,x4,x5)=4x12+11x1x2+4x22+11x2x3+4x32+11x3x4+4x42+11x4x5+4x52f(x_1,x_{2},x_{3},x_{4},x_{5})=4x_{1}^{2}+11x_{1}x_{2}+4x_{2}^{2}+11x_{2}x_{3}+4x_{3}^{2}+11x_{3}x_{4}+4x_{4}^{2}+11x_{4}x_{5}+4x_{5}^{2}f(x1,x2,x3,x4,x5)=4x12+11x1x2+4x22+11x2x3+4x32+11x3x4+4x42+11x4x5+4x52用正交变换化为标准二次型并写出及对应的正交变换。
% 定义二次型的矩阵
A = [4 5.5 0 0 0;
5.5 4 5.5 0 0;
0 5.5 4 5.5 0;
0 0 5.5 4 5.5;
0 0 0 5.5 4];
% 计算A的特征值和特征向量
[V, D] = eig(A);
% 特征向量矩阵V就是正交变换矩阵
disp('正交变换矩阵:')
disp(V)
% 特征值矩阵D的对角线元素就是标准二次型的系数
disp('标准二次型的系数:')
disp(diag(D))

(2) 用两种不同的方法求方程组的通解:{x1+2x2−3x3−x4=12x1−x2−x3+4x4=4x1+4x2−7x3−5x4=−1\begin{cases}x_{1}+2x_{2}-3x_{3}-x_{4}=1\\2x_{1}-x_{2}-x_{3}+4x_{4}=4\\x_{1}+4x_{2}-7x_{3}-5x_{4}=-1\end{cases}⎩⎨⎧x1+2x2−3x3−x4=12x1−x2−x3+4x4=4x1+4x2−7x3−5x4=−1
A = [1 2 -3 -1;
2 -1 -1 4;
1 4 -7 -5];
b = [1; 4; -1];
x = linsolve(A, b)
A_inv = inv(A);
% 使用矩阵乘法求解方程组
x = A_inv * b

9
作出如下函数的图形
(1)f(x)={2x,0≤x≤122(1−x),12<x≤1f(x)=\begin{cases}2x,&0\leq x\leq\frac{1}{2}\\2(1-x),&\frac{1}{2}<x\leq1\end{cases}\quadf(x)={2x,2(1−x),0≤x≤2121<x≤1(2)f(x)={3x−2x≤−π4arctanx+sinx−π4≤x≤π4lnxx≥π4\quad f(x)=\begin{cases}3x-2&x\leq-\frac{\pi}{4}\\\arctan x+\sin x&-\frac{\pi}{4}\leq x\leq\frac{\pi}{4}\\\ln x&x\geq\frac{\pi}{4}\end{cases}f(x)=⎩⎨⎧3x−2arctanx+sinxlnxx≤−4π−4π≤x≤4πx≥4π
% 问题1
figure(1);
x1 = 0:0.01:0.5;
y1 = 2 * x1;
x2 = 0.5:0.01:1;
y2 = 2 * (1 - x2);
plot([x1, x2], [y1, y2]);
% 问题2
figure(2);
x1 = -10:0.01:-pi/4;
y1 = 3 * x1 - 2;
x2 = -pi/4:0.01:pi/4;
y2 = atan(x2) + sin(x2);
x3 = pi/4:0.01:10;
y3 = log(x3);
plot([x1, x2, x3], [y1, y2, y3]);

10
作出面两条空间曲线的图像
(1){x=m20costy=m20sintz=t\begin{cases}x=\frac{m}{20}\cos t\\y=\frac{m}{20}\sin t\\z=t\end{cases}\quad⎩⎨⎧x=20mcosty=20msintz=t(2){x=cost+tsinty=sint−tcostz=−t−m≤t≤m\quad\begin{cases}x=\cos t+t\sin t\\y=\sin t-t\cos t\\z=-t\end{cases}\quad-m\leq t\leq m⎩⎨⎧x=cost+tsinty=sint−tcostz=−t−m≤t≤m
m = 83;
t = -m:0.01:m;
% 问题1
figure(1);
x1 = m/20 * cos(t);
y1 = m/20 * sin(t);
z1 = t;
plot3(x1, y1, z1);
title('x = m/20*cos(t), y = m/20*sin(t), z = t');
% 问题2
figure(2);
x2 = cos(t) + t.*sin(t);
y2 = sin(t) - t.*cos(t);
z2 = -t;
plot3(x2, y2, z2);
title('x = cos(t) + t*sin(t), y = sin(t) - t*cos(t), z = -t');

11
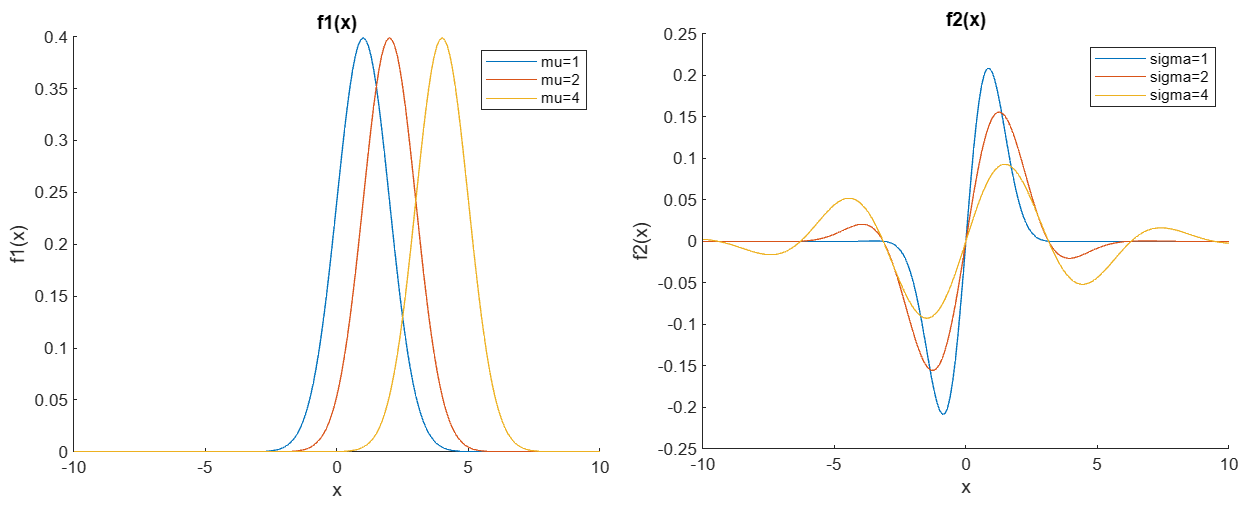
已知 f1(x)=12πσe−(x−μ)22σ2,f2(x)=sinx2πσe−(x−μ)22σ2f_1(x)=\frac1{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}},f_{2}(x)=\frac{sinx}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}}f1(x)=2πσ1e−2σ2(x−μ)2,f2(x)=2πσsinxe−2σ2(x−μ)2,分别在下列条件下画出f1(x),f2(x)f_1(x),f_2(x)f1(x),f2(x)的图形
(1)σ=1\sigma=1σ=1时, μ=1,2,4\mu = 1, 2, 4μ=1,2,4(在同一坐标系上作图) (2) μ=0\mu = 0μ=0时, σ=1,2,4\sigma = 1, 2, 4σ=1,2,4(在同一坐标系上作图)
% 清空变量和图形窗口
clear;clc;close all;
% 定义函数 f1(x) 和 f2(x)
f1 = @(x, mu, sigma) 1/(sqrt(2*pi)*sigma) * exp(-(x-mu).^2 / (2*sigma^2));
f2 = @(x, mu, sigma) sin(x) ./ (sqrt(2*pi)*sigma) .* exp(-(x-mu).^2 / (2*sigma^2));
% 绘制 f1(x) 和 f2(x) 的图形
x = -10:0.1:10; % x 的范围
mu_values = [1, 2, 4]; % 不同的 mu 值
sigma_values = [1, 2, 4]; % 不同的 sigma 值
% 绘制 f1(x) 的图形
figure;
hold on;
for i = 1:length(mu_values)
mu = mu_values(i);
f = f1(x, mu, 1);
plot(x, f);
end
legend('mu=1', 'mu=2', 'mu=4');
title('f1(x)');
xlabel('x');
ylabel('f1(x)');
hold off;
% 绘制 f2(x) 的图形
figure;
hold on;
for i = 1:length(sigma_values)
sigma = sigma_values(i);
f = f2(x, 0, sigma);
plot(x, f);
end
legend('sigma=1', 'sigma=2', 'sigma=4');
title('f2(x)');
xlabel('x');
ylabel('f2(x)');
hold off;
12
用 ezplot 命令画出由方程sin(x2+m2000y2)=cosxy\sin(x^2+\frac{m}{2000}y^2)=\cos xysin(x2+2000my2)=cosxy确定的隐函数的图形。
% 清空变量和图形窗口
clear;clc;close all;
m = 83;
f = @(x, y) sin(x.^2 + m/2000*y.^2) - cos(x.*y);
figure
ezplot(f, [-10, 10, -10, 10])
title('隐函数图形')
xlabel('x')
ylabel('y')

13
作出函数z=mx2+y4z=mx^2+y^4z=mx2+y4的曲面图
% 定义参数 m
m = 83;
x = linspace(-10, 10, 100);
y = linspace(-10, 10, 100);
[X, Y] = meshgrid(x, y);
Z = m*X.^2 + Y.^4;
figure
surf(X, Y, Z)
title('函数 z = m*x^2 + y^4 的曲面图')
xlabel('x')
ylabel('y')
zlabel('z')

14
写出y=x−xsin(3x)y=x-x\sin(3x)y=x−xsin(3x)(0≤x≤1\leq x\leq1≤x≤1)绕X轴形成的旋转曲面的参数方程并画出曲面图形。
% 清空变量和图形窗口
clear;clc;close all;
m = 83;
x = linspace(0, 1, 100);
theta = linspace(0, 2*pi, 100);
[X, Theta] = meshgrid(x, theta);
Y = (X - X.*sin(3*X)).*cos(Theta);
Z = (X - X.*sin(3*X)).*sin(Theta);
figure
surf(X, Y, Z)
title('函数 y = x - x*sin(3x) 绕 X 轴旋转形成的曲面')
xlabel('x')
ylabel('y')
zlabel('z')

模块二 函数与方程
教学要求:使学生能够熟练利用 MATLAB 求代数方程的解和非线性函数的零点
极大值、极小值以及常微分方程的解,并能够利用相关理论解决实际问题。
1
已知函数f(x)=x4−2xf(x)=x^4-2^xf(x)=x4−2x在(-2,2)内有两个根,计算函数的最小值点和两个根的近似解(精度自己定)。分别用如下方法求近似根:
1)根据 f(xi)*f(xi-1)<=0 用变步长搜索求近似根;
2)通过求函数绝对值的最小值点,找到两个近似根,在每个近似根附近通过缩小步长提高根的精度;
3)用 matlab 自带的函数求函数的最小值和两个近似根。
解题分析:
题目要求用以下三种方法来求解:
-
变步长搜索:这个方法的基本思想是在给定区间内以一定的步长搜索函数值的符号变化,当函数值的符号发生改变时,我们可以确定根存在于这两个点之间。
-
求函数绝对值的最小值点:这个方法的基本思想是找到函数绝对值的最小值点,这些点通常就是函数的根。然后在这些点附近缩小步长,以提高根的精度。
-
使用MATLAB自带的函数:MATLAB提供了一些内置函数,如fminbnd和fzero,可以用来求函数的最小值和根。
源程序:
% 定义函数
f = @(x) x.^4 - 2.^x;
% 方法1:变步长搜索
xi = -2;
step = 0.1; % 初始步长
while f(xi)*f(xi-step) > 0
xi = xi + step;
end
root1 = xi;
xi = 2;
while f(xi)*f(xi-step) > 0
xi = xi - step;
end
root2 = xi;
% 方法2:求函数绝对值的最小值点
step = 0.01; % 缩小步长
[min_val1, xi] = min(abs(f(-2:step:root1)));
root1_refined = xi*step - 2;
[min_val2, xi] = min(abs(f(root2:step:2)));
root2_refined = xi*step + root2;
% 方法3:使用MATLAB自带的函数
[min_val, min_point] = fminbnd(f, -2, 2);
root1_matlab = fzero(f, -2);
root2_matlab = fzero(f, 2);
% 输出结果
fprintf('方法1找到的近似根为:%f, %f\n', root1, root2);
fprintf('方法2找到的近似根为:%f, %f\n', root1_refined, root2_refined);
fprintf('方法3找到的近似根为:%f, %f\n', root1_matlab, root2_matlab);
fprintf('函数的最小值点为:%f, 最小值为:%f\n', min_point, min_val);
结果:

2
对于方程ex−3mm+100x2=0e^x-3\frac{m}{m+100}x^2=0ex−3m+100mx2=0,先画出函数在合适的区间上的图形,借助于软件中的方程近似求根的命令求出所有的根,并解释为什么你求出的根是方程所有的根。
解题分析:
先画出函数和导函数的图像,画出了函数的图像。通过观察图像,然后选择一个合适的初始猜测值。之后使用MATLAB的fsolve函数来求解方程。将求得的根代入原方程,如果结果接近0,说明求得的解是正确的。
源程序:
m = 83;
f = @(x, m) exp(x) - 3*m/(m+100)*x.^2;
df = @(x, m) exp(x) - 6*m/(m+100)*x;
% 绘制函数图像
x = linspace(-2, 2, 100);
y = f(x, m);
plot(x, y); grid;
xlabel('x'); ylabel('f(x)');
title('函数图像');
% 绘制导函数图像
dy = df(x, m);
figure;
plot(x, dy); grid;
xlabel('x');ylabel('f''(x)');
title('导函数图像');
x0 = fzero(@(x) f(x, m), 0)
check = f(x0,m) % 验证解
结果和答案:
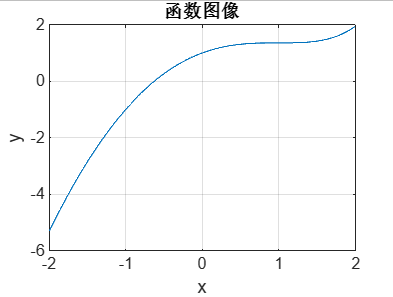

求出的根是-0.6267,代入原方程检查所得的值接近于0,说明求根正确。因为导函数单调递增,说明只存在一个根。
3
作出函数f(x)=ex−cosxf(x)=e^x-\cos xf(x)=ex−cosx的图形;求出方程f(x)=0f(x)=0f(x)=0的所有根;令xnx_nxn为从 0 向左依次排列的方程的根,输出xn−1−xnx_{n-1}-x_nxn−1−xn,并指出limn→∞(xn−1−xn)=?.\lim_n\to\infty(x_{n-1}-x_n)=?.limn→∞(xn−1−xn)=?.
解题分析:
先定义方程,并画出其图像。由于此方程可能存在多个根,所以要在不同的初始估计值上运行 fzero 函数来找到所有的根。我们可以通过观察图形来选择这些初始估计值。将找到的所有根排序,然后计算相邻根之间的差值。最后通过这些差值来得到极限。
源程序:
% 定义函数
f = @(x) exp(x) - cos(x);
% 定义x的范围
x = linspace(-10, 10, 1000);
% 计算对应的y值
y = f(x);
% 画图
figure
plot(x, y)
xlabel('x')
ylabel('f(x)')
grid on
% 初始化根的数组
roots = [];
% 在不同的初始估计值上运行fzero函数
for x0 = -10:10
try
root = fzero(f, x0);
% 只有当找到的根不在roots数组中时,才将其添加到roots数组中
if isempty(roots) || min(abs(roots - root)) > 1e-6
roots = [roots, root];
end
catch
% 忽略无法找到根的情况
end
end
% 将找到的所有根排序
roots = sort(roots);
% 计算相邻根之间的差值
differences = diff(roots);
% 输出相邻根之间的差值
disp('相邻根之间的差值:')
disp(differences)
% 估计极限
limit = differences(end);
disp('极限为:')
disp(limit)
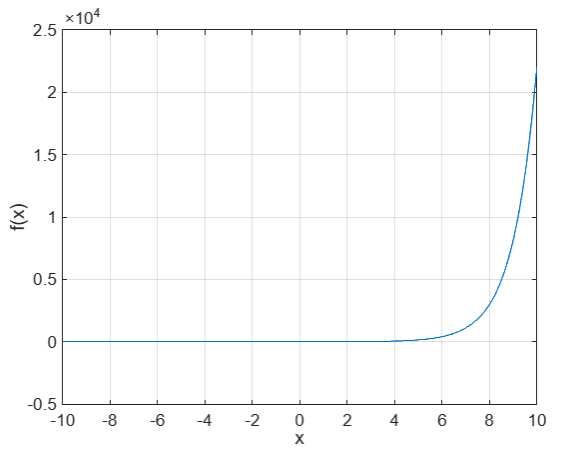
结果和答案:

4
求两个平面曲线x2−y2+sinx+2y=1x^2-y^2+\sin x+2y=1x2−y2+sinx+2y=1与x2+3y2+xy−y=5x^2+3y^2+xy-y=5x2+3y2+xy−y=5的交点。
解题分析:
可以视为一个两条曲线所并联的非线性方程组的求解问题,使用MATLAB的fsolve函数来求解。
源程序:
% 定义非线性方程组
f = @(x) [x(1)^2 - x(2)^2 + sin(x(1)) + 2*x(2) - 1;
x(1)^2 + 3*x(2)^2 + x(1)*x(2) - x(2) - 5];
% 使用fsolve函数求解非线性方程组
solution1 = fsolve(f, [-1.7,-0.4]);
solution2 = fsolve(f, [-1,1.5]);
solution3 = fsolve(f, [0.1,1.4]);
solution4 = fsolve(f, [1.7,-1]);
solution1,solution2,solution3,solution4
结果和答案:

5
分析函数f(x)=x2(x−1)2+x+1−x(x−3)2+x+1f(x)=\frac{x^{2}}{(x-1)^{2}+x+1}-\frac{x}{(x-3)^{2}+x+1}f(x)=(x−1)2+x+1x2−(x−3)2+x+1x, 给出它的极值和单调区间
解题思路:
先定义函数f(x)f(x)f(x)并求导。然后,求解f′(x)=0f'(x)=0f′(x)=0的解,这些解代表函数可能的极值点。检查它们的符号以确定它们是极值类型和单调区间。
源代码
syms x
f = (x^2)/((x-1)^2 + x + 1) - x/((x-3)^2 + x + 1);
df = diff(f, x); % 计算导数
p = solve(df, x); % 找到导数为0的点
p = double(p);p_real = p(imag(p)==0);
critical_points = unique(p_real); % 去除重复值
ddf = diff(df, x); % 计算二阶导数
second_derivative_values = double( ...
subs(ddf, x, critical_points));
figure;
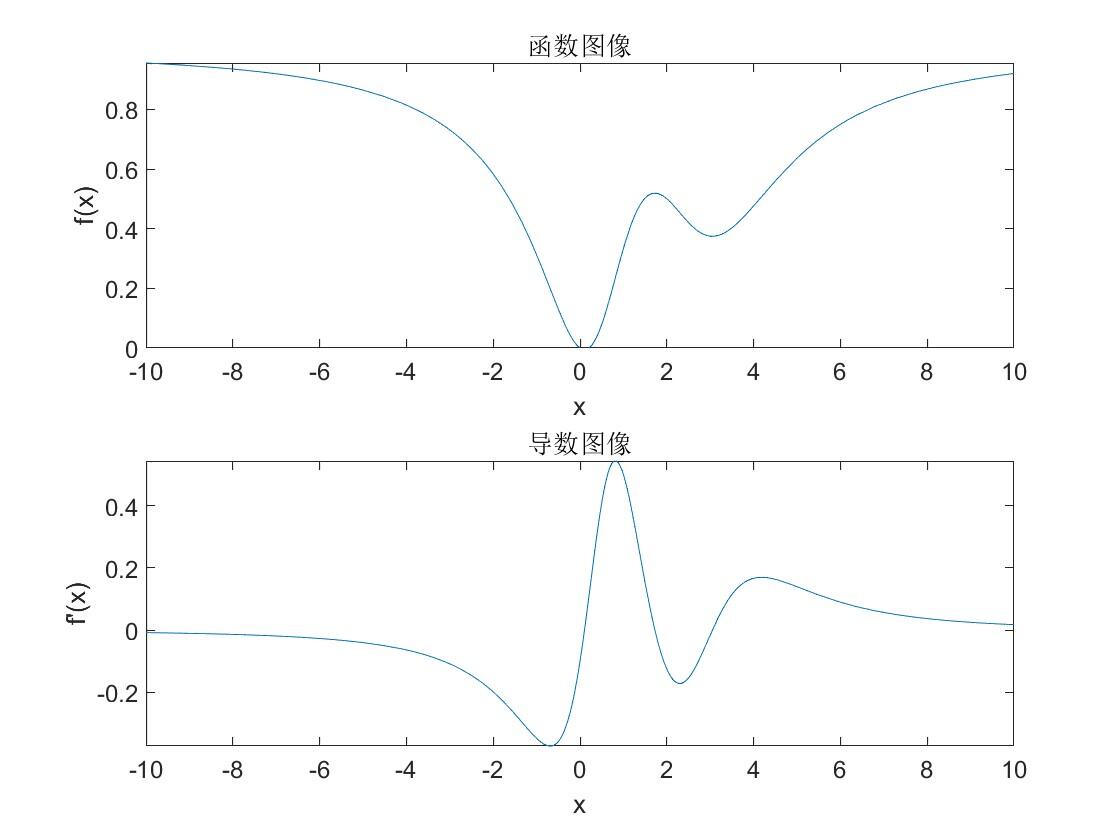
subplot(2,1,1);fplot(f, [-10, 10])
title('函数图像');
xlabel('x');ylabel('f(x)');
subplot(2,1,2);fplot(df, [-10, 10])
title('导数图像');xlabel('x');ylabel('f''(x)')
结果和答案:
x=0.103473 是极小值点
x=1.725482 是极大值点
x=3.049763 是极小值点
在区间(-Inf,0.103473)上,函数是减函数
在区间(0.103473,1.725482)上,函数是增函数
在区间(1.725482,3.049763)上,函数是减函数
在区间(3.049763,Inf)上,函数是增函数
6
农夫老李有一个半径为 10m 的圆形牛栏,里面长满了草,老李要将家里的一头牛拴在牛栏边的一根栏桩上,要求只让牛吃到圆形牛栏中的一半的草,请问栓牛鼻的绳子应为多长?
解题思路:
扇形的面积应该等于圆形牛栏面积的一半。可以使用数值方法来求解这个问题。然后遍历每个半径值对应的扇形面积,然后找出和圆形牛栏面积的一半最接近的的半径值,这个半径值就是牛应该被拴的绳子的长度。
源代码:
r = 10:0.001:10*sqrt(2);
x1 = (r.*sqrt(4 - r.^2/100))/2;
x2 = -(r.*sqrt(4 - r.^2/100))/2;
area=@(x,c)(c^2-x.^2).^(1/2)-10+(100-x.^2).^(1/2);
% 定义你的两个函数
f1 = @(i) integral(@(x)area(x,r(i)),x2(i),x1(i));
f2 = @(r) pi*100/2*r./r;
% 计算两个函数在所有 r 值上的值
f1_values = arrayfun(f1, 1:length(r));
f2_values = f2(r);
% 找到等于0的点
[~, i] = min(abs(f1_values - f2_values));
r(i)
结果和答案:

7
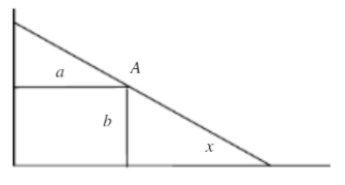
要运送一根细杆通过由直径为 5cm 和直径为 10cm 组成的垂直圆形通道(如图),问细杆最长是多少?

解题思路:
要找到一个角度,使得细杆能够通过两个垂直圆形通道,且细杆的长度尽可能长。
设变量 ttt 表示细杆与水平面的夹角。
然后,将问题转化为一个数学优化问题。这个优化问题的目标函数为 f=5/sin(t)+10/cos(t)f=5/\sin(t)+10/\cos(t)f=5/sin(t)+10/cos(t),这个函数表示细杆的长度。其中在这个函数中,5/sin(t)5/\sin(t)5/sin(t) 表示细杆在小的通道中的长度,10/cos(t)10/\cos(t)10/cos(t) 表示细杆在大的通道中的长度。
最后用 fminsearch 函数来找到使得 fff 最小的 ttt 值。
源代码:
%取初始值pi/4, 计算如下
fun=@(t)5/sin(t)+10/cos(t);
[t,f]=fminsearch(fun, pi/4)
结果和答案:

8
(综合实验) 一幢楼房的后面是一个很大的花园。在花园中仅靠着楼房有一个温室, 温室伸入花园宽 2m,高 3m,温室正上方是楼房的窗台。清洁工打扫窗台周围,他得用梯子越过温室,一头放在花园中,一头靠在楼房的墙上。因为温室是不能承受梯子压力的,所以梯子不能太短。现清洁工只有一架 7m 长的梯子,你认为它能达到要求吗?能满足要求的梯子的最小长度为多少?
[实验目的]
掌握求一元函数极值、最值的计算方法,并会用它解决一些实际问题;掌握 Matlab 求极小值的命令 fminbnd。
[实验要求]
1、设温室宽为 a,高为 b,梯子倾斜的角度为 x,当梯子与温室顶端恰好接触时,梯子的
长度 L 只与 x 有关,是写出函数 L(x)及定义域。
2、将 a、b 赋值,画出 L(x)的图形,注意自变量 x 的范围选取。
3、利用极值定义并结合极值的判定条件求极小值。
4、用驻点法求极小值。
5、直接用求极小值求极小值的命令求解,与上面两个结果比较。
6、任意改变 a、b 的取值,重新运行程序,即可得相应结果。
7、取 a=1.8,在只用 6.5m 长梯子的情况下,温室最多能修建多高?
解题思路:
-
设定以下符号:LLL:梯子的长度;L1L_1L1:梯子的上半段;L2L_2L2:梯子的下半段;xxx:梯子与地面的夹角。
易知:L=L1+L2L = L_1 + L_2L=L1+L2 ,则梯子的长度LLL与角度xxx的关系可以表示为:L(x)=acos(x)+bsin(x)L(x) = \frac{a}{\cos(x)} + \frac{b}{\sin(x)}L(x)=cos(x)a+sin(x)b。这个函数的定义域是0<x<π20 < x < \frac{\pi}{2}0<x<2π。 -
画出L(x)L(x)L(x)的图形的源代码:
a=2;b=3; f= @(x) a/cos(x) + b/sin(x); fplot(f,[0 pi/2+0.01])
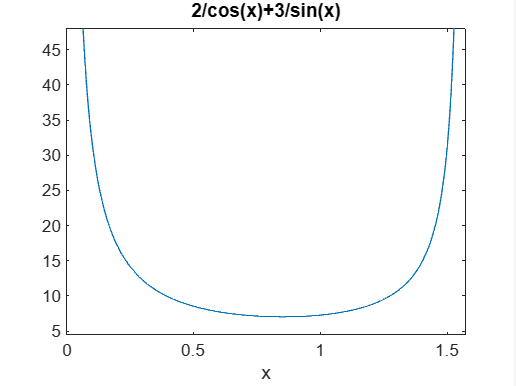
-
利用极值定义并结合极值的判定条件求极小值。首先,我们需要求出L(x)L(x)L(x)的一阶导数和二阶导数然后,我们需要找到一阶导数为0的点,这可以通过求解方程f′(x)=0f'(x) = 0f′(x)=0来完成。最后,我们需要通过二阶导数测试来确定这些点是否为极小值:
syms x; % 定义变量 a=2;b=3; % 温室的高度和宽度 L = a/cos(x) + b/sin(x); % 梯子的长度公式 dL = diff(L, x); % 求导数 % 求解导数等于零的点 x_min = fzero(matlabFunction(dL),0.75); % 计算梯子的最小长度 L_min = subs(L, x, x_min); disp(['梯子的最小长度为:', num2str(double(L_min)), ' 米']) if (L_min > 7) disp('梯子长度不能达到要求') end结果和答案:

-
用驻点法求极小值,源代码:
syms x; % 定义变量 a=2;b=3; % 温室的高度和宽度 L = a/cos(x) + b/sin(x); % 梯子的长度公式 dL = diff(L, x); % 求导数 % 求解导数等于零的点 x_min = fzero(matlabFunction(dL),0.75); % 求二阶导数 ddL = diff(dL, x); % 判断极值 if subs(ddL, x, x_min) > 0 L_min = subs(L, x, x_min); disp(['梯子的最小长度为:', num2str(double(L_min)), ' 米']) else disp('没有找到极小值') end if (L_min > 7) disp('梯子长度不能达到要求') end结果和答案:

-
直接用求极小值求极小值的命令求解:
a = 2;b = 3; f = @(x) a./cos(x) + b./sin(x); [x,fval] = fminbnd(f,0,pi/2) if (fval > 7) disp('梯子长度不能达到要求') end结果和答案:

-
任若设置a=1.5a=1.5a=1.5,b=2.5b=2.5b=2.5,然后重复上述步骤,运行结果
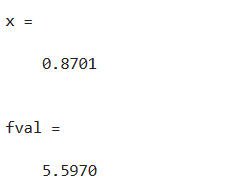
-
分析题意,需要我们解出当L(x)=6.5L(x) = 6.5L(x)=6.5时的bbb值:
a = 1.8; fun = @(b,x) a./cos(x) + b./sin(x); x = linspace(0, pi/2, 1000); % 生成一个从0到pi/2的数列 b = linspace(0, 10, 1000); % 假设b的可能值在0到10之间 [B, X] = meshgrid(b, x); % 生成一个网格 Z = fun(B, X); % 计算函数值 % 找到最接近6.5的Z值的位置 [~, idx] = min(abs(Z - 6.5), [], 'all', 'linear'); % 找到对应的b值 b_max = B(idx) disp(['在只用6.5m长梯子的情况下,温室最多能修建的高度为: ', num2str(max_height), 'm']);结果和答案:

模块三 选代法
教学要求:了解函数迭代的概念,会用迭代法求非线性方程的根,会用 MTALAB 软件编程画迭代的“蜘蛛网”图、散点图,讨论迭代的收敛性;会用 MTALAB 软件编程画迭代的“蜘蛛网”图、散点图;了解特征值、特征向量与线性迭代的关系,并会利用线性迭代解决实际问题。
1
用 2 分法和黄金分割法(选择黄金分割点)求方程x+x2+1−11e−x2=0x+\sqrt{x^2+1}-11e^{-x^2}=0x+x2+1−11e−x2=0的根(误差不超过10−710^{-7}10−7),给出两种方法的迭代散点图(横轴为迭代次数,纵轴为对应的近似根。画在同一坐标系内),指出它们的收敛特性。
解题思路:
-
二分法:二分法是一种求解一元方程近似根的方法。其基本思想是:在方程连续、单调的定义域内,通过不断地把函数解的存在区间一分为二,使区间的长度趋近于0,从而得到方程近似解的一种方法。
-
黄金分割法:利用黄金分割比例(约为0.618)来进行搜索,从而达到快速搜索的目的。
源代码:
% 定义函数
f = @(x) x + sqrt(x.^2 + 1) - 11*exp(-x.^2);
% 画出函数图像
x = linspace(-3, 2, 1000);
y = f(x);
figure;
plot(x, y);
xlabel('x');
ylabel('y');
title('函数图像');
grid on;
% 定义二分法和黄金分割法
function [root, history] = bisection(f, a, b, tol, split)
history = [];
if nargin < 5
split = 0.5; % 默认分割点是中间
end
while abs(b-a) > tol
c = a + split*(b - a);
history = [history; c];
if f(c) == 0
root = c;
return;
elseif f(a)*f(c) < 0
b = c;
else
a = c;
end
end
root = a + split*(b - a);
end
% 求解
tol = 1e-7;
[root1, history1] = bisection(f, -3, -1, tol);
[root2, history2] = bisection(f, 0, 2, tol);
phi = (sqrt(5)-1)/2;
[root3, history3] = bisection(f, -3, -1, tol, phi);
[root4, history4] = bisection(f, 0, 2, tol, phi);
% 输出迭代次数和最终结果
disp('迭代次数和最终结果:');
disp(['二分法(-3,-1): 迭代次数 = ', num2str(length(history1)), ', 近似根 = ', num2str(root1)]);
disp(['黄金分割法(-3,-1): 迭代次数 = ', num2str(length(history3)), ', 近似根 = ', num2str(root3)]);
disp(['二分法(0,2): 迭代次数 = ', num2str(length(history2)), ', 近似根 = ', num2str(root2)]);
disp(['黄金分割法(0,2): 迭代次数 = ', num2str(length(history4)), ', 近似根 = ', num2str(root4)]);
% 画出迭代过程
figure;
plot(1:length(history1), history1, 'r');
hold on;
plot(1:length(history2), history2, 'b');
plot(1:length(history3), history3, 'g');
plot(1:length(history4), history4, 'k');
xlabel('迭代次数');
ylabel('近似根');
title('迭代过程');
legend('二分法(-3,-1)', '二分法(0,2)', '黄金分割法(-3,-1)', '黄金分割法(0,2)','Location','east');
grid on;
结果和答案:


收敛特性:两种分割法确定的初始点会不同。二分法的收敛速度是线性的,每次迭代后,误差大约减半。而黄金分割法的收敛速度更快。
2
任取初值x0x_0x0,讨论函数f(x)=ax(1−x)f(x)=ax(1-x)f(x)=ax(1−x)在a=2.85, 3.4, 3.6, 3.75时作迭代产生的迭代数列的收敛、周期或混沌特征。(取n=300n=300n=300,分别对不同 a 值画出(n,xn)(n,x_n)(n,xn)的散点图进行观察)
解题分析:
在每次迭代使用上一次的结果xnx_nxn作为新的输入,得到新的结果xn+1=f(xn)x_{n+1}=f(x_n)xn+1=f(xn)。然后,观察这个过程:xnx_nxn是否收敛(即是否稳定在一个值),是否有周期性(即是否在一组值之间循环),或者是否显示混沌特性(即看似随机,但又有确定的规律)。
源程序:
% 定义参数
a_values = [2.85, 3.4, 3.6, 3.75]; % a的取值
x0 = 0.5; % 初始值
n = 300; % 迭代次数
% 初始化图形
figure;
% 对每个a值进行迭代
for i = 1:length(a_values)
a = a_values(i);
x = zeros(1, n); % 初始化x
x(1) = x0; % 设置初始值
% 迭代
for j = 2:n
x(j) = a * x(j-1) * (1 - x(j-1));
end
% 在子图中绘制散点图
subplot(2, 2, i);
plot(1:n, x, '.');
title(['a = ', num2str(a)]);
xlabel('n');
ylabel('x_n');
end
结果和答案:

a=2.85时,迭代数列有收敛,无周期,系统的稳定点大约是0.649,所有的初始值x0∈[0,1]x_0 \in [0, 1]x0∈[0,1]都将收敛到该点。
a=3.4时,迭代数列存在周期,该混沌系统存在两个稳定点,系统会在这两个点之间循环。
a=3.6时,迭代数列无收敛,存在周期,该混沌系统存在四个稳定点,系统会在这四个点之间循环。
a=3.75时,迭代数列处于混沌状态,经过多次迭代后,x的值将在一多个区间内跳跃,而这些区间的位置和宽度都是不规则的。
3
(人口流动趋势)对城乡人口流动作年度调查,发现有一个稳定的向城镇流动的趋势, 每年农村居民的 5%移居城镇而城镇居民的 1%迁出.现在总人口的 20%位于城镇.假如城乡总人口保持不变,并且人口流动的这种趋势继续下去.
(1)一年以后城镇人口所占比例是多少?两年以后呢?十年以后呢?
(2)很多年以后呢?
(3)如果现在总人口的 70%位于城镇,问很多年以后城镇人口所占比例是多少?
(4)计算转移矩阵的最大特征值及对应的特征向量,与问题(2)、(3)有何关系?
解题分析:
先定义转移矩阵T和初始人口分布P。然后,通过多次矩阵乘法计算得到不同年份后的人口分布。通过计算城镇人口在总人口中的比例,可以得到每个问题的答案。
源代码:
% (1) 一年以后城镇人口所占比例
T = [0.99 0.05; 0.01 0.95]; % 转移矩阵
P = [0.2; 0.8]; % 初始人口分布,城镇人口占比为20%
P_one_year = T * P; % 一年后人口分布
town_ratio_one_year = P_one_year(1) / sum(P_one_year);
fprintf('一年后城镇人口所占比例:%.2f\n', town_ratio_one_year);
% (2) 两年以后城镇人口所占比例
P_two_years = T * P_one_year; % 两年后人口分布
town_ratio_two_years = P_two_years(1) / sum(P_two_years);
fprintf('两年后城镇人口所占比例:%.2f\n', town_ratio_two_years);
% (3) 十年以后城镇人口所占比例
P_ten_years = T^10 * P; % 十年后人口分布
town_ratio_ten_years = P_ten_years(1) / sum(P_ten_years);
fprintf('十年后城镇人口所占比例:%.2f\n', town_ratio_ten_years);
% (4) 计算转移矩阵的最大特征值及对应的特征向量
[V, D] = eig(T); % T的特征向量矩阵V,特征值矩阵D
max_eigenvalue = max(diag(D)); % 转移矩阵的最大特征值
max_eigenvalue_vector = V(:, find(diag(D) == max_eigenvalue)); % 对应的特征向量
fprintf('转移矩阵的最大特征值:%.4f\n', max_eigenvalue);
fprintf('对应的特征向量:\n');
disp(max_eigenvalue_vector);
结果和答案:

(2)、(3)与最大特征值有关系
- 当转移矩阵的最大特征值小于1时,人口分布会趋向于稳定,城镇人口所占比例将收敛到一个固定值。
- 当转移矩阵的最大特征值等于1时,人口分布将保持不变,城镇人口所占比例也将保持不变。
- 当转移矩阵的最大特征值大于1时,人口分布会发生周期性波动,城镇人口所占比例将在波动中变化。
4
设x1=1,x2=2x_1=1,x_2=2x1=1,x2=2,对n≥1,xn+1=xn+xn−1n\geq1,x_{n+1}=x_n+x_{n-1}n≥1,xn+1=xn+xn−1。利用符号矩阵特征分解给出序列{xn}\{x_n\}{xn}的通项。(利用线性迭代类似思想求通项)
解题思路:
这个问题是一个线性递推问题,可以通过构造转移矩阵和初始向量,然后使用矩阵的特征值和特征向量来找到这个序列的通项公式。先构建线性递推关系的转移矩阵。
设斐波那契数列第n项为FnF_nFn,向量uk=[Fk+1Fk]\boldsymbol{u}_k=\begin{bmatrix}F_{k+1}\\F_k\end{bmatrix}uk=[Fk+1Fk],则u0=[F1F0]=[10]\boldsymbol{u}_0=\begin{bmatrix}F_1\\F_0\end{bmatrix}=\begin{bmatrix}1\\0\end{bmatrix}u0=[F1F0]=[10],由于{Fk+2=Fk+1+FkFk+1=Fk+1\left.\left\{\begin{array}{l}F_{k+2}=F_{k+1}+F_k\\F_{k+1}=F_{k+1}\end{array}\right.\right.{Fk+2=Fk+1+FkFk+1=Fk+1,因而uk+1=[1110][Fk+1Fk]=[1110]uk\boldsymbol{u}_{k+1}=\begin{bmatrix}1&1\\1&0\end{bmatrix}\begin{bmatrix}F_{k+1}\\F_k\end{bmatrix}=\begin{bmatrix}1&1\\1&0\end{bmatrix}\boldsymbol{u}_kuk+1=[1110][Fk+1Fk]=[1110]uk
然后,找到这个矩阵的特征值和特征向量。最后,使用这些特征值和特征向量来构建通项公式。
源代码:
A = [sym(1) sym(1); sym(1) 0];
% 计算矩阵的特征值和特征向量
[V, D] = eig(A);
disp('特征值:');
disp(D);
disp('特征向量:');
disp(V);
x0 = [sym(2); sym(1)]; % 初始值
% 使用特征值和特征向量来构建通项公式
syms n
x_n = V * (D^n) * inv(V) * x0;
% 简化表达式
x_n = simplify(x_n);
% 输出通项公式
disp('通项公式:');
disp(x_n(2));
结果和答案:

5
(综合实验)[比赛名次问题]
六名选手 A、B、C、D、E 和 F 进行围棋单循环
比赛,其比赛结果如下:
A 战胜 B、D、E、F;
B战胜 D、E、F;
C战胜 A、B、D;
D 战胜 E、F;
E 战胜 C、F;
F 战胜 C.
请你给六名选手排一个合理的名次.(写清建模过程)
解题思路:
如果按照每战胜一名选手得一分的原则,初步确定选手的名次,那么根据题目的已知信息,可以得到得分向量 s0=(4,3,3,2,2,1)Ts_0=(4,3,3,2,2,1)^Ts0=(4,3,3,2,2,1)T。然而,这种方法并不完全合理,题目中出现了并列名次,所以应该改变计分机制,使分数不同,从而分出名次。
为了解决这个问题,我们可以根据得分向量 s0s_0s0 判定选手的强弱,然后重新计算得分。如计分机制改为,该选手所赢过的所有对手在s0s_0s0中所对应的得分之和,则A的得分为3+2+2+1=8,以此类推,我们可以得到修正后的得分向量 s1=(8,5,9,3,4,3)Ts_1=(8,5,9,3,4,3)^Ts1=(8,5,9,3,4,3)T。但是如果我们更换排名的根据,如根据s1s_1s1再算一次,则此刻的得分向量 s2=(15,10,16,7,12,9)Ts_2=(15,10,16,7,12,9)^Ts2=(15,10,16,7,12,9)T。可以观察到,因为评分根据的不同,名次可能会出现波动现象。我们继续计算得分向量 sks_ksk,计算 s3,s4,…s_3,s_4, \ldotss3,s4,… 直到观察到得分向量的极限是否存在。
将选手的成绩表示为矩阵 MMM,其中的元素表示选手之间的胜负关系。通过迭代矩阵乘法,我们可以得到 sk=Msks_k=M_{s_{k}}sk=Msk。我们可以编写程序来计算 sks_ksk,并观察其极限是否存在。
为了确定选手的最终名次,我们可以使用归一化迭代的方法,将得分向量的各分量除以一个正数,以得到归一化的得分向量。根据归一化迭代方法,序列将收敛于迭代矩阵的最大特征值对应的特征向量。因此,我们可以使用迭代矩阵的最大特征值对应的特征向量来确定选手的名次。
源代码:
% 定义矩阵M
M = [0 1 0 1 1 1;
0 0 0 1 1 1;
1 1 0 1 0 0;
0 0 0 0 1 1;
0 0 1 0 0 1;
0 0 1 0 0 0];
s = ones(6, 1); % 初始化得分向量s
% 进行归一化迭代
for k = 1:1000
s_next = M * s; % 计算新的得分
% 对新的得分进行归一化
s_next = s_next / norm(s_next);
% 检查是否收敛,如果收敛则退出循环
if norm(s_next - s) < 1e-6
break;
end
% 更新得分
s = s_next;
end
% 打印最终排名
[sorted_scores, sorted_indices] = sort(s, 'descend');
players = ['A', 'B', 'C', 'D', 'E', 'F'];
for i = 1:6
fprintf('第%d名: 选手%s,得分:%.4f\n', i, players(sorted_indices(i)), sorted_scores(i));
end
结果和答案:

模块四:数据建模与综合实验
教学要求:掌握插值和拟合的基本思想,了解最小二乘法的本质,掌握线性最小二乘和非线性最小二乘的求解方法,并能够利用 MATLAB 相关函数求解线性和非线性最小二乘问题,掌握数据建模的一般步骤。
1
在 n个人的团体中,如果不考虑年龄的差异,研究是否有两个或两个以上的人生日相同。假设每人的生日在一年 365 天中的任意一天式等可能人)。这 n 个人生日各不相同的概率为P(n)=P365n365n=365(365−1)⋯(365−n+1)365nP(n)=\frac{P_{365}^{n}}{365^{n}}=\frac{365(365-1)\cdots(365-n+1)}{365^{n}}P(n)=365nP365n=365n365(365−1)⋯(365−n+1)。
(1)计算出当团体人数取 n=1,2,…100 时概率值 P(1), P(2),…, P(100), 并绘制图形,描述概率值随团体人数变化的规律;
(2)用计算机模拟的方法计算 n个人生日各不相同的频率 f(n),并比较概率 p(n)与频率 f(n)之间的差异;
(3)利用数学分析的方法给出 P(n)的近似计算方法,并对不同的 n,比较 P(n)与近似值之间的差异;
问题分析:
(1)题目中给出了公式P(n)=P365n365n=365(365−1)⋯(365−n+1)365nP(n)=\frac{P_{365}^{n}}{365^{n}}=\frac{365(365-1)\cdots(365-n+1)}{365^{n}}P(n)=365nP365n=365n365(365−1)⋯(365−n+1)来计算。
源代码:
P = zeros(1, 100); % 存储概率值
n = 1:100; % 人数
% 计算概率
for i = 1:100
P(i) = prod((365 - (0:i-1)) / 365);
end
figure; % 绘图
plot(n, P);xlabel('人数'); ylabel('生日各不相同的概率');
title('概率值随团体人数变化的规律');
结果和答案:
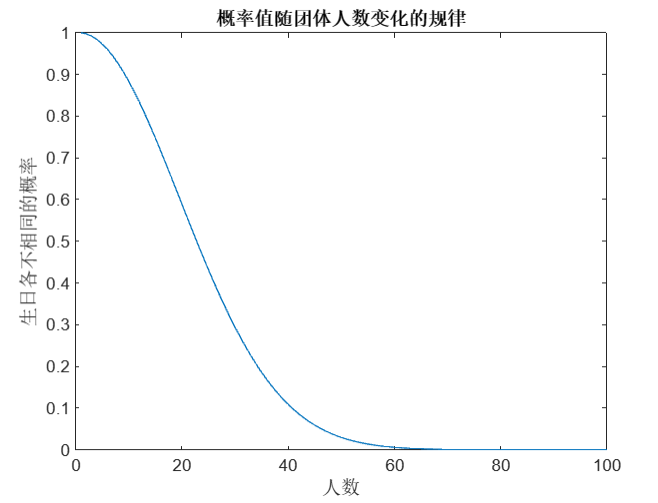
(2)用计算机模拟的方法计算 n个人生日各不相同的频率 f(n),并比较概率 p(n)与频率 f(n)之间的差异:
源代码:
N = 10000; f = zeros(1, 100);
for i = 1:100
count = 0;
for j = 1:N
birthdays = randi(365, 1, i);
if length(unique(birthdays)) == i
count = count + 1;
end
end
f(i) = count / N;
end
figure; % 比较概率与频率
plot(n, P, 'r', n, f, 'b');
legend('概率', '频率'); xlabel('人数');
ylabel('生日各不相同的概率/频率');
title('概率与频率的比较');
结果和答案:
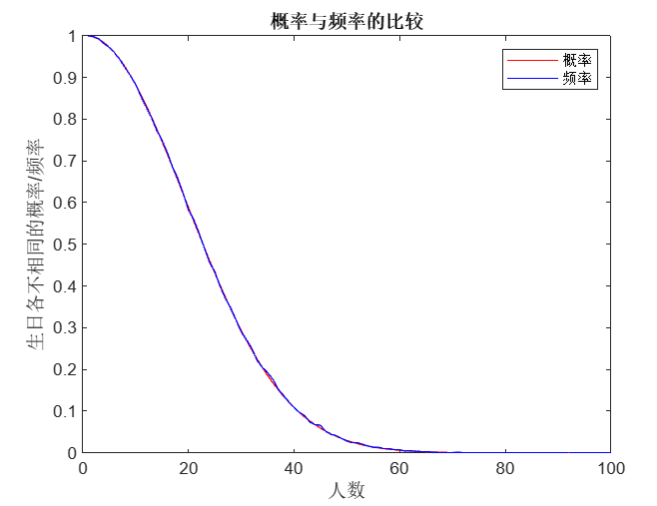
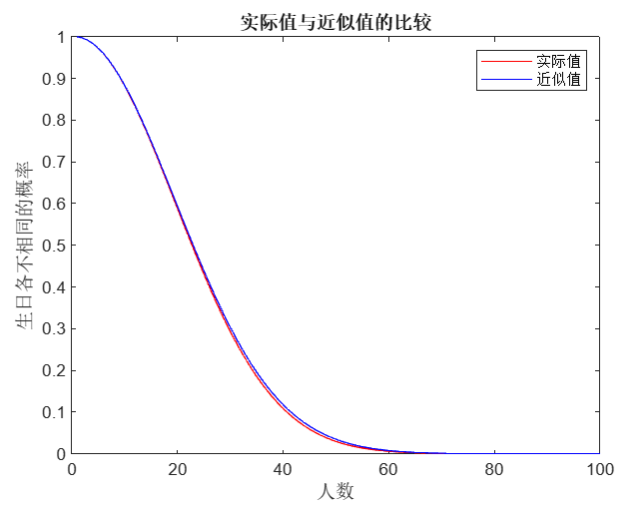
(3)利用数学分析的方法给出 P(n)的近似计算方法,并对不同的 n,比较 P(n)与近似值之间的差异:
近似计算方法可以使用泰勒级数的前两项来得到,即 P(n)≈e−n(n−1)/2∗365P(n) \approx e^{-n(n-1)/2*365}P(n)≈e−n(n−1)/2∗365。
% 计算近似值
P_approx = exp(-n.*(n-1)/2/365);
% 比较概率与近似值
figure;
plot(n, P, 'r', n, P_approx, 'b');
legend('实际值', '近似值');
xlabel('人数');
ylabel('生日各不相同的概率');
title('实际值与近似值的比较');
结果和答案:
2
根据最小二乘法,用 5 次多项式p(x)=a0+a1x+⋯+a5x5p(x)=a_0+a_1x+\cdots+a_5x^5p(x)=a0+a1x+⋯+a5x5表示下表中数据 x 和 y 间的关系,求对应最小二乘问题的法方程组(用矩阵和向量表示),并求解,计算误差平方和∑i−1m(a0+a1x+⋯+a5x5−yk)2\sum_{i-1}^{m}(a_{0}+a_{1}x+\cdots+a_{5}x^{5}-y_{k})^{2}∑i−1m(a0+a1x+⋯+a5x5−yk)2
| X | 0.11 | 0.25 | 0.3 | 0 | -1.2 | -0.33 | -2 | 1 | 2.3 |
|---|---|---|---|---|---|---|---|---|---|
| V | 0.85 | 1.22 | 0.5 | 1.03 | 1.55 | 0.44 | 0.8 | 2.3 | 3.5 |
解题思路:
在最小二乘法中,我们寻找一组参数(在这个问题中是多项式的系数a0,a1,...,a5a_0, a_1, ..., a_5a0,a1,...,a5),使得函数在给定的数据点上的预测值与实际值之间的差的平方和最小。这个差的平方和被称为残差平方和,记作RSSRSSRSS,在这个问题中,它的形式为:
RSS=∑i=1m(yi−(a0+a1xi+⋯+a5xi5))2RSS = \sum_{i=1}^{m}(y_i - (a_{0}+a_{1}x_i+\cdots+a_{5}x_i^{5}))^{2}RSS=i=1∑m(yi−(a0+a1xi+⋯+a5xi5))2
其中,xix_ixi和yiy_iyi是给定的数据点,mmm是数据点的数量。
为了找到最小化RSSRSSRSS的参数,我们需要计算RSSRSSRSS关于每个参数的偏导数,并将它们设为0,然后解出这个线性方程组。这就是所谓的法方程组。在这个问题中,法方程组可以写成矩阵形式Ax=bAx=bAx=b,其中AAA是一个6×66 \times 66×6的矩阵,bbb是一个6×16 \times 16×1的向量,它们的元素分别为:
Aij=∑k=1mxki+j−2,i,j=1,2,...,6A_{ij} = \sum_{k=1}^{m} x_k^{i+j-2}, \quad i,j = 1,2,...,6Aij=k=1∑mxki+j−2,i,j=1,2,...,6
bi=∑k=1mxki−1yk,i=1,2,...,6b_i = \sum_{k=1}^{m} x_k^{i-1}y_k, \quad i = 1,2,...,6bi=k=1∑mxki−1yk,i=1,2,...,6
求解这个线性方程组,我们就可以得到最小化RSSRSSRSS的参数a0,a1,...,a5a_0, a_1, ..., a_5a0,a1,...,a5。
源代码:
% 数据点
x = [0.11 0.25 0.3 0 -1.2 -0.33 -2 1 2.3];
y = [0.85 1.22 0.5 1.03 1.55 0.44 0.8 2.3 3.5];
% 构建矩阵A和向量b
A = zeros(6,6);b = zeros(6,1);
for i = 0:5
for j = 0:5
A(i+1,j+1) = sum(x.^(i+j));
end
b(i+1) = sum(x.^i .* y);
end
a = A\b; % 求解线性方程组
% 计算误差平方和
err = sum((polyval(flip(a), x) - y).^2);
% 输出结果
disp('多项式系数:');disp(a);
disp('误差平方和:');disp(err);
运行这段代码,可以得到以下结果:

因此,用 5 次多项式 p(x)=0.7081+0.6222x+1.2931x2−0.1732x3−0.2305x4+0.0478x5p(x)=0.7081+0.6222x+1.2931x^2-0.1732x^3-0.2305x^4+0.0478x^5p(x)=0.7081+0.6222x+1.2931x2−0.1732x3−0.2305x4+0.0478x5 可以最好地拟合给定的数据点,误差平方和为0.4841。
3
求解非线性规划问题:minf(x)=x12−4x1−8x21+15\min f(x)=x_1^2-4x_1-8x_{21}+15minf(x)=x12−4x1−8x21+15,
s.t.{−x12−x22≤−92x1+3x2≤2x1−x2≤5s.t.\begin{cases}-x_1^2-x_2^2\leq-9\\2x_1+3x_2\leq2\\x_1-x_2\leq5\end{cases}s.t.⎩⎨⎧−x12−x22≤−92x1+3x2≤2x1−x2≤5
思路分析:
先定义目标函数和约束条件。然后优化工具箱中的fmincon函数。fmincon函数可以用于求解带有约束条件的非线性优化问题。
源代码:
% 定义目标函数
fun = @(x) x(1)^2 - 4*x(1) - 8*x(1)*x(2) + 15;
% 定义非线性约束条件
nonlcon = @(x) deal([-(x(1)^2 + x(2)^2 + 9); 2*x(1) + 3*x(2) - 2; x(1) - x(2) - 5], []);
x0 = [0, 0]; % 定义初始点
% 调用fmincon函数求解
options = optimoptions('fmincon','Display','iter','Algorithm','interior-point');
[x,fval] = fmincon(fun,x0,[],[],[],[],[],[],nonlcon,options)
结果和答案:

4
已知某天的气温变化记录如下
| 时刻 t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 温度 T | 15 | 13 | 13 | 14 | 14 | 15 | 16 | 18 | 20 | 22 | 23 | 25 | 28 |
| 时刻 t | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
| 温度 T | 31 | 32 | 31 | 30 | 27 | 25 | 24 | 22 | 20 | 18 | 17 | 16 |
分别用模型函数f(t)=aeb(t−c)2f(t)=ae^{b(t-c)^2}f(t)=aeb(t−c)2 和 g(t)=rsin(π12t+θ)+cg(t)=r\sin(\frac{\pi}{12}t+\theta)+cg(t)=rsin(12πt+θ)+c拟合上述数据,用最小二乘法确定系数,并分析误差。(画图显示拟合效果)
解题思路:
首先用匿名函数定义两个模型函数。然后,用最小二乘法来确定这些函数的参数。最后,分析误差并绘制图形来显示拟合效果。
源代码:
% 初始化数据
t = [0:12 13:24]; % 时刻
T = [15 13 13 14 14 15 16 18 20 22 23 25 28 31 32 31 30 27 25 24 22 20 18 17 16]; % 温度
% 定义模型函数
f = @(b,t) b(1).*exp(b(2).*(t-b(3)).^2); % f(t)=ae^{b(t-c)^2}
g = @(r,t) r(1).*sin(pi/12.*t+r(2))+r(3); % g(t)=r\sin(\frac{\pi}{12}t+\theta)+c
% 使用最小二乘法确定参数
b = nlinfit(t,T,f,[1 0.01 1]); % 参数初始化为[1 0.01 1]
r = nlinfit(t,T,g,[1 0.01 1]); % 参数初始化为[1 0.01 1]
% 计算拟合值
T_fit_f = f(b,t);
T_fit_g = g(r,t);
% 计算误差
error_f = norm(T-T_fit_f);
error_g = norm(T-T_fit_g);
% 输出误差
disp(['模型f的误差: ', num2str(error_f)]);
disp(['模型g的误差: ', num2str(error_g)]);
% 打印拟合函数
disp(['模型f的拟合函数: T = ', num2str(b(1)), ' * exp(', num2str(b(2)), ' * (t - ', num2str(b(3)), ')^2)']);
disp(['模型g的拟合函数: T = ', num2str(r(1)), ' * sin(pi/12 * t + ', num2str(r(2)), ') + ', num2str(r(3))]);
% 绘制图形
figure;
plot(t,T,'ko'); % 原始数据
hold on;
plot(t,T_fit_f,'r-'); % 模型f的拟合结果
plot(t,T_fit_g,'b-'); % 模型g的拟合结果
legend('原始数据','模型f的拟合结果','模型g的拟合结果');
xlabel('时刻');
ylabel('温度');
title('模型拟合结果和原始数据');
结果和答案:


5
(工资问题)现有一个木工,一个电工和一个油漆工,三人相互同意彼此装修他们自己
的房子。在装修之前,他们达成了如下协议:
(1)每人总共工作 10 天(包括给自己家干活在内);
(2)每人的日工资根据一般的市价在 60—80 元之间;
(3)每人的日工资数应使得每人的总收入与总支出相等。下表是他们协商后制定出的工作天数的分配方案,如何计算出他们每人应得的工资?
| 天数 \ 工种 | 木工 | 电工 | 油漆工 |
|---|---|---|---|
| 在木工家的工作天数 | 2 | 1 | 6 |
| 在电工家的工作天数 | 4 | 5 | 1 |
| 在油漆工家的工作天数 | 4 | 4 | 3 |
解题分析:
根据题目要求,我们需要计算出每个工人应得的工资,使得每个人的总收入与总支出相等。我们可以使用矩阵来表示每个工人在不同工种家中的工作天数。同时,我们可以定义一个长度为3的向量来表示每个工人的总工作天数和总收入。然后可以计算每个工人的总工作天数和总收入,再根据总收入与总支出相等的条件,计算出每个工人的日工资。
源代码:
% 定义每个工人在不同工种家中的工作天数
workdays = [2, 1, 6;
4, 5, 1;
4, 4, 3];
% 初始化变量
num_workers = size(workdays, 1);
num_jobs = size(workdays, 2);
total_workdays = zeros(1, num_workers);
total_income = zeros(1, num_workers);
% 计算总工作天数和总收入
for i = 1:num_workers
total_workdays(i) = sum(workdays(i, :));
total_income(i) = sum(workdays(i, :) .* randi([60, 80], 1, num_jobs));
end
% 计算日工资
daily_wages = total_income ./ total_workdays;
% 输出结果
for i = 1:num_workers
fprintf('工人%d的日工资为:%.2f元\n', i, daily_wages(i));
end
结果示例:

综合练习
综合练习部分的实验报告可以用 word 写,打印后附在实验报告后
综合练习一
(买房问题)房价不断上涨,国家频频出台调控政策,住房已经成为与我们每个人息息相关的事情。以一对夫妻为例,调查某地的房价、贷款等情况,结合两人收入与家庭储蓄等情况,建立数学模型,设计合适的购房方案。
对上述问题写一篇数模小论文,文章框架:问题重述、问题分析说明、模型建立与求解、模型拓展与应用。
综合练习二
(新冠疫情预测) 搜集全球新冠疫情的数据,选择全球数据或者某一个国家的数据,研究数据的函数类型,并根据全球或者某一国家截止 2022 年 5 月底的数据,预测全球或者该国家感染的最终规模,判断全球或该国家的疫情和何时结束。
具体要求:
- 本题可以由不多于 3 位同学组成一个小组共同完成,查阅资料、搜集数据、编写程
序、上机实践、撰写实验过程和实验结果。 - 同一个小组的答案可以一致,需写出小组成员学号、姓名及分工
- 两个不同小组的答案不得雷同,否则两个小组同学的成绩均不及格
- 本题实验报告篇幅不能少于 1200 字
个人学习小结
写一篇 500 字左右的个人小结,谈谈学习数学实验课程的建议等。
通过学习数学实验课程和实践操作,我不仅加深了对数学理论知识的理解,而且锻炼了解决实际问题的能力。在实验中,我频繁使用 MATLAB 软件进行计算和模拟,这让我对软件的操作更加熟练,也使得复杂的数学问题变得更加直观易懂。特别是在处理极限、微分、积分以及级数问题时,我学会了如何将理论知识转化为具体的编程实践,这种转化能力对于理解数学概念至关重要。
在解决具体问题,如计算生日概率、进行工资分配方案的优化时,我意识到数学模型在现实世界中的应用价值。这些问题的解决过程不仅考验了我的逻辑思维能力,也提升了我的数据分析和处理能力。此外,通过小组合作,我学会了如何与他人沟通和协作,这对于培养团队精神和协作能力非常有帮助。而且完成数学实验课程作业和报告时,也鼓励我自主学习新的概念和技术。这种自我驱动的学习态度对我的个人和专业成长都是非常有益的。
然而,数学实验课程也存在一些可以改进的地方。例如,课程在智慧课堂中没有课堂回放。同时,增加一些关于如何撰写科研论文和报告的指导,也将对学生的学术写作能力大有裨益。
总体来说,数学实验课程极大地丰富了我的学习生活,提高了我的专业素养。我相信,这些经历和技能将对我的未来学术研究或职业生涯产生积极的影响。我期待在未来的学习中,能够将这些宝贵的经验应用到更广泛的领域中去。




















 1338
1338

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








