C#使用泛型实现排序二叉树

最新推荐文章于 2024-08-03 14:35:20 发布
原创 最新推荐文章于 2024-08-03 14:35:20 发布
· 1.3k 阅读 · 2 ·
版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#二叉树 #泛型 #数据结构 #算法

什么是二叉树？
用一张图直观表示：
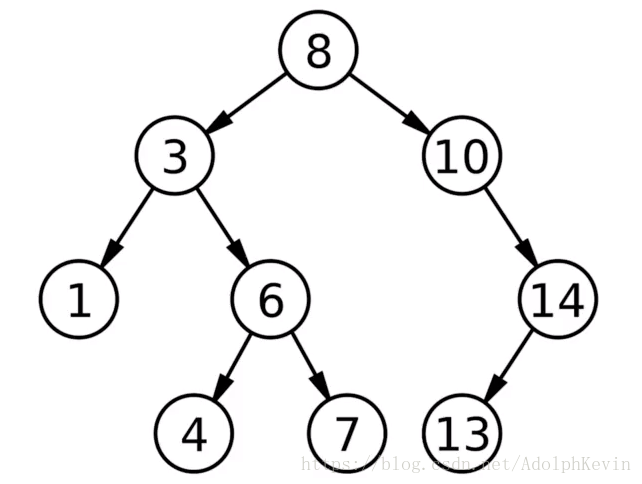
二叉树具有层级特效的数据结构。一棵树包含多个节点。
节点的层次属于二叉树的高，二叉树的效率衡量值由二叉树的高决定
排序二叉树（BST）特点：
    1、 左 子树上所有结点的值均 小于或等于 它的根结点的值
    2、 右 子树上所有结点的值均 大于或等于 它的根结点的值。
    3、 左、右子树也分别为二叉排序树。
顶部的节点称之为： 根节点，没有子树的节点称之为： 叶子节点

定义一个二叉树--C#实现：
采用泛型，适应性更广
public class Tree < TItem > where TItem : IComparable < TItem >
{
    private TItem NodeDate;//根节点
    private Tree< TItem > Left; //左子节点
    private Tree< TItem > Right; //右子节点
    /// <summary>
    /// 构造函数对树的对象复制
    /// </summary>
    /// <param name=" nodeValue "></param>
    public Tree( TItem nodeValue)
    {
        this .NodeDate = nodeValue;
        this .Right = null ;
        this .Left = null ;
    }
}
二叉树的 插入 ：
原理：插入值与根节点做比较，若插入值大于根节点，则插入至根节点的右子树，若插入值小于根节点，则插入至左子树
C#代码实现：
/// <summary>
/// 树的插入操作，实现二叉排序树
/// </summary>
/// <param name=" newItem "></param>
public void Insert( TItem newItem)
{
    TItem currentNodeValue = this .NodeDate;
    //当currentNodeValue>newItem 即当前节点大于等于当前数值
    {
        //若当前左子树为空
        if ( this .Left == null )
        {
            //则当前左子树作为新的根节点
            this .Left = new Tree< TItem >(newItem);
        }
        else //否则继续判断
        {
            this .Left.Insert(newItem);
        }
    }
    else //根节点小于当前数值
    {
        if ( this .Right == null )
        {
            this .Right = new Tree< TItem >(newItem);
        }
        else
        {
            this .Right.Insert(newItem);
        }
    }
}


常见的 二叉树遍历 --原理：
1、中序遍历：
    访问顺序：首先访问左子树，然后访问根节点，最后访问右子树。
    实现逻辑：如果当前左子树不为空，则继续访问左子树，直到左子树的叶子节点，打印当前叶子节点，再打印其根节点，再访问其根节点的右子节点。
    适用：将数值从小到大排序
2、前序遍历：首先访问根节点，再访问左子树，最后访问右子树。
    适用：当已有一个二叉树的时候，需要将已有二叉树复制一份时，前序遍历效果最好。比重新构建二叉树的效率高了10倍左右
3、后序遍历：首先访问左子树，再访问右子树，最后访问根节点。
    适用：举例：操作系统的文件遍历时，若当前根节点存在子树，则代表存在子文件夹，若无子树，则代表当前文件夹为最后一个文件夹，即可访问当前文件夹内的内容
4、层序遍历
5、z-型层序遍历
（4、5在此不做讨论）
一、中序遍历--C#代码实现：
从根节点开始->左子树->右子树
public void TraverseTreeInOrder()
{
    //如果当前左子树不为空
    if ( this .Left != null )
    {
        //则继续查找左子树
        this .Left.TraverseTreeInOrder();
    }
    //当没有左子树时，打印当前根节点
    Console.WriteLine(this.NodeDate);
    //如果当前右子树不为空
    if ( this .Right != null )
    {
        //继续遍历右子树
        this .Right.TraverseTreeInOrder();
    }
}

二、前序遍历--C#代码实现：
从根节点开始->左子树->右子树
public void TraverseTreePerOrder()
{
    Console.WriteLine(this.NodeDate);
    if ( this .Left != null )
    {
        this .Left.TraverseTreePerOrder();
    }
    if ( this .Right != null )
    {
        this .Right.TraverseTreePerOrder();
    }
}

三、后续遍历--C#代码实现：
从左子树开始->右子树->根节点
public void TraverseTreeLastOrder()
{
    if ( this .Left != null )
    {
        this .Left.TraverseTreeLastOrder();
    }
    if ( this .Right != null )
    {
        this .Right.TraverseTreeLastOrder();
    }
    Console.WriteLine(this.NodeDate);
}


二叉树的 查找 ：
原理：先判断当前节点是否存在，若存在，则用根节点与查找值左比较，若大于查找值，则进入左子树查询，若小于查找值，则进入右子树查找。存在则返回true，不存在则返回false
C#代码实现：
public bool TreeQuery(Tree< TItem > tree, TItem item)
{
    //如果当前节点为null，则代表不存在该数值
    if (tree == null )
    {
        return false ;
    }
    //如果NodeDate>item 当前节点大于当前数值
    if ( this . NodeDate.CompareTo(item ) > 0)
    {
        return TreeQuery(tree.Left, item);
    }//如果当前节点小于当前数值，则进入右子树查找
    else if ( this . NodeDate.CompareTo(item ) < 0)
    {
        return TreeQuery(tree.Right, item);
    }
    else
    {
        return true ;
    }
}

查找二叉树的最大值：
原理：二叉树的最大值位置在排序二叉树最右侧的节点。
先判断是当前节点是否存在，再判断当前节点是否存在右子树，若存在则进入右子树查询，一直访问至无右子树的节点，并返回此时（无右子树）的节点
C#代码实现：
public TItem TreeQueryMax(Tree<TItem> tree)
{
    if (tree != null )
    {
        while (tree != null && tree.Right != null )
        {
            tree = tree.Right;
        }
        return tree.NodeDate;
    }
    return default (TItem);
}

查找二叉树的最小值：
原理：二叉树的最小值位于排序二叉树的最左侧的节点。
先判断是当前节点是否存在，再判断当前节点是否存在左子树，若存在则进入左子树查询，一直找到无左子树的节点，并放回此时（无左子树）的节点。
public TItem TreeQueryMin(Tree<TItem> tree)
{
    if (tree != null )
    {
        while (tree != null && tree.Left != null )
        {
            tree = tree.Left;
        }
        return tree.NodeDate;
    }
    return default (TItem);
}

二叉树节点的删除：
原理：二叉树节点的删除分为三种情况
    第一种情况为：删除的节点没有左子树（删除下图的值为3的节点）。
    用3与根节点8做比较，3<8，此时则进入当前节点的左子树。此时3==3，那么将此节点删除。

将节点3删除时，用节点8的左孩子，指向被删除节点的左孩子。
即把当前节点（被删除的节点）的左子树，替换为当前节点。这样就不会破坏排序二叉树的平衡性。


第二种情况：删除的节点没有右子树（删除下图的值为10的节点）
原理：用10与根节点8做比较，因为10>8，进入右子树，此时10==10，那么将此节点删除。

将节点10删除时，用节点8的右子树指向被删除节点的右子树。


第三种情况：被删除的节点既包含了左子树，右包含了右子树。也是最复杂的情况，（删除下图值为3的节点）
原理：要删除节点3，从节点3的右子树（被选中的右子树中），找出最小节点，并用找出的最小节点，替换当前被删除的节点，节点3被替换后再删除替换节点4。

删除后，该排序二叉树依然保持平衡性。

第四种情况：是不是以为第三种情况那么复杂，第四种情况要上天了？经过复杂的脑回路思考，咱们休息一下。
    第四种情况为当前节点为叶子节点，那么直接删除就好了~~~是不是so easy？~

C#代码实现：
先定义一个查找右子树最小值的函数。（与二叉树查找最小数的方法略有区别，此函数返回的是最小节点的对象，查找二叉树最小值的方法放回的是一个数值）
public Tree<TItem> FindMinNode(Tree<TItem> tree, TItem item)
{
    if (tree != null )
    {
        while (tree != null && tree.Left != null )
        {
            tree = tree.Left;
        }
    }
    return tree;
}

public Tree<TItem> DeleteTreeNode(Tree<TItem> tree, TItem item)
{
    //如果当前节点为Null,则代表不包含此节点，删除失败
    if (tree == null )
    {
        return null ;
    }
    //如果当前值小于当前节点
    if ( tree.NodeDate.CompareTo(item ) > 0)
    {
        //进入左子树删除
        return DeleteTreeNode(tree.Left, item);
    }
    //如果值大于当前节点
    else if ( tree.NodeDate.CompareTo(item ) < 0)
    {
        //进入右子树删除
        return DeleteTreeNode(tree.Right, item);
    }
    //如果值匹配，则用右子树中的最小值替换该节点
    else
    {
        //判断该节点是否为叶子节点，若为叶子节点，则直接删除
        if (tree.Left == null && tree.Right == null )
        {
            tree = null ;
            return tree;
        }
        //如果当前节点只有右子树
        else if (tree.Left == null )
        {
            //则将当前节点的右子树换成当前节点
            tree = tree.Right;
            //返回被更新过的节点
            return tree;
        }
        //如果当前节点只有左子树
        else if (tree.Right == null )
        {
            //则将当前节点的左子树换成当前节点
            tree = tree.Right;
            //返回被更新过的节点
            return tree;
        }
        //如果当前节点左右子树均存在
        else if (tree.Right != null && tree.Left != null )
        {
            //找出右子树的最小节点，替换当前节点
            tree.NodeDate = FindMinNode(tree, item).NodeDate;
            //删除右子树的最小节点。
            tree.Left = DeleteTreeNode(tree.Right, tree.NodeDate);
            return tree;
        }
    }
    return null ;
}

上述所有方法，均写在  public class Tree < TItem > where TItem : IComparable<TItem> 中
最后简单说下二叉树的实例化、赋值以及调用。
class Program
{
    static void Main(string[] args)
    {
        Tree<int> t = new Tree<int>(8);//定义初始节点
        int[] a = { 3, 10, 1, 6, 4, 7, 14, 13 };
        //插入节点
        foreach (int item in a)
        {
            t.Insert(item);
        }
        Console.WriteLine("二叉树的打印");
        t.TraverseTreePerOrder();
        t.DeleteTreeNode(t, 3);
        Console.WriteLine("删除后，二叉树的打印");
        t.TraverseTreePerOrder();
        Console.Read();
    }
}















利用二叉树的排序算法c#实现
fengzheng22的专栏
12-07 1880
using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace 利用二叉树的排序算法 {     public class Tree     {         public int data;//数据         public Tree lef
堆排序——C#实现
zhuowp的博客
10-16 3554
一 算法描述        堆排序（Heap Sort）是利用一种被称作二叉堆的数据结构进行排序的排序算法。        二叉堆在内部维护一个数组，可被看成一棵近似的完全二叉树，树上每个节点对应数组中的一个元素。除最底层外，该树是满的。        二叉堆中，有两个与所维护数组相关的属性。Length表示数组的元素个数，而HeapSize则表示二叉堆中所维护的数组中的元素的个数（并不是数
c#实现对泛型数组排序
12-26
c#实现对泛型数组排序
二叉树泛型 C#实现
yysdyyyy的博客
03-21 427
C#实现二叉树
排序二叉树C#实现
zhuweisky
07-02 2693
        很久以前写的，现在贴出来交流一下。先看排序二叉树的接口public interface ISorttedBinaryTree {  void InsertElement(IComparable val) ;//如果树中有一个节点的值等于val的值，则val将被忽略  void RemoveElement(IComparable val) ;  bool ContainsElemen
C# 二叉排序树
陈言必行 -- Unity游戏开发领域优质博主
12-24 722
二叉排序树，又称为二叉查找树。它或者是一颗空树，或者是具有下列性质的二叉树：
实现泛型树的多种遍历C#源代码.zip
11-20
通过这些代码，你可以学习如何在C#中使用泛型来创建可扩展的数据结构，并实现不同的遍历算法。这不仅有助于理解和掌握数据结构与算法，还能在实际项目中提升代码的灵活性和可维护性。 总的来说，这个压缩包提供了一...
C#实现二叉树算法详解与代码实践
例如，可以使用C#的泛型来定义类型安全的二叉树，提高代码的复用性。 本资源的文件名“C#_使用C#实现的二叉树算法_算法实现”清楚地表明了资源的性质和内容。读者应该已经具备一定的C#编程基础和数据结构知识，才能...
【记录】C#泛型集合
weixin_46057924的博客
08-20 318
面试时不知觉的提到了泛型集合，索性记录一下 1.从数组说起数组是具有同一类型的多个对象的集合，是一种数据结构，包含同一类型的多个元素。数组是具有同一类型的多个对象的集合，是一种数据结构，包含同一类型的多个元素。 的11111.1211型泛型集合集合概念 ...
C#实现二叉树的添加与删除操作
二叉树的特点和操作是数据结构与算法课程中不可或缺的一部分，尤其在实现搜索、排序和其他复杂数据操作时。 在C#中实现二叉树，首先需要定义树节点的数据结构。一个典型的二叉树节点可能包含数据域和两个指向其左右...
C#简单实现泛型选择排序
04-30
里面包含了泛型选择排序的几个例子，详尽清晰
二叉排序树的C#实现
weixin_30885111的博客
03-26 217
寒假回家的时候，看了一下C#语言描述版的数据结构。我只是单纯的想，更加熟悉计算机语言，我希望能像是用母语一样使用计算机语言和计算机交流。很奇怪之前学C语言版本的数据结构，那些算法我都不是非常理解，但在读这本书的时候，却有种豁然开朗的感觉。是书写的好还是我能力有所提高亦或是两者皆有？ 进入正题。 二叉排序树说起来其实并不是很难。二叉查找树是一种把值比较小的节点存储在左子节点内而值比较大的节点存储...
二叉排序树BST
c梦的博客
02-04 183
What 二叉排序树BST： (Binary Sort Tree 或 Binary Search Tree), 对于二叉排序树的任何一个非叶子节点，要求左子节点的值比当前节点的值小，右子节点的值比当前节点的值大。对于相同的值，可以放在左节点或右节点。 Why 对于数组： 如果数组有序，那么查找速度会很快O(lgn)（使用二分查找），但是增删会很慢（会整体移动数组的一部分会...
二叉排序树的实现（C#）
waterathena的专栏
10-09 1301
  搞了一天终于把这个homework搞定了。开心    ，下个星期有新的任务了。如果所有工作在星期五都可以告于一个段落，对所有职场人来说应该是一件很舒心的事吧。周末可以专注自己的其他事情，不用背着包袱过日子。Wish happy weekend!曾经在网上搜到很多关于一些数据结构的代码，对过往的我的学业带来很大帮助，对现在工作中的我也很有启发。所以现在也把代码共享出来。希望也可以he
C# 泛型List 排序
廷益_飞鸟的博客
05-19 527
代码 using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace Lesson16_List_sort { public class Person:IComparable<Person> { // 属性 public string name; .
C#中集合泛型排序
最新发布
qq_45492643的博客
08-03 252
如果需要自定义排序规则，可以实现接口，并在排序时传入该接口的实现。string// 逆序排序。
C# 泛型集合中的排序
q__y__L的博客
02-13 1347
就算不熟悉Linq，熟悉SQL查询语句的，也能很快上手Linq。List类的Sort方法有4个重载，其中一个是Sort(IComparer comparer)，也就是你可以直接传入一个实现ICompare的对象，Sort方法会调用次对象的固定方法，这里我们将这个特殊的对象叫做。从前面的讨论可以看出最简单的排序方法是利用Linq或者Lambda，另外两种会增加额外的代码量，但是我们应该了解其背后的原理，Linq和Lambda都是C#后面陆续推出的，自然会更能节省开发者时间。
C#泛型快速排序算法
dayssir(时光)的专栏
01-08 1831
快速排序算法是我经常使用的算法，所以也写成了泛型了，省事，不用为每个类型去写个特定的算法了。排序的对象是实现了IList接口的集合。我已经发了一个查找类，经常都要一起使用的。using System;using System.Collections.Generic;using System.Text;using System.Data;namespace CommonLibrary
c#泛型集合排序
weixin_34001430的博客
05-13 249
c#泛型集合排序总结 今天学习学累了，还有一点时间就总结一下重要的知识点吧！也算复习了！ 排序有很多方法其中有很多都是被接受的（即老师上课讲的），当时虽然也会用但是很不理解为什么要这样做，这样做为什么能实现，其实细研究一下也没什么，只不过微软给我们封装了很多东西，所以导致现在学习编程的人，尤其是学习所谓的高级语言的人，都只知道什么东西怎么用，能干什么，更多的是去关心业务逻...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值