数据结构——树状数组

最新推荐文章于 2023-01-04 17:06:39 发布

Wayward：)

最新推荐文章于 2023-01-04 17:06:39 发布

阅读量406

点赞数 1

分类专栏： ==== 数据结构与算法 ==== 文章标签：高级数据结构树状数组

原文链接：https://bestsort.cn/2019/04/26/195/

版权

==== 数据结构与算法 ==== 专栏收录该内容

19 篇文章 11 订阅

订阅专栏

文章目录

1.树状数组的基础

树状数组 是一个查询和修改复杂度都在 $O (l o g n)$ 的数据结构，主要用于数组的单点修改和区间求和。

一般，我们常见的二叉树是这样画的：
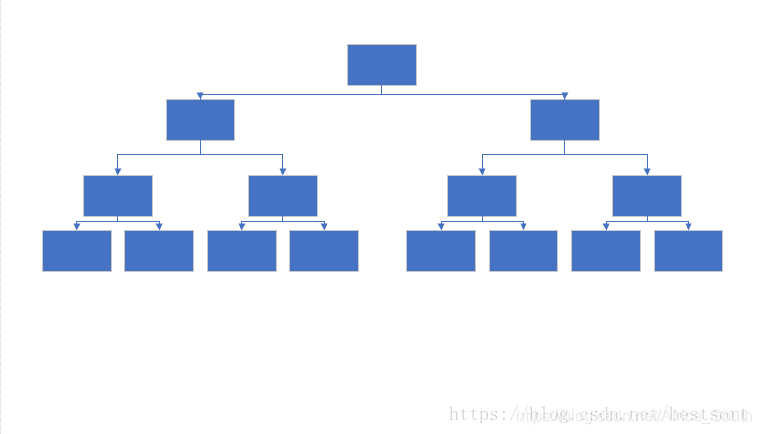
普通二叉树
叶子节点代表A数组，A[1]~A[8]。

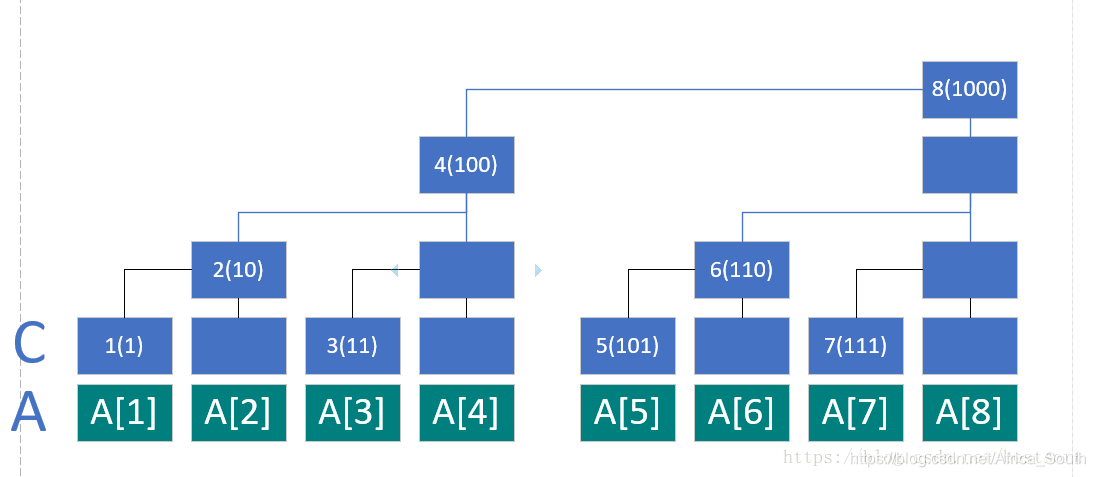
然后，我们稍微变行一下，就形成了树状数组的画法：

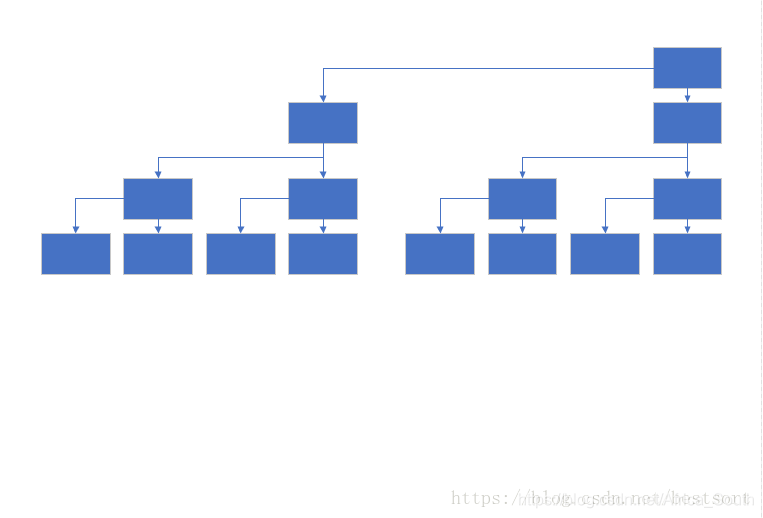
从上图，我们可以看出来，最后的根结点其实可以看成所有叶子结点求和的结果，而内部结点可以看成是叶子结点分段求和的结果，如下图所示：
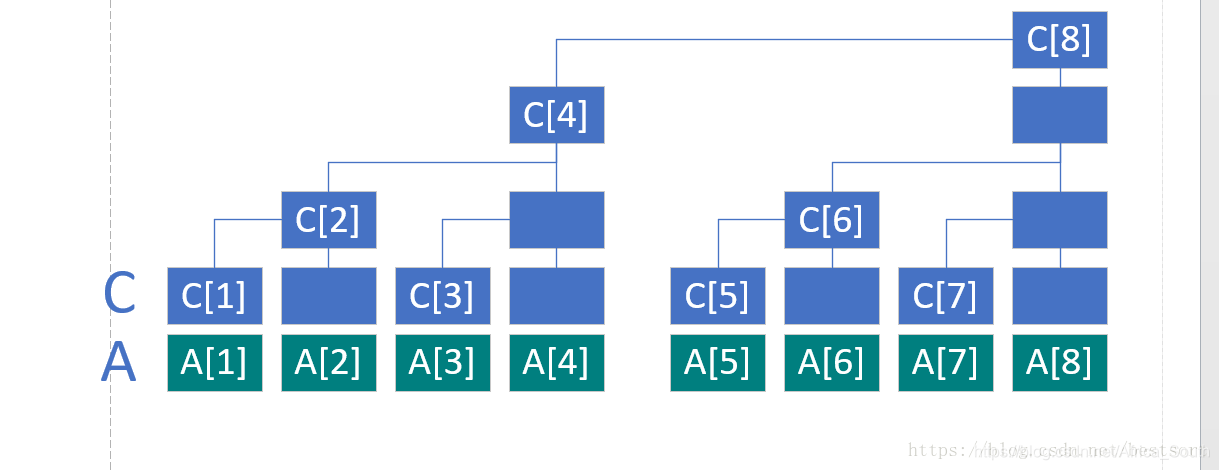
区间求和示意图
从上图我们可以看出来，A数组是原始数组，代表叶子结点，C数组是求和后的数组，代表内部结点。
且 $C [i]$ 代表子树叶子结点的权值之和，即

C[1] = A[1]
C[2] = A[1] + A[2]
C[3] = A[3]
C[4] = A[1] + A[2] + A[3] + A[4]
C[5] = A[5]
C[6] = A[5] + A[6]
C[7] = A[7]
C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]

再将其转成二进制形式有

C[1] = C[0001] = C[1-0,1] = A[1];                   
C[2] = C[0010] = C[2-1,1] = A[1] + A[2]
C[3] = C[0011] = c[3-0,3] = A[3]
C[4] = C[0100] = C[4-3,4] = A[1] + A[2] + A[3] + A[4]
C[5] = C[0101] = C[5-0,5] = A[5]
C[6] = C[0110] = C[6-1,6] = A[5] + A[6]
C[7] = C[0111] = C[7-0,7] = A[7]
C[8] = C[1000] = C[8-7,8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]

对照式子可以发现 $C[i] = A[i-(2^k-1)]+...+A[i]$
其中 $k$ 为 $i$ 的二进制中从低位开始到高位连续的0，例如 $i = 8 (1000)$ 时, $k = 3$ ，则
$C[8] = A[8 - 2^3+1]+A[8-2^3+2]+...+A[8]$ 就是上面列出的树状数组。
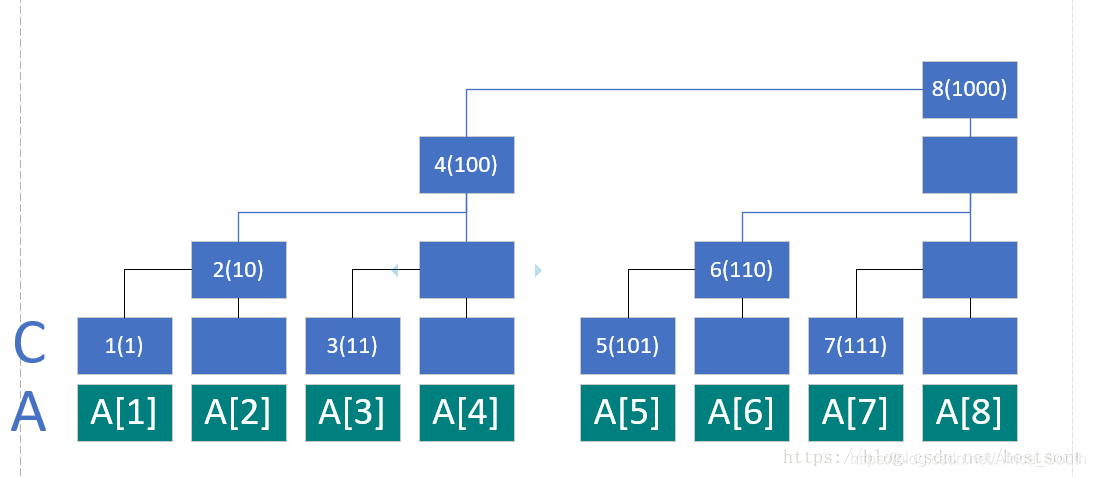
树状数组示例
则我们也有一个明显的结果，二进制低位有k个连续的0，则该结点就是子树 $2^k$ 个叶子结点的和。

下面我们介绍一种简单粗暴的技术来求解低位有几个连续的0。
令 lowbit(x) 表示求x最低位的1以及在其后补0，则容易看出lowbit(i)就是上面 $2^k$ ，因为 $2^k$ 后面有k个0才是第一个1。例如 $2^3=1000$ 正好是 i 的最低位的1加上后缀0所得到的值。则我们有lowbit(i)的计算方法

int lowbit(x){
	return x & (-x);
}

解释一下：
对于一个数（计算机中存储的是二进制数），求其负数就是对其取反+1，也就是取补的过程，例如
6(00110)->取反11001->加1得11010(-6)-> 相与有00010恰好表示有1个连续的0，
即反码和原码的0/1是相反的，则原码低位连续的0取反后全是1，加上1后，全变0，而进位的1恰好是原码第一个1的位置，此时高位是相反的，所以取与恰好能把这个位置的1取出来。

2.树状数组的基本操作

2.1.单点更新

在这里插入图片描述
若此时我们要更改A[1]，则需要进行下面的同步更新：

1(0001)
C[1] += A[1]
lowbit(1)=001 1+lowbit(1)=2(010) C[2]+=A[1]
lowbit(2)=010 2+lowbit(2)=4(100) C[4]+=A[1]
lowbit(4)=100 4+lowbit(4)=8(1000) C[8]+=A[1]

若更新A[3]则有一下同步更新：

3(0011)
C[3] += A[3]
lowbit(3) =001 3+lowbit(3)=4(100) C[4]+=A[3]
lowbit(4)=100 4+lowbit(4)=8(1000) C[8]+=A[3]

此时会发现这是一个递推的过程，则有代码：

void update(int x,int y,int n){
	// x 为更新的位置,y为更新后的数，n为数组的上界
	for(int i=x;i<=n;i+=lowbit(i)) c[i]+=y;
}

我们可以看到这个更新是按照树结构往上传的，所以复杂度在 $O (l o g n)$

2.2 区间查询

举个例子，求sum(5)
则有

C[4] = C[0100] = A[1] + A[2] + A[3] + A[4]
C[5] = C[0101] = A[5]
sum(i == 5) = C[4] + C[5],
即 sum(101) = C[100] + C[101] = C[101-lowbit(101)] + C[101]

也就是单点更新的逆操作，即减lowbit()，复杂度在 $O (l o g n)$ ，代码如下：

int getsum(int x){
	int sum = 0;
	for(int i=x;i;i-=lowbit(i)) sum += c[i];
	return sum;
}

2.3 例题练习

HDU1166 敌兵布阵单点更新+区间查询

/* HDU 1166 敌兵布阵*/
#include <iostream>
#include <string>

#define lowbit(x) ((x)&(-x))

using namespace std;

const int MAXN = 5 * 1e4 + 5;
int c[MAXN];
void update(int x, int y, int n) {
	for (int i = x; i <= n; i += lowbit(i)) c[i] += y;
}
int getsum(int x) {
	int sum = 0;
	for (int i = x; i; i -= lowbit(i)) sum += c[i];
	return sum;
}
int main() {
	int t, n;
	int x, y, z;
	scanf("%d", &t);
	for (int i = 1; i <= t; i++) {
		scanf("%d", &n);
		// 初始化数组中前n+1个数字为0
		fill(c, c + n + 1, 0);
		for (int j = 1; j <= n; j++) {
			scanf("%d", &z);
			update(j, z, n); // 表明开始建树
		}
		printf("Case %d:\n", i);
		while (1) { // 开始查询
			string s;
			cin >> s;
			if (s[0] == 'E') break;
			scanf("%d%d", &x, &y);
			if (s[0] == 'Q') printf("%d\n", getsum(y) - getsum(x - 1));
			else if (s[0] == 'A') update(x, y, n);
			else update(x, -y, n);
		}
	}

	return 0;
}

即初始插入建树状数组操作时使用基本的更新操作update来建立。

以上部分引用自bestsort 的博客

3.高级应用

3.1 求逆序对

数组离散化
对于输入的数组A，由于求逆序数只需要知道元素间的相对大小，所以我们可以使用下列方式对输入进行离散化：

for(int i=1;i<=n;i++){
	a[i].data = read();
	a[i].id = i;
}
sort(a+1,a+n+1); // 按照data升序排列
for(int i=1;i<=n;i++) b[a[i].id] = i;

举个栗子
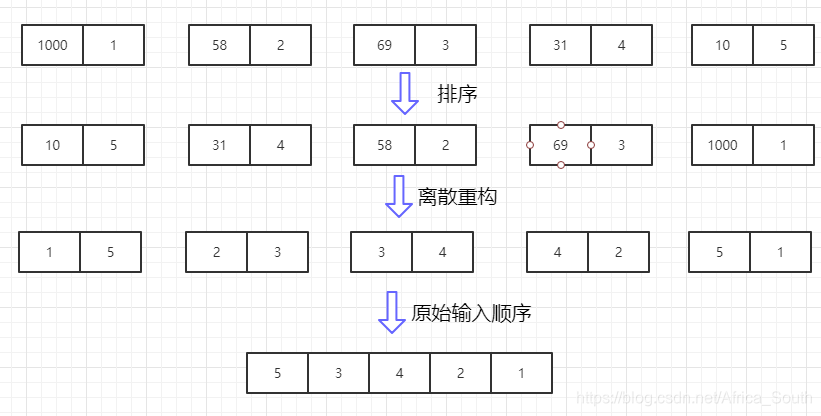
离散化举例
所以最后我们得到原始输入的相对顺序，[5,3,4,2,1] 排名越靠后表明数字越大，这样的预处理也能够避免输入的数据太大，因为我们只需要相对顺序就行。

逆序数

逆序对即在一个序列中，如果存在 $i < j 且 a [i] > a [j]$ ，那么就表明有一个逆序对。即对于每一个位置的数，我么考虑出现在它之前的数有多少比它大，就构成一个逆序，然后我们考虑完所有位置后，就可求出总的逆序数。

我们从 $1 到 n$ 开始枚举，对于位置 $i$ 的数，我们在数组中将其标识为1代表其出现过，然后考虑比它先出现的数（小于它）有多少个，即树状数组中的区间求和操作getsum[i](小于等于的数)，此时我们已经插入i个数，所以比它大的就有i-getsum[i]个，遍历n遍即可求出总的逆序数，复杂度在 $O (n l o g n)$ 。

// -- 使用树状数组求逆序对 -- 
// 复杂度为nlogn, 包含离散化和建树查询
#include<vector>
#include<algorithm>
#include<string>
#include<iostream>

#define lowbit(x) (x)&(-x)

using namespace std;

typedef struct {
	int d, id; // 输入的数据和原始顺序
}node;

vector<node> a; // 原始的数据顺序
vector<int> b;  // 离散化后的数据，小的在前面，存储原始数据在全部数据中排第几
vector<int> c;  // 为最后的求和数组
int n;          // 数组长度
int DEBUG = 1;

int cmp(node p, node q) {
	return p.d < q.d;
}
void update(int x, int y) {
	while (x <= n) {
		c[x] += y;
		x += lowbit(x);
	}
}
int getsum(int x) {
	int sum = 0;
	while (x) {
		sum += c[x];
		x -= lowbit(x);
	}
	return sum;
}

int main() {
	cin >> n;
	a.resize(n + 1); b.resize(n + 1); c.resize(n + 1);
	int i, j, e;
	for (i = 1; i <= n; i++) {
		cin >> e;
		a[i] = { e,i };
	}
	// 排序，从1开始
	sort(a.begin() + 1, a.end(), cmp);
	// 开始离散化,b[]表明该位置的元素在原始位置排第几，越大越排在后面
	for (i = 1; i <= n; i++) b[a[i].id] = i;
	if (DEBUG) {
		printf("排序完成后的相对位置:");
		for (i = 1; i <= n; i++) printf("%d ", b[i]);
		printf("\n");
	}
	// 开始建立树和求逆序对
	fill(&c[0], &c[n], 0);
	int cnt = 0;
	for (i = 1; i <= n; i++) {
		update(b[i], 1); // 表明排名第b[i]的数据出现过了
		cnt += (i - getsum(b[i]));
		// getsum(b[i])表明小于等于b[i]的元素个数
		// i 表明当前插入的元素个数，想减表示大于等于b[i]的元素
		if (DEBUG) printf("第%d位时候的逆序数%d\n", i, cnt);
	}
	system("pause");
	return 0;
}

我们以之前的例子说明，同时直接以离散化后的顺序说明：
上面表示数据数组，下面表示标记数组
在这里插入图片描述
第一次插入，把5的位置标记成1，此时getsum[5]=1，表明小于等于它的只有它自己，大于它的为1 - 1 = 0

第二次插入，把3的位置标记成，这是getsum[3] = 1，表面大于它的有2 - 1 = 1

第三次插入，把4的位置标记成，这是getsum[4] = 2，表面大于它的有3 - 2 = 1
在这里插入图片描述
第四次插入，把2的位置标记成，这是getsum[2] = 1，表面大于它的有4 - 1 = 3

第五次插入，把1的位置标记成，这是getsum[1] = 1，表面大于它的有5 - 1 = 4
所以总的逆序数为9。

图源SSimpLe_Y的博客

3.2 稍进阶操作

1. 区间修改 + 单点查询
通过差分，将此问题转换为基本的单点修改+区间查询。

– 查询
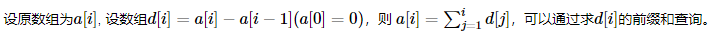
在这里插入图片描述
– 修改

void update(int p,int x){
		for(int i=p;i<=n;i += lowbit(i)) a[i] += x;
}
void range_update(int l,int r,int x){
	update(l,x); // 给[l,]加上x
	update(r + 1,-x); // 给[r+1,]减去x
	// 即给[l,r]加上x
}
void getsum(int p){ // 单点查询
	int sum = 0;
	for(int i=p;i;i -= lowbit(i)) sum += a[i];
	return sum;
}

2.区间修改+区间查询

基于上面1的的“差分”，我们可以在树状数组中求数组的前缀和，即
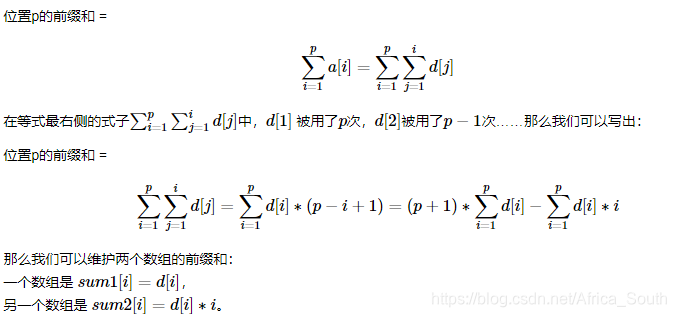
在这里插入图片描述
–查询

位置p的前缀和即： $(p + 1) * s u m 1$ 数组中p的前缀和（区间查询） - $s u m 2$ 数组中p的前缀和
区间 $[l, r]$ 的和即：位置 $r$ 的前缀和-位置 $l - 1$ 的前缀和

–修改

对sum1数组的修改和之前的一样。
对sum2的修改，我们给 $s u m 2 [l] 加上 l * x$ 。

void update(int p,int x){
		for(int i=p;i<=n;i += lowbit(i)){
			sum1[i] += x, sum2[i] += p * x;
		}
}
void update(int l,int r,int x){
	update(l,x); update(r+1,-x);
}
void getsum(int p){ // 单点查询
	int sum = 0;
	for(int i=p;i;i -= lowbit(i)) sum += (p+1)*sum1[i] - sum2[i];
	return sum;
}

以上部分内容来自胡小兔的Blog

4.例题收录

Wayward：)

关注

1
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
数据结构——树状数组

文章目录1.树状数组的基础2.树状数组的基本操作2.1.单点更新2.2 区间查询2.3 例题练习3.高级应用3.1 求逆序对3.2 稍进阶操作4.例题收录1.树状数组的基础树状数组是一个查询和修改复杂度都在O(logn)O(logn)O(logn) 的数据结构，主要用于数组的单点修改和区间求和。一般，我们常见的二叉树是这样画的：叶子节点代表A数组，A[1]~A[8]。然后，我们稍微变...
复制链接

扫一扫