给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
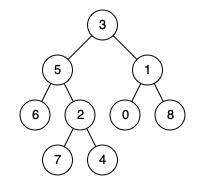
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点5和节点1的最近公共祖先是节点3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点5和节点4的最近公共祖先是节点5。因为根据定义最近公共祖先节点可以为节点本身。
算法逻辑
Hello_World我又回来了,当然不用在意这句,我们直接开干
其实此题真正考察的内容是对递归的掌握,递归递归,也就是递推 && 回归
left = public_ancestors(root.left, num_0, num_1)
递归地在左子树中查找num_0和num_1的最近公共祖先,将结果存储在变量left中。
right = public_ancestors(root.right, num_0, num_1)
递归地在右子树中查找num_0和num_1的最近公共祖先,将结果存储在变量right中
def public_ancestors(root, num_0, num_1):
if root is None or root.data == num_0 or root.data == num_1:
return root
else:
left = public_ancestors(root.left, num_0, num_1)
right = public_ancestors(root.right, num_0, num_1)
if left and right:
return root
return left if left else right(寻找最近公共祖先代码)
当left和right都不为空时:说明当前节点root为num_0与num_1的最近公共祖先,返回root
当left不为空而right为空:说明num_0和num_1都在左子树中,因此返回left
当right不为空而left为空:说明num_0和num_1都在右子树中,因此返回right
完整代码
class node:
def __init__(self,data):
self.data = data
self.right = None
self.left = None
def public_ancestors(root, num_0, num_1):
if root is None or root.data == num_0 or root.data == num_1:
return root
else:
left = public_ancestors(root.left, num_0, num_1)
right = public_ancestors(root.right, num_0, num_1)
if left and right:
return root
return left if left else right
tree = node(3)
tree.left = node(1)
tree.right = node(4)
tree.right.left = node(2)
tree.right.right = node(5)
print(public_ancestors(tree, 1, 5).data)
希望此篇文章对你有帮助,也请您不要忘记点击关注支持一下博主,不过最重要的是:
自己试试看吧,你可以做的更好!
























 307
307

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








