JZOJ4727. 挺进

题目大意

给定一棵$n$个点的树，每条边有边权。现在选择一条边将它删除，得到两个联通块，要求最大的联通块直径之和是多少。

Data Constraint
$n\leq100000$

题解

先给出一个结论：两个联通块合并后的新直径必然是由两条旧直径的端点组合而成。
也就是说，我们可以比较容易地合并两个联通块。然后考虑用线段树维护DFS序上的联通块直径，线段树上一个区间即代表DFS序对应区间的结点构成的联通块。
然后枚举删除哪条边，再在线段树上查询对应的区间即可。

然而这样是$log^2$因为合并直径的时候用倍增求LCA还要一个$log$，所以会T。
用RMQ求LCA问题就解决了。

---

RMQ求LCA

用RMQ可以实现$O(n)$求树上两点的LCA。
记录一个$S$数组，每次DFS到某个点的时候就加入$S$数组，“到”并不是指DFS那种第一次“到”，是每次都加入。可以证明最终$S$数组内会有$2n+1$个数。
再记一个数组$P$，$P_i$表示$S_i$在树中的深度是$P_i$。
举个栗子：

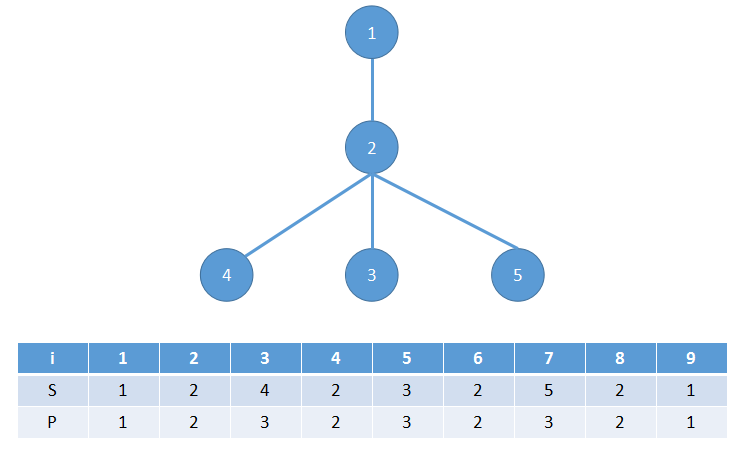
然后记$First_i$表示$i$结点在$S$中第一次出现的位置。
对于一个询问$(x,y)$，它们的LCA就是$[First_x,First_y]$中深度最小的结点。
正确性：$[First_x,First_y]$中深度小于$x,y$的点都在$x \to y$的路径上，而深度最小的那个点就必然是LCA了。

SRC

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std ;

#define N 100000 + 10
typedef long long ll ;
const int MAXN = 19 ;
struct Note {
    int a , b ;
    ll len ;
    Note ( int X = 0 , int Y = 0 , ll Z = 0 ) { a = X , b = Y , len = Z ; }
} T[4*N] , ret ;

int tab[2*N] ;
int RMQ[2*N][MAXN] ;
int Node[2*N] , Next[2*N] , Len[2*N] , Head[N] , tot = 1 ;
int S[2*N] , P[2*N] , Fir[N] , Dep[N] ;
int E[N] , D[N] , R[N] , DFN[N] ;
ll ans , Dist[N] ;
int n ;

void link( int u , int v , int w ) {
    Node[++tot] = v ;
    Next[tot] = Head[u] ;
    Len[tot] = w ;
    Head[u] = tot ;
}

void DFS( int x , int Fa ) {
    D[++D[0]] = x ;
    S[++S[0]] = x ;
    P[S[0]] = Dep[x] ;
    Fir[x] = S[0] , DFN[x] = D[0] ;
    for (int p = Head[x] ; p ; p = Next[p] ) {
        if ( Node[p] == Fa ) continue ;
        Dep[Node[p]] = Dep[x] + 1 ;
        Dist[Node[p]] = Dist[x] + Len[p] ;
        DFS( Node[p] , x ) ;
        S[++S[0]] = x ;
        P[S[0]] = Dep[x] ;
        R[x] = D[0] ;
    }
}

void Pre() {
    for (int i = 1 ; i <= S[0] ; i ++ ) RMQ[i][0] = i , tab[i] = log(i) / log(2) ;
    for (int j = 1 ; j < MAXN ; j ++ ) {
        for (int i = 1 ; i <= S[0] ; i ++ )  {
            RMQ[i][j] = RMQ[i][j-1] ;
            if ( i + (1 << (j-1)) <= S[0] && P[RMQ[i+(1<<(j-1))][j-1]] < P[RMQ[i][j]] ) RMQ[i][j] = RMQ[i+(1<<(j-1))][j-1] ;
        }
    }
}

int Find( int l , int r ) {
    int k = tab[r-l+1] ;
    if ( P[RMQ[l][k]] < P[RMQ[r-(1<<k)+1][k]] ) return RMQ[l][k] ;
    return RMQ[r-(1<<k)+1][k] ;
}

int LCA( int x , int y ) {
    if ( Fir[x] > Fir[y] ) swap( x , y ) ;
    return S[Find(Fir[x],Fir[y])] ;
}

ll Calc( int x , int y ) {
    return Dist[x] + Dist[y] - 2 * Dist[LCA(x,y)] ;
}

Note Merge( Note x , Note y ) {
    Note ret = (x.len > y.len ? x : y) ;
    if ( Calc(x.a,y.a) > ret.len ) ret = Note( x.a , y.a , Calc(x.a,y.a) ) ;
    if ( Calc(x.a,y.b) > ret.len ) ret = Note( x.a , y.b , Calc(x.a,y.b) ) ;
    if ( Calc(x.b,y.a) > ret.len ) ret = Note( x.b , y.a , Calc(x.b,y.a) ) ;
    if ( Calc(x.b,y.b) > ret.len ) ret = Note( x.b , y.b , Calc(x.b,y.b) ) ;
    return ret ;
}

void Build( int v , int l , int r ) {
    if ( l == r ) {
        T[v].a = T[v].b = D[l] ;
        return ;
    }
    int mid = (l + r) / 2 ;
    Build( v + v , l , mid ) ;
    Build( v + v + 1 , mid + 1 , r ) ;
    T[v] = Merge( T[v+v] , T[v+v+1] ) ;
}

void Search( int v , int l , int r , int x , int y ) {
    if ( x > y ) return ;
    if ( l == x && r == y ) {
        ret = Merge( ret , T[v] ) ;
        return ;
    }
    int mid = (l + r) / 2 ;
    if ( y <= mid ) Search( v + v , l , mid , x , y ) ;
    else if ( x > mid ) Search( v + v + 1 , mid + 1 , r , x , y ) ;
    else {
        Search( v + v , l , mid , x , mid ) ;
        Search( v + v + 1 , mid + 1 , r , mid + 1 , y ) ;
    }
}

int main() {
    scanf( "%d" , &n ) ;
    for (int i = 1 ; i < n ; i ++ ) {
        int u , v , w ;
        scanf( "%d%d%d" , &u , &v , &w ) ;
        link( u , v , w ) ;
        link( v , u , w ) ;
        E[++E[0]] = tot ;
    }
    Dist[1] = 0 ;
    Dep[1] = 1 ;
    DFS( 1 , 0 ) ;
    Pre() ;
    Build( 1 , 1 , n ) ;
    for (int i = 1 ; i <= E[0] ; i ++ ) {
        int x = Node[E[i]] ;
        int y = Node[E[i]^1] ;
        if ( Dep[x] > Dep[y] ) swap( x , y ) ;
        ret.a = ret.b = y ;
        ret.len = 0 ;
        Search( 1 , 1 , n , DFN[y] , R[y] ) ;
        ll tp = ret.len ;
        ret.a = ret.b = x ;
        ret.len = 0 ;
        Search( 1 , 1 , n , 1 , DFN[y] - 1 ) ;
        Search( 1 , 1 , n , R[y] + 1 , n ) ;
        tp += ret.len ;
        ans = max( ans , tp ) ;
    }
    printf( "%lld\n" , ans ) ;
    return 0 ;
}

以上.