第一个编程任务
任务目标:
-
学会使用 iPython Notebooks
-
学会使用numpy函数并使用numpy进行矩阵和向量操作
-
理解“广播”这一概念
-
能够使用向量化进行代码实现
"""
Python Basics with Numpy (optional assignment)
Welcome to your first assignment. This exercise gives you a brief introduction to Python. Even if you've used Python before, this will help familiarize you with functions we'll need.
Instructions:
You will be using Python 3.
Avoid using for-loops and while-loops, unless you are explicitly told to do so.
Do not modify the (# GRADED FUNCTION [function name]) comment in some cells. Your work would not be graded if you change this. Each cell containing that comment should only contain one function.
After coding your function, run the cell right below it to check if your result is correct.
After this assignment you will:
Be able to use iPython Notebooks
Be able to use numpy functions and numpy matrix/vector operations
Understand the concept of "broadcasting"
Be able to vectorize code
Let's get started!
"""关于 iPython Notebooks的介绍
"""
iPython Notebooks are interactive coding environments embedded in a webpage.
You will be using iPython notebooks in this class.
You only need to write code between the
### START CODE HERE ### and
### END CODE HERE ### comments.
After writing your code, you can run the cell by either pressing "SHIFT"+"ENTER" or by clicking on "Run Cell" (denoted by a play symbol) in the upper bar of the notebook.
We will often specify "(≈ X lines of code)" in the comments to tell you about how much code you need to write. It is just a rough estimate, so don't feel bad if your code is longer or shorter.
"""
练习1:打印Hello World
"""
Exercise: Set test to "Hello World" in the cell below to print "Hello World" and run the two cells below.
"""
### START CODE HERE ### (≈ 1 line of code)
test = "Hello World"
### END CODE HERE ###
print ("test: " + test)
#Expected output: test: Hello World构建关于numpy的基本函数
"""
1 - Building basic functions with numpy
Numpy is the main package for scientific computing in Python. It is maintained by a large community (www.numpy.org). In this exercise you will learn several key numpy functions such as np.exp, np.log, and np.reshape. You will need to know how to use these functions for future assignments.
""使用np.exp()来进行sigmoid函数的实现
"""
1.1 - sigmoid function, np.exp()
Before using np.exp(), you will use math.exp() to implement the sigmoid function. You will then see why np.exp() is preferable to math.exp().
""练习2:使用math.exp()构建输入x,返回sigmoid(x)的函数
| 提示: |
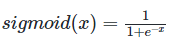
|
"""
Exercise: Build a function that returns the sigmoid of a real number x. Use math.exp(x) for the exponential function.
Reminder:sigmoid(x) is sometimes also known as the logistic function. It is a non-linear function used not only in Machine Learning (Logistic Regression), but also in Deep Learning.
To refer to a function belonging to a specific package you could call it using package_name.function(). Run the code below to see an example with math.exp().
"""
# GRADED FUNCTION: basic_sigmoid
import math
"""
def basic_sigmoid(x):
return 1/(1+math.exp(-x))
"""
def basic_sigmoid(x):
"""
Compute sigmoid of x.
Arguments:
x -- A scalar
Return:
s -- sigmoid(x)
"""
### START CODE HERE ### (≈ 1 line of code)
s = 1/(1+math.exp(-x))
### END CODE HERE ###
return s
basic_sigmoid(3)
#Expected output: basic_sigmoid(3) ** 0.9525741268224334在深度学习中,我们实际上很少使用math这一函数库,因为这一函数库的输入大多数情况下是一个实数,二在深度学习中,我们经常使用的数据输入是矩阵或者向量,所以在深度学习领域numpy这一函数库更加实用
Actually, we rarely use the "math" library in deep learning because the inputs of the functions are real numbers. In deep learning we mostly use matrices and vectors. This is why numpy is more useful.
### One reason why we use "numpy" instead of "math" in Deep Learning ###
x = [1, 2, 3]
basic_sigmoid(x) # you will see this give an error when you run it, because x is a vector.
In fact, if $ x = (x_1, x_2, ..., x_n)$ is a row vector then $np.exp(x)$ will apply the exponential function to every element of x. The output will thus be: $np.exp(x) = (e^{x_1}, e^{x_2}, ..., e^{x_n})$
import numpy as np
# example of np.exp
x = np.array([1, 2, 3])
print(np.exp(x)) # result is (exp(1), exp(2), exp(3))
Furthermore, if x is a vector, then a Python operation such as $s = x + 3$ or $s = \frac{1}{x}$ will output s as a vector of the same size as x.
# example of vector operation
x = np.array([1, 2, 3])
print (x + 3)
Any time you need more info on a numpy function, we encourage you to look at [the official documentation](https://docs.scipy.org/doc/numpy-1.10.1/reference/generated/numpy.exp.html).
You can also create a new cell in the notebook and write `np.exp?` (for example) to get quick access to the documentation.
练习3:使用numpy实现sigmoid函数
Any time you need more info on a numpy function, we encourage you to look at [the official documentation](https://docs.scipy.org/doc/numpy-1.10.1/reference/generated/numpy.exp.html).
You can also create a new cell in the notebook and write `np.exp?` (for example) to get quick access to the documentation.
**Exercise**: Implement the sigmoid function using numpy.
**Instructions**: x could now be either a real number, a vector, or a matrix. The data structures we use in numpy to represent these shapes (vectors, matrices...) are called numpy arrays. You don't need to know more for now.
$$ \text{For } x \in \mathbb{R}^n \text{, } sigmoid(x) = sigmoid\begin{pmatrix}
x_1 \\
x_2 \\
... \\
x_n \\
\end{pmatrix} = \begin{pmatrix}
\frac{1}{1+e^{-x_1}} \\
\frac{1}{1+e^{-x_2}} \\
... \\
\frac{1}{1+e^{-x_n}} \\
\end{pmatrix}\tag{1} $$
# GRADED FUNCTION: sigmoid
import numpy as np # this means you can access numpy functions by writing np.function() instead of numpy.function()
"""
def sigmoid(x):
return 1/(1+np.exp(-x))
"""
def sigmoid(x):
"""
Compute the sigmoid of x
Arguments:
x -- A scalar or numpy array of any size
Return:
s -- sigmoid(x)
"""
### START CODE HERE ### (≈ 1 line of code)
s = 1/(1+np.exp(-x))
### END CODE HERE ###
return s
x = np.array([1,2,3])
sigmoid(x)
#Expected Output: **sigmoid([1,2,3])** array([ 0.73105858, 0.88079708, 0.95257413])1.2 - Sigmoid gradient
As you've seen in lecture, you will need to compute gradients to optimize loss functions using backpropagation. Let's code your first gradient function.练习4:使用sigmoid_grad()来计算sigmoid函数的梯度,其中sigmoid的输入是x
**Exercise**: Implement the function sigmoid_grad() to compute the gradient of the sigmoid function with respect to its input x. The formula is: $$sigmoid\_derivative(x) = \sigma'(x) = \sigma(x) (1 - \sigma(x))\tag{2}$$
You often code this function in two steps:
1. Set s to be the sigmoid of x. You might find your sigmoid(x) function useful.
2. Compute $\sigma'(x) = s(1-s)$
# GRADED FUNCTION: sigmoid_derivative
"""
def sigmoid_derivative(x):
return ((1/(1 + np.exp(-x))) * (1 - 1 / (1 + np.exp(-x))))
"""
def sigmoid_derivative(x):
"""
Compute the gradient (also called the slope or derivative) of the sigmoid function with respect to its input x.
You can store the output of the sigmoid function into variables and then use it to calculate the gradient.
Arguments:
x -- A scalar or numpy array
Return:
ds -- Your computed gradient.
"""
### START CODE HERE ### (≈ 2 lines of code)
ds = ((1/(1 + np.exp(-x))) * (1 - 1 / (1 + np.exp(-x))))
### END CODE HERE ###
return ds
x = np.array([1, 2, 3])
print ("sigmoid_derivative(x) = " + str(sigmoid_derivative(x)))
#Expected Output:**sigmoid_derivative([1,2,3])** [ 0.19661193 0.10499359 0.04517666对输入矩阵进行维数变换,注意变换前后的矩阵元素数量要保持一致
### 1.3 - Reshaping arrays ###
Two common numpy functions used in deep learning are [np.shape](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.shape.html) and [np.reshape()](https://docs.scipy.org/doc/numpy/reference/generated/numpy.reshape.html).
- X.shape is used to get the shape (dimension) of a matrix/vector X.
- X.reshape(...) is used to reshape X into some other dimension.
For example, in computer science, an image is represented by a 3D array of shape $(length, height, depth = 3)$. However, when you read an image as the input of an algorithm you convert it to a vector of shape $(length*height*3, 1)$. In other words, you "unroll", or reshape, the 3D array into a 1D vector.
<img src="images/image2vector_kiank.png" style="width:500px;height:300;">
**Exercise**: Implement `image2vector()` that takes an input of shape (length, height, 3) and returns a vector of shape (length\*height\*3, 1). For example, if you would like to reshape an array v of shape (a, b, c) into a vector of shape (a*b,c) you would do:
``` python
v = v.reshape((v.shape[0]*v.shape[1], v.shape[2])) # v.shape[0] = a ; v.shape[1] = b ; v.shape[2] = c
```
- Please don't hardcode the dimensions of image as a constant. Instead look up the quantities you need with `image.shape[0]`, etc.
# GRADED FUNCTION: image2vector
"""
def image2vector(image):
return image.reshape(image.shape[0]*image.shape[1]*image.shape[2],1)
"""
def image2vector(image):
"""
Argument:
image -- a numpy array of shape (length, height, depth)
Returns:
v -- a vector of shape (length*height*depth, 1)
"""
### START CODE HERE ### (≈ 1 line of code)
v = mage.reshape(image.shape[0]*image.shape[1]*image.shape[2],1)
### END CODE HERE ###
return v
image = np.array([[[ 0.67826139, 0.29380381],
[ 0.90714982, 0.52835647],
[ 0.4215251 , 0.45017551]],
[[ 0.92814219, 0.96677647],
[ 0.85304703, 0.52351845],
[ 0.19981397, 0.27417313]],
[[ 0.60659855, 0.00533165],
[ 0.10820313, 0.49978937],
[ 0.34144279, 0.94630077]]])
print("image2vector(image) = " + str(image2vector(image)))
"""
#Expected Output:
image2vector(image) = [[0.67826139]
[0.29380381]
[0.90714982]
[0.52835647]
[0.4215251 ]
[0.45017551]
[0.92814219]
[0.96677647]
[0.85304703]
[0.52351845]
[0.19981397]
[0.27417313]
[0.60659855]
[0.00533165]
[0.10820313]
[0.49978937]
[0.34144279]
[0.94630077]]
"""
规范化向量,使得向量的值介于0~1之间,这样会使得梯度下降收敛更快,并且能够使模型的变现更好
### 1.4 - Normalizing rows
Another common technique we use in Machine Learning and Deep Learning is to normalize our data. It often leads to a better performance because gradient descent converges faster after normalization. Here, by normalization we mean changing x to $ \frac{x}{\| x\|} $ (dividing each row vector of x by its norm).
For example, if $$x =
\begin{bmatrix}
0 & 3 & 4 \\
2 & 6 & 4 \\
\end{bmatrix}\tag{3}$$ then $$\| x\| = np.linalg.norm(x, axis = 1, keepdims = True) = \begin{bmatrix}
5 \\
\sqrt{56} \\
\end{bmatrix}\tag{4} $$and $$ x\_normalized = \frac{x}{\| x\|} = \begin{bmatrix}
0 & \frac{3}{5} & \frac{4}{5} \\
\frac{2}{\sqrt{56}} & \frac{6}{\sqrt{56}} & \frac{4}{\sqrt{56}} \\
\end{bmatrix}\tag{5}$$ Note that you can divide matrices of different sizes and it works fine: this is called broadcasting and you're going to learn about it in part 5.
**Exercise**: Implement normalizeRows() to normalize the rows of a matrix. After applying this function to an input matrix x, each row of x should be a vector of unit length (meaning length 1).
# GRADED FUNCTION: normalizeRows
"""
def normalizeRows(x):
return x / np.linalg.norm( x,ord = 2 , axis=1 ,keepdims=True)
"""
def normalizeRows(x):
"""
Implement a function that normalizes each row of the matrix x (to have unit length).
Argument:
x -- A numpy matrix of shape (n, m)
Returns:
x -- The normalized (by row) numpy matrix. You are allowed to modify x.
"""
### START CODE HERE ### (≈ 2 lines of code)
# Compute x_norm as the norm 2 of x. Use np.linalg.norm(..., ord = 2, axis = ..., keepdims = True)
norm = np.linalg.norm(x,ord = 2 , axis=1 ,keepdims=True)
# Divide x by its norm.
x = x / norm
### END CODE HERE ###
return x
x = np.array([
[0, 3, 4],
[1, 6, 4]])
print("normalizeRows(x) = " + str(normalizeRows(x)))
"""
Expected Output:normalizeRows(x) = [[0. 0.6 0.8 ]
[0.13736056 0.82416338 0.54944226]]
"""在规范化向量函数中,你可以尝试打印x_norm和x的维度,你会发现它们俩的维度是不一样的,你会发现x_norm取得是x中每一行的模,所以x和x_norm的行数是一样的,但是x_norm只有一列.尽管如此吗,在Python运算时,它会自动将x_norm复制,使得x_norm拥有和x一样的维度,这就是Python中的"广播"机制
**Note**:
In normalizeRows(), you can try to print the shapes of x_norm and x, and then rerun the assessment. You'll find out that they have different shapes. This is normal given that x_norm takes the norm of each row of x. So x_norm has the same number of rows but only 1 column. So how did it work when you divided x by x_norm? This is called broadcasting and we'll talk about it now!
广播机制以及softmax函数
### 1.5 - Broadcasting and the softmax function ####
A very important concept to understand in numpy is "broadcasting". It is very useful for performing mathematical operations between arrays of different shapes. For the full details on broadcasting, you can read the official [broadcasting documentation](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html).
练习:使用numpy中的softmax函数
**Exercise**: Implement a softmax function using numpy. You can think of softmax as a normalizing function used when your algorithm needs to classify two or more classes. You will learn more about softmax in the second course of this specialization.
**Instructions**:
- $ \text{for } x \in \mathbb{R}^{1\times n} \text{, } softmax(x) = softmax(\begin{bmatrix}
x_1 &&
x_2 &&
... &&
x_n
\end{bmatrix}) = \begin{bmatrix}
\frac{e^{x_1}}{\sum_{j}e^{x_j}} &&
\frac{e^{x_2}}{\sum_{j}e^{x_j}} &&
... &&
\frac{e^{x_n}}{\sum_{j}e^{x_j}}
\end{bmatrix} $
- $\text{for a matrix } x \in \mathbb{R}^{m \times n} \text{, $x_{ij}$ maps to the element in the $i^{th}$ row and $j^{th}$ column of $x$, thus we have: }$ $$softmax(x) = softmax\begin{bmatrix}
x_{11} & x_{12} & x_{13} & \dots & x_{1n} \\
x_{21} & x_{22} & x_{23} & \dots & x_{2n} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{m1} & x_{m2} & x_{m3} & \dots & x_{mn}
\end{bmatrix} = \begin{bmatrix}
\frac{e^{x_{11}}}{\sum_{j}e^{x_{1j}}} & \frac{e^{x_{12}}}{\sum_{j}e^{x_{1j}}} & \frac{e^{x_{13}}}{\sum_{j}e^{x_{1j}}} & \dots & \frac{e^{x_{1n}}}{\sum_{j}e^{x_{1j}}} \\
\frac{e^{x_{21}}}{\sum_{j}e^{x_{2j}}} & \frac{e^{x_{22}}}{\sum_{j}e^{x_{2j}}} & \frac{e^{x_{23}}}{\sum_{j}e^{x_{2j}}} & \dots & \frac{e^{x_{2n}}}{\sum_{j}e^{x_{2j}}} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
\frac{e^{x_{m1}}}{\sum_{j}e^{x_{mj}}} & \frac{e^{x_{m2}}}{\sum_{j}e^{x_{mj}}} & \frac{e^{x_{m3}}}{\sum_{j}e^{x_{mj}}} & \dots & \frac{e^{x_{mn}}}{\sum_{j}e^{x_{mj}}}
\end{bmatrix} = \begin{pmatrix}
softmax\text{(first row of x)} \\
softmax\text{(second row of x)} \\
... \\
softmax\text{(last row of x)} \\
\end{pmatrix} $$
# GRADED FUNCTION: softmax
"""
def softmax(x):
return np.exp(x)/np.sum(np.exp(x) , axis=1,keepdims=True)
"""
def softmax(x):
"""Calculates the softmax for each row of the input x.
Your code should work for a row vector and also for matrices of shape (n, m).
Argument:
x -- A numpy matrix of shape (n,m)
Returns:
s -- A numpy matrix equal to the softmax of x, of shape (n,m)
"""
### START CODE HERE ### (≈ 3 lines of code)
# Apply exp() element-wise to x. Use np.exp(...).
x_exp = np.exp(x)
# Create a vector x_sum that sums each row of x_exp. Use np.sum(..., axis = 1, keepdims = True).
x_sum = np.sum(np.exp(x),axis=1,keepdims = True)
# Compute softmax(x) by dividing x_exp by x_sum. It should automatically use numpy broadcasting.
s = x_exp / x_sum
### END CODE HERE ###
return s
x = np.array([
[9, 2, 5, 0, 0],
[7, 5, 0, 0 ,0]])
print("softmax(x) = " + str(softmax(x)))
"""
Expected Output:
softmax(x) = [[9.80897665e-01 8.94462891e-04 1.79657674e-02 1.21052389e-04
1.21052389e-04]
[8.78679856e-01 1.18916387e-01 8.01252314e-04 8.01252314e-04
8.01252314e-04]]
"""注意:如果你有在上面的cell里面打印x_exp\x_sum\s的维度的话,你会发现x_sum的维度是(2,1)而x_exp和s的维度则是(2,5) 这就是python中的广播机制在起作用
**Note**:
- If you print the shapes of x_exp, x_sum and s above and rerun the assessment cell, you will see that x_sum is of shape (2,1) while x_exp and s are of shape (2,5). **x_exp/x_sum** works due to python broadcasting.
Congratulations! You now have a pretty good understanding of python numpy and have implemented a few useful functions that you will be using in deep learning.
你需要记住的知识点:
-np.exp(x)适用于任何np.array的数组,并且会对每个x进行取指数的操作
-你需要记住sigmoid函数以及它的梯度下降算式(上方sigmoid( )以及sigmoid_derivative( ))
-深度学习中经常使用图像转二维向量的方法(image2vector)
-np.reshape被广泛使用,在未来的课程里你会发现保证你的矩阵/向量维度正确会少很多bug
-numpy是个十分有用的即用算法
-广播非常有用
<font color='blue'>
**What you need to remember:**
- np.exp(x) works for any np.array x and applies the exponential function to every coordinate
- the sigmoid function and its gradient
- image2vector is commonly used in deep learning
- np.reshape is widely used. In the future, you'll see that keeping your matrix/vector dimensions straight will go toward eliminating a lot of bugs.
- numpy has efficient built-in functions
- broadcasting is extremely useful
第二部分:向量化操作
在深度学习的领域,你会处理非常庞大的数据集.因此无法实现计算优化的函数会成为你深度学习算法的瓶颈,并且会导致你的模型需要花费很长的时间去训练.为了保证你的代码在计算的时候具有高效率,你需要使用到向量化这一操作.具体看下面的计算例子:dot/outer/elementwise
## 2) Vectorization
In deep learning, you deal with very large datasets. Hence, a non-computationally-optimal function can become a huge bottleneck in your algorithm and can result in a model that takes ages to run. To make sure that your code is computationally efficient, you will use vectorization. For example, try to tell the difference between the following implementations of the dot/outer/elementwise product.
import time
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
### CLASSIC DOT PRODUCT OF VECTORS IMPLEMENTATION ###
tic = time.process_time()
dot = 0
for i in range(len(x1)):
dot+= x1[i]*x2[i]
toc = time.process_time()
print ("dot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
### CLASSIC OUTER PRODUCT IMPLEMENTATION ###
tic = time.process_time()
outer = np.zeros((len(x1),len(x2))) # we create a len(x1)*len(x2) matrix with only zeros
for i in range(len(x1)):
for j in range(len(x2)):
outer[i,j] = x1[i]*x2[j]
toc = time.process_time()
print ("outer = " + str(outer) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
### CLASSIC ELEMENTWISE IMPLEMENTATION ###
tic = time.process_time()
mul = np.zeros(len(x1))
for i in range(len(x1)):
mul[i] = x1[i]*x2[i]
toc = time.process_time()
print ("elementwise multiplication = " + str(mul) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
### CLASSIC GENERAL DOT PRODUCT IMPLEMENTATION ###
W = np.random.rand(3,len(x1)) # Random 3*len(x1) numpy array
tic = time.process_time()
gdot = np.zeros(W.shape[0])
for i in range(W.shape[0]):
for j in range(len(x1)):
gdot[i] += W[i,j]*x1[j]
toc = time.process_time()
print ("gdot = " + str(gdot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
"""
Expected Output:
dot = 278
----- Computation time = 0.0ms
outer = [[81. 18. 18. 81. 0. 81. 18. 45. 0. 0. 81. 18. 45. 0. 0.]
[18. 4. 4. 18. 0. 18. 4. 10. 0. 0. 18. 4. 10. 0. 0.]
[45. 10. 10. 45. 0. 45. 10. 25. 0. 0. 45. 10. 25. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[63. 14. 14. 63. 0. 63. 14. 35. 0. 0. 63. 14. 35. 0. 0.]
[45. 10. 10. 45. 0. 45. 10. 25. 0. 0. 45. 10. 25. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[81. 18. 18. 81. 0. 81. 18. 45. 0. 0. 81. 18. 45. 0. 0.]
[18. 4. 4. 18. 0. 18. 4. 10. 0. 0. 18. 4. 10. 0. 0.]
[45. 10. 10. 45. 0. 45. 10. 25. 0. 0. 45. 10. 25. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
----- Computation time = 0.0ms
elementwise multiplication = [81. 4. 10. 0. 0. 63. 10. 0. 0. 0. 81. 4. 25. 0. 0.]
----- Computation time = 0.0ms
gdot = [22.62370613 21.27526358 29.69348931]
----- Computation time = 0.0ms
"""(上面这个计算量太小了,所以时间都是0ms,但实际上向量化和非向量化的时间差距真的很大,可以看下面自己尝试的代码)
import numpy as np
import time
a = np.random.rand(1000000)
b = np.random.rand(1000000)
tic = time.time()
c = np.dot(a,b)
toc = time.time()
print("Vectorized Version " + str(1000 * (toc - tic)) + "ms")
c = 0
tic = time.time()
for i in range(1000000):
c += a[i]*b[i]
toc =time.time()
print("Non-Vectorized Version " + str(1000 * (toc - tic)) + "ms")
"""
Expected Output:
Vectorized Version 0.9887218475341797ms
Non-Vectorized Version 356.17852210998535ms
"""我们发现应用向量化是如此简洁以及效率。对于更大的向量/矩阵而言,运行时间的差距会更大
注意:np.dot()适用于矩阵-矩阵或者矩阵-向量的相乘操作,它是不用于np.multiply()以及*(相当于Matlab/Octave中的.*)操作的,np.multiply()以及*适用行-行相乘
As you may have noticed, the vectorized implementation is much cleaner and more efficient. For bigger vectors/matrices, the differences in running time become even bigger.
**Note** that `np.dot()` performs a matrix-matrix or matrix-vector multiplication. This is different from `np.multiply()` and the `*` operator (which is equivalent to `.*` in Matlab/Octave), which performs an element-wise multiplication.
应用L1以及L2损失函数
### 2.1 Implement the L1 and L2 loss functions
**Exercise**: Implement the numpy vectorized version of the L1 loss. You may find the function abs(x) (absolute value of x) useful.
**Reminder**:
- The loss is used to evaluate the performance of your model. The bigger your loss is, the more different your predictions ($ \hat{y} $) are from the true values ($y$). In deep learning, you use optimization algorithms like Gradient Descent to train your model and to minimize the cost.
- L1 loss is defined as:
$$\begin{align*} & L_1(\hat{y}, y) = \sum_{i=0}^m|y^{(i)} - \hat{y}^{(i)}| \end{align*}\tag{6}$$
# GRADED FUNCTION: L1
"""
def L1(yhat,y):
return np.sum(abs(y -yhat),axis= 0)
"""
def L1(yhat, y):
"""
Arguments:
yhat -- vector of size m (predicted labels)
y -- vector of size m (true labels)
Returns:
loss -- the value of the L1 loss function defined above
"""
### START CODE HERE ### (≈ 1 line of code)
loss = np.sum(abs(y -yhat),axis= 0)
### END CODE HERE ###
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L1 = " + str(L1(yhat,y)))
"""
Expected Output:
L1 = 1.1
"""
**Exercise**: Implement the numpy vectorized version of the L2 loss. There are several way of implementing the L2 loss but you may find the function np.dot() useful. As a reminder, if $x = [x_1, x_2, ..., x_n]$, then `np.dot(x,x)` = $\sum_{j=0}^n x_j^{2}$.
- L2 loss is defined as $$\begin{align*} & L_2(\hat{y},y) = \sum_{i=0}^m(y^{(i)} - \hat{y}^{(i)})^2 \end{align*}\tag{7}$$
"""
def L2(yhat,y):
return np.sum(np.dot((yhat-y).T,(yhat-y)))
"""
# GRADED FUNCTION: L2
def L2(yhat, y):
"""
Arguments:
yhat -- vector of size m (predicted labels)
y -- vector of size m (true labels)
Returns:
loss -- the value of the L2 loss function defined above
"""
### START CODE HERE ### (≈ 1 line of code)
### END CODE HERE ###
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L2 = " + str(L2(yhat,y)))
"""
Expected Output:
L2 = 0.43
"""





















 1879
1879











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








