XGBoost-代码

原创 已于 2023-12-19 20:59:20 修改 · 1.7k 阅读 · 32 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#集成学习 #机器学习

于 2023-12-19 20:56:59 首次发布

介绍

不同于内嵌在sklearn框架中的其他算法，xgboost是独立的算法库，因此它有一套不同于sklearn代码的原生代码。大部分时候我们使用原生代码来运行xgboost，因为这套原生代码是完全为集成学习所设计的，不仅可以无缝使用交叉验证、默认输出指标为RMSE，还能够默认输出训练集上的结果帮我们监控模型。然而对于熟悉sklearn的我们来说，这一套代码略有难度，因此许多人也会倾向于使用xgboost自带的sklearn接口来实现算法。

XGBoost自带sklearn接口（sklearn API），通过这个接口，我们可以使用跟sklearn代码一样的方式来实现xgboost，即可以通过fit和predict等接口来执行训练预测过程，也可以调用属性比如coef_等。在XGBoost的sklearn API中，我们可以看到下面五个类：

类说明
XGBRegressor()实现xgboost回归
XGBClassifier()实现xgboost分类
XGBRanker()实现xgboost排序
XGBRFClassifier()基于xgboost库实现随机森林分类
XGBRFRegressor()基于xgboost库实现随机森林回归

注释：

其中XGBRF的两个类是以XGBoost方式建树、但以bagging方式构建森林的类，通常只有在我们使用普通随机森林效果不佳、但又不希望使用Boosting的时候使用

class xgboost.XGBRegressor(n_estimators, max_depth, learning_rate, verbosity, objective, booster, tree_method, n_jobs, gamma, min_child_weight, max_delta_step, subsample, colsample_bytree, colsample_bylevel, colsample_bynode, reg_alpha, reg_lambda, scale_pos_weight, base_score, random_state, missing, num_parallel_tree, monotone_constraints, interaction_constraints, importance_type, gpu_id, validate_parameters, predictor, enable_categorical, eval_metric, early_stopping_rounds, callbacks,**kwargs)

class xgboost.XGBClassifier(n_estimators, use_label_encoder, max_depth, learning_rate, verbosity, objective, booster, tree_method, n_jobs, gamma, min_child_weight, max_delta_step, subsample, colsample_bytree, colsample_bylevel, colsample_bynode, reg_alpha, reg_lambda, scale_pos_weight, base_score, random_state, missing, num_parallel_tree, monotone_constraints, interaction_constraints, importance_type, gpu_id, validate_parameters, predictor, enable_categorical, **kwargs)

XGBoost回归的sklearn API实现

# 导入sklearn相关的库
from xgboost import XGBRegressor
from sklearn.model_selection import cross_validate, KFold
from sklearn.model_selection import train_test_split

# 读取train_encode数据集
data = pd.read_csv("train_encode.csv",index_col=0)

# 定义特征数据集和标签数据集
X = data.iloc[:,:-1]
y = data.iloc[:,-1]

# 对数据集进行分割，实例化模型，并对数据集进行训练，查看在测试集上的表现情况
#sklearn普通训练代码三步走：实例化，fit，score
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size=0.3,random_state=1412)

xgb_sk = XGBRegressor(random_state=1412) #实例化模型
xgb_sk.fit(Xtrain,Ytrain)
xgb_sk.score(Xtest,Ytest) #默认指标R2

# 对XGBoost回归器进行5折交叉验证，查看在测试集和训练集上的RMSE表现情况
#sklearn交叉验证三步走：实例化，交叉验证，对结果求平均

xgb_sk = XGBRegressor(random_state=1412) #实例化模型

#定义所需的交叉验证方式
cv = KFold(n_splits=5,shuffle=True,random_state=1412)

result_xgb_sk = cross_validate(xgb_sk,X,y,cv=cv
                               ,scoring="neg_root_mean_squared_error" #负根均方误差
                               ,return_train_score=True
                               ,verbose=True
                               ,n_jobs=-1)
result_xgb_sk

def RMSE(result,name):
    return abs(result[name].mean())

RMSE(result_xgb_sk,"train_score")
RMSE(result_xgb_sk,"test_score")

在默认参数下，xgboost模型极度不稳定，并且过拟合的情况非常严重，现有数据量对xgboost来说可能有点不足。在没有调整任何参数的情况下，XGBoost的表现没能胜过梯度提升树，这可能是因为在默认参数下梯度提升树的过拟合程度较轻。我们可以尝试使用之前学过的知识，对XGBoost的参数略微进行调整，例如将最可能影响模型的参数之一：max_depth设置为一个较小的值。

# 实例化深度为5的XGBoost回归器，并对其进行5折交叉验证， 查看测试集和训练集上的RMSE表现情况
xgb_sk = XGBRegressor(max_depth=5,random_state=1412) #实例化
result_xgb_sk = cross_validate(xgb_sk,X,y,cv=cv
                               ,scoring="neg_root_mean_squared_error" #负根均方误差
                               ,return_train_score=True
                               ,verbose=True
                               ,n_jobs=-1)
RMSE(result_xgb_sk,"train_score");RMSE(result_xgb_sk,"test_score")

xgb_sk = XGBRegressor(max_depth=5,random_state=1412).fit(X,y)
# 查看特征重要性
xgb_sk.feature_importances_

# 查看第三棵树的信息
#调出其中一棵树，不过无法展示出树的细节，只能够调出建树的Booster对象
xgb_sk.get_booster()[2]

# 查看一共建立了多少棵树（code）
# 查看一共建立了多少棵树，相当于是n_estimators的取值
xgb_sk.get_num_boosting_rounds()

# 获取每一个参数的取值（code）
xgb_sk.get_params()

XGBoost回归的原生代码实现

注意：

原生代码必须使用XGBoost自定义的数据结构DMatrix，这一数据结构能够保证xgboost算法运行更快，并且能够自然迁移到GPU上运行，类似于列表、数组、Dataframe等结构都不能用于原生代码，因此使用原生代码的第一步就是要更换数据结构。

设置好数据结构后，我们需要以字典形式设置参数。我们往往会使用字典单独呈现参数。准备好参数列表后，我们将使用xgboost中自带的方法xgb.train或xgb.cv进行训练，训练完毕后，我们可以使用predict方法对结果进行预测。虽然xgboost原生代码库所使用的数据结构是DMatrix，但在预测试输出的数据结构却是普通的数组，因此可以直接使用sklearn中的评估指标，或者python编写的评估指标进行评估。

class xgboost.DMatrix(data, label=None, *, weight=None, base_margin=None, missing=None, silent=False, feature_names=None, feature_types=None, nthread=None, group=None, qid=None, label_lower_bound=None, label_upper_bound=None, feature_weights=None, enable_categorical=False)

function xgboost.train(*params, dtrain, num_boost_round=10, *, evals=None, obj=None, feval=None, maximize=None, early_stopping_rounds=None, evals_result=None, verbose_eval=True, xgb_model=None, callbacks=None, custom_metric=None)

function xgboost.cv(*params, dtrain, num_boost_round=10, nfold=3, stratified=False, folds=None, metrics=(), obj=None, feval=None, maximize=None, early_stopping_rounds=None, fpreproc=None, as_pandas=True, verbose_eval=None, show_stdv=True, seed=0, callbacks=None, shuffle=True, custom_metric=None)

注意：

  1. xgb.train和xgb.cv的第一个参数params就是我们需要使用字典自定义的参数列表；
  2. 第二个参数dtrain就是DMatrix结构的训练数据；
  3. 第三个参数num_boost_round其实就等同于sklearn中的n_estimators，表示总共建立多少棵提升树，也就是提升过程中的迭代次数。
# 导入xgboost库
import xgboost as xgb

# 读取train_encode数据集
data = pd.read_csv("train_encode.csv",index_col=0)

# 定义特征数据集和标签数据集
X = data.iloc[:,:-1]
y = data.iloc[:,-1]

# 将上面X和y转化为DMatrix
data_xgb = xgb.DMatrix(X,y)

# 分割训练集和测试集(7-3分），将分割后的数据集转为DMatrix
from sklearn.model_selection import train_test_split
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size=0.3,random_state=1412)
dtrain = xgb.DMatrix(Xtrain,Ytrain)
dtest = xgb.DMatrix(Xtest,Ytest)

注意：

  • DMatrix会将特征矩阵与标签打包在同一个对象中，且一次只能转换一组数据。并且，我们无法通过索引或循环查看内部的内容，一旦数据被转换为DMatrix，就难以调用或修改了；
  • 数据预处理需要在转换为DMatrix之前做好。如果我们有划分训练集和测试集，则需要分别将训练集和测试集转换为DMatrix。
# 定义所需的参数
params = {"max_depth":5,"seed":1412}

# 利用XGBoost对数据进行训练，建立100棵树
reg = xgb.train(params, data_xgb, num_boost_round=100)

注意：

  • XGBoost不需要实例化，xgb.train函数包揽了实例化和训练的功能，XGBoost在训练时没有区分回归和分类器，它默认是执行回归算；
  • xgboost不推荐将参数num_boost_round写在params里，即便现在这样可以运行，但在之后的版本迭代中也会逐渐舍弃这个功能。这既是说，xgboost将参数分为了两大部分，一部分可以通过params进行设置，另一部分则需要在方法xgb.train或者xgb.cv中进行设置。但一般来说，除了建树棵树、提前停止这两个关键元素，其他参数基本都被设置在params当中。
# 利用训练好的模型对数据进行预测，并查看预测数据
y_pred = reg.predict(data_xgb)

# 计算RMSE
from sklearn.metrics import mean_squared_error as MSE
MSE(y,y_pred,squared=False) #RMSE

# 使用交叉验证进行训练
params = {"max_depth":5,"seed":1412}
result = xgb.cv(params,data_xgb,num_boost_round=100
                ,nfold=5 #补充交叉验证中所需的参数，nfold=5表示5折交叉验证
                ,seed=1412 #交叉验证的随机数种子，params中的是管理boosting过程的随机数种子
               )
result
train-rmse-meantrain-rmse-stdtest-rmse-meantest-rmse-std
0141522.7218751318.896997141941.4843756432.947712
1102183.5687501053.673671103857.7531255778.064364
274524.579688728.01914377554.0218755732.164228
355214.231250465.42877659894.9820316121.923227
441754.467188345.49664947824.1140635734.477932
……………
952513.421875206.43297228623.1109387513.194129
962476.676709201.60599928624.6773447517.551419
972440.533399203.69802428620.4683597523.209246
982405.017529210.98320328619.2281257525.503699
992362.659668218.22138328623.2203137526.333222

100 rows × 4 columns

注意：

  • 行数代表迭代次数
  • 每一行代表了每次迭代后进行交叉验证的结果的均值，例如索引为0的行就表示迭代了一次时（刚建立第一棵树时），进行5折交叉验证的结果，最后一行的结果也就是当前模型迭代完毕后（建好了全部的nun_boost_round棵树时）输出的结果，也是之前我们使用sklearn API时得到过的结果：测试集上5折交叉验证结果28623.22

XGBoost分类

原生代码

XGBoost默认会实现回归算法，因此在执行分类的时候，我们需要主动声明算法的类型。xgboost是通过当前算法所使用的损失函数来判断任务类型的，即是通过在params中填写的objective参数来判断任务类型。objective参数中可以输入数十种不同的选项，常见的有：

  • 用于回归
  • reg:squarederror：平方损失，即12(y−y^)2\frac{1}{2}(y - \hat{y})^221​(y−y^​)2，其中1/2是为了计算简便；
  • reg:squaredlogerror：平方对数损失，即12[log(y^+1)−log(y+1)]2\frac{1}{2}[log(\hat{y} + 1) - log(y + 1)]^221​[log(y^​+1)−log(y+1)]2（取log放大差距，常用于金融序列数据），其中1/2是为了计算简便。
  • 用于分类
  • binary:logistic：二分类交叉熵损失，使用该损失时predict接口输出概率。如果你对该损失不熟悉，你需要学习逻辑回归算法；
  • binary:logitraw：二分类交叉熵损失，使用该损失时predict接输出执行sigmoid变化之前的值；
  • multi:softmax：多分类交叉熵损失，使用该损失时predict接口输出具体的类别。如果你对该损失不熟悉，你需要学习AdaBoost与GBD；
  • multi:softprob：多分类交叉熵，适用该损失时predict接口输出每个样本每个类别下的概率。

除此之外，还有众多用于排序算法、计数算法的损失函数。xgboost几乎适用于所有可微的损失函数，不同的损失函数会影响predict的输出，但却不会影响交叉验证方法xgb.cv的输出。当不填写任何内容时，参数objective的默认值为reg:squarederror

  • 导入数据
#导入2个最简单的分类数据集：乳腺癌数据集与手写数字数据集
from sklearn.datasets import load_breast_cancer, load_digits

#二分类数据
X_binary = load_breast_cancer().data
y_binary = load_breast_cancer().target
data_binary = xgb.DMatrix(X_binary,y_binary)

#多分类数据
X_multi = load_digits().data
y_multi = load_digits().target
data_multi = xgb.DMatrix(X_multi, y_multi)
  • 设置params，进行训练
# 在乳腺癌数据集训练xgboost分类器，建立100棵树
params1 = {"seed":1412, "objective":"binary:logistic"#任务类型
           ,"eval_metric":"logloss" #二分类交叉熵损失
          }
clf_binary = xgb.train(params1, data_binary, num_boost_round=100)

# 在手写数据集据集训练xgboost分类器，建立100棵树
params2 = {"seed":1412, "objective":"multi:softmax"#任务类型
           ,"eval_metric":"mlogloss" #多分类交叉熵损失 #"merror"
           ,"num_class":10}
clf_multi = xgb.train(params2, data_multi, num_boost_round=100)

注意：

  • 相比起默认的回归算法，xgboost分类算法所需的参数会更多一些。二分类损失函数一般需要搭配参数eval_matric，用于设置分类的评估指标。xgboost中默认的二分类指标是对数损失（也就是交叉熵损失logloss）；
  • 对多分类算法来说，除了设置损失函数和评估指标，还需要设置参数num_class。参数num_class用于多分类状况下、具体的标签类别数量。通常来说，算法应该能够根据标签的情况自主判断实际类别为多少
  • 预测与评估
# 利用训练好的二分类和多分类xgboost对数据集进行预测
y_pred_binary = clf_binary.predict(data_binary)
y_pred_multi = clf_multi.predict(data_multi)

# 导入评估指标函数
from sklearn.metrics import accuracy_score as ACC #当返回具体类别时，可以使用准确率
from sklearn.metrics import log_loss as logloss #当返回概率时，则必须使用交叉熵损失
#  Loss = -(y * log (p) + (1 - y) * log (1 - p))

# 计算对于两个数据集预测的效果
ACC(y_binary,(y_pred_binary > 0.5).astype(int)) #对二分类计算准确率，则必须先转换为类别
ACC(y_multi, y_pred_multi)

# 查看交叉熵损失
logloss(y_binary,y_pred_binary) #只有二分类输出了概率，因此可以查看交叉熵损失
  • 交叉验证
# 用xgboost对手写数字数据集DMatrix进行5折交叉验证，建立100棵树，评估指标采用mlogloss和merror（code）
params3 = {"seed":1412
           , "objective":"multi:softmax" #无论填写什么损失函数都不影响交叉验证的评估指标
           , "num_class":10}
result = xgb.cv(params3,data_multi,num_boost_round=100
                ,metrics = ("mlogloss","merror")
                # merror:多类别分类问题中的分类错误率
                ,nfold=5 #补充交叉验证中所需的参数，nfold=5表示5折交叉验证
                ,seed=1412 #交叉验证的随机数种子，params中的是管理boosting过程的随机数种子
               )
result
train-mlogloss-meantrain-mlogloss-stdtrain-merror-meantrain-merror-stdtest-mlogloss-meantest-mlogloss-stdtest-merror-meantest-merror-std
01.2289120.0061920.0307460.0026581.3303490.0393770.1229780.022670
10.8692810.0059740.0143290.0039481.0093040.0466650.0940410.022593
20.6427090.0055210.0087650.0027320.8057010.0502070.0806820.022009
30.4842230.0045900.0051470.0014320.6584860.0494340.0706640.022264
40.3703310.0042050.0032000.0013620.5526570.0490020.0651010.018976
………………………
950.0039210.0000270.0000000.0000000.1181050.0279680.0383920.005910
960.0039080.0000260.0000000.0000000.1180070.0278990.0383920.005910
970.0038960.0000260.0000000.0000000.1180730.0279420.0383920.005910
980.0038850.0000260.0000000.0000000.1179760.0279110.0383920.005910
990.0038740.0000260.0000000.0000000.1177790.0279600.0383920.005910

100 rows × 8 columns

当使用xgb.train时，我们会将评估指标参数eval_matric写在params中，在使用xgb.cv时，我们却需要将评估指标参数写在xgb.cv当中,在xgb.cv当中，我们需要将评估指标打包成元组，写在参数metrics内部

sklearn API

# 导入XGBoost分类器
from xgboost import XGBClassifier

# 实例化XGBoost分类器，查看分类器的所有参数取值
clf = XGBClassifier()
clf.get_params()

# 实例化多分类XGBoost分类器，类被为10，并对手写数据集数据进行训练，查看预测数值、概率和得分
clf = XGBClassifier(objective="multi:softmax"
                    , eval_metric="mlogloss" #设置评估指标避免警告
                    , num_class = 10
                  #  , use_label_encoder=False
                   ) 
clf = clf.fit(X_multi,y_multi)
clf.predict(X_multi) #输出具体数值 - 具体的预测类别
clf.predict_proba(X_multi).shape #输出概率值
clf.score(X_multi,y_multi) #虽然设置了评估指标，但score接口还是准确率

XGBoost的参数

类型参数
迭代过程/目标函数num_boost_round：集成算法中弱分类器数量，对Boosting算法而言为实际迭代次数

eta：Boosting算法中的学习率，影响弱分类器结果的加权求和过程

objective：选择需要优化的损失函数

base_score：初始化预测结果H0H_0H0​的设置

max_delta_step：一次迭代中所允许的最大迭代值

gamma：乘在叶子数量前的系数，放大可控制过拟合

lambda：L2正则项系数，放大可控制过拟合

alpha：L1正则项系数，放大可控制过拟合
弱评估器结构（DART）booster：选择迭代过程中的弱评估器类型，包括gbtree，DART和线性模型

sample_type：DART树中随机抽样树的具体方法

rate_drop：DART树中所使用的抛弃率

one_drop：每轮迭代时至少需要抛弃的树的数量

skip_drop：在迭代中不进行抛弃的概率

normalized_type：根据被抛弃的树的权重控制新增树权重

max_depth：允许的弱评估器的最大深度

min_child_weight：（广义上）叶子节点上的最小样本权重/最小样本量

gamma：目标函数中叶子数量TTT的系数，同时也是分枝时所需的最小结构分数增益值

lambda与alpha：正则项系数，同时也位于结构分数的公式中，间接影响模型的剪枝

弱评估器的训练数据sampling_method：对样本进行抽样具体方式

subsample：对样本进行抽样的具体比例

colsample_bytree, colsample_bylevel, colsample_bynode：在建树过程中对特征进行抽样的比例
提前停止xgb.train(): early_stopping_rounds, evals, eval_metric
其他params: seed, verbosity, scale_pos_weight, nthread

  • 迭代过程

    • eta:Hk(xi)=Hk−1(xi)+ηfk(xi)H_k(x_i) = H_{k-1}(x_i) + \boldsymbol{\color{red}\eta} f_k(x_i)Hk​(xi​)=Hk−1​(xi​)+ηfk​(xi​)

      当学习率很大时，H(xi)H(x_i)H(xi​)增长得更快，我们所需的num_boost_round更少，当学习率较小时，H(xi)H(x_i)H(xi​)增长较慢，我们所需的num_boost_round就更多，因此boosting算法往往会需要在num_boost_round与eta中做出权衡。在XGBoost当中，num_boost_round的默认值为10，eta的默认值为0.3.

    • base_score:第0棵树

      在xgboost中，我们可以对base_score输出任何数值，但并不支持类似于GBDT当中输入评估器的操作。当不填写时，该参数的默认值为0.5，即对所有样本都设置0.5为起始值。当迭代次数足够多、数据量足够大时，调整算法的H0(xi)H_0(x_i)H0​(xi​)意义不大，因此我们基本不会调整这个参数。

    • max_delta_step:代表了每次迭代时被允许的最大ηfk(xi)\eta f_k(x_i)ηfk​(xi​)

      当参数max_delta_step被设置为0，则说明不对每次迭代的ηfk(xi)\eta f_k(x_i)ηfk​(xi​)大小做限制，如果该参数被设置为正数C，则代表ηfk(xi)≤C\eta f_k(x_i) \leq Cηfk​(xi​)≤C，否则就让算法执行：

      Hk(xi)=Hk−1(xi)+CH_k(x_i) = H_{k-1}(x_i) + CHk​(xi​)=Hk−1​(xi​)+C

      通常来说这个参数是不需要的，但有时候这个参数会对极度不均衡的数据有效。如果样本极度不均衡，那可以尝试在这个参数中设置1~10左右的数。

    总结：

    参数含义原生代码sklearn API
    迭代次数/树的数量num_boost_round
    (xgb.train)    		n_estimators
    学习率eta
    (params)    		learning_rate
    初始迭代值base_score
    (params)    		base_score
    一次迭代中所允许的最大迭代值max_delta_step
    (params)    		max_delta_step

  • 目标函数

    需要注意的是，损失函数可以针对单个样本进行计算，也可以针对整个算法进行计算，但在XGBoost的定义(xgboost向着令目标函数最小化的方向运行 )中，目标函数是针对每一棵树的，而不是针对一个样本或整个算法 。对任意树fkf_kfk​来说，目标函数有两个组成部分，一部分是任意可微的损失函数，它控制模型的经验风险。从数值上来说，它等于现在树上所有样本上损失函数之和，其中单一样本的损失为l(yi,yi^)l(y_i,\hat{y_i})l(yi​,yi​^​)。另一部分是控制模型复杂度的Ω(fk)\Omega(f_k)Ω(fk​)，它控制当前树的结构风险。

    Objk=∑i=1Ml(yi,yi^)+Ω(fk)Obj_k = \sum_{i=1}^Ml(y_i,\hat{y_i}) + \Omega(f_k)Objk​=∑i=1M​l(yi​,yi​^​)+Ω(fk​)

    其中MMM表示现在这棵树上一共使用了M个样本，lll表示单一样本的损失函数。当模型迭代完毕之后，最后一棵树上的目标函数就是整个XGBoost算法的目标函数。

    • 经验风险：模型对数据学习越深入，损失越小（经验风险越小），模型对数据学习得越浅显，损失越大（经验风险越大）。

    • 结构风险：树结构越复杂、模型复杂度越高，过拟合风险越大（结构风险越大）;树模型结构越简单、模型复杂度越低、过拟合风险越小（结构风险越小）。

    在具体的公式当中，结构风险Ω(fk)\Omega(f_k)Ω(fk​)又由两部分组成，一部分是控制树结构的γT\gamma TγT，另一部分则是正则项：

    Objk=∑i=1Ml(yi,yi^)+γT+12λ∑j=1Twj2+α∑j=1TwjObj_k = \sum_{i=1}^Ml(y_i,\hat{y_i}) + \boldsymbol{\color{red}\gamma} T + \frac{1}{2}\boldsymbol{\color{red}\lambda}\sum_{j=1}^Tw_j^2 + \boldsymbol{\color{red}\alpha}\sum_{j=1}^Tw_jObjk​=i=1∑M​l(yi​,yi​^​)+γT+21​λj=1∑T​wj2​+αj=1∑T​wj​

    • TTT表示当前第kkk棵树上的叶子总数
    • wjw_jwj​则代表当前树上第jjj片叶子的叶子权重（leaf weights）。叶子权重是XGBoost数学体系中非常关键的一个因子，它实际上就是当前叶子jjj的预测值，这一指标与数据的标签量纲有较大的关系，因此当标签的绝对值较大、wjw_jwj​值也会倾向于越大。因此正则项有两个：使用平方的L2正则项与使用绝对值的L1正则项

    • 参数gamma：

      • 乘在一棵树的叶子总量TTT之前，依照叶子总量对目标函数施加惩罚的系数，默认值为0，可填写任何[0, ∞]之间的数字。因此调大gamma可以控制过拟合。

      • 允许分枝的最低结构分数增益。当分枝时结构增益不足gamma中设置的值，该节点被剪枝。gamma在剪枝中的作用就相当于sklearn中的min_impurity_decrease

        Gain=12(ScoreL+ScoreR−ScoreP)−γ=12((∑i∈Lgi)2∑i∈Lhi+λ+(∑i∈Rgi)2∑i∈Rhi+λ−(∑i∈Pgi)2∑i∈Phi+λ)−γ>0\begin{align} Gain &= \frac{1}{2} ( Score_L + Score_R - Score_P ) - \gamma \\ \\ &= \frac{1}{2} \left( \frac{(\sum_{i \in L}g_i)^2}{\sum_{i \in L}h_i + \lambda} + \frac{(\sum_{i \in R}g_i)^2}{\sum_{i \in R}h_i + \lambda} - \frac{(\sum_{i \in P}g_i)^2}{\sum_{i \in P}h_i + \lambda} \right) - \gamma>0 \end{align}Gain​=21​(ScoreL​+ScoreR​−ScoreP​)−γ=21​(∑i∈L​hi​+λ(∑i∈L​gi​)2​+∑i∈R​hi​+λ(∑i∈R​gi​)2​−∑i∈P​hi​+λ(∑i∈P​gi​)2​)−γ>0​​

        因此：12((∑i∈Lgi)2∑i∈Lhi+λ+(∑i∈Rgi)2∑i∈Rhi+λ−(∑i∈Pgi)2∑i∈Phi+λ)>γ\frac{1}{2} \left( \frac{(\sum_{i \in L}g_i)^2}{\sum_{i \in L}h_i + \lambda} + \frac{(\sum_{i \in R}g_i)^2}{\sum_{i \in R}h_i + \lambda} - \frac{(\sum_{i \in P}g_i)^2}{\sum_{i \in P}h_i + \lambda} \right) > \gamma21​(∑i∈L​hi​+λ(∑i∈L​gi​)2​+∑i∈R​hi​+λ(∑i∈R​gi​)2​−∑i∈P​hi​+λ(∑i∈P​gi​)2​)>γ

    • 参数alpha与lambda

      • 乘在正则项之前，依照叶子权重的大小对目标函数施加惩罚的系数，也就是正则项系数。lambda的默认值为1，alpha的默认值为0，因此xgboost默认使用L2正则化。通常来说，我们不会同时使用两个正则化。因此调大alpha或lambda可以控制过拟合。

      • 也位于结构分数中间接影响树的生长和分枝

        当使用L2正则化时，结构分数为：


        Scorej=(∑i∈jgi)2∑i∈jhi+λ Score_j = \frac{(\sum_{i \in j}g_i)^2}{\sum_{i \in j}h_i + \lambda}Scorej​=∑i∈j​hi​+λ(∑i∈j​gi​)2​

        然而，当使用L1正则化时，结构分数为：


        Scorej=(∑i∈jgi+α)2∑i∈jhi Score_j = \frac{(\sum_{i \in j}g_i+ \alpha)^2 }{\sum_{i \in j}h_i}Scorej​=∑i∈j​hi​(∑i∈j​gi​+α)2​

        在XGBoost当中，我们可以同时使用两种正则化，则结构分数为：


        Scorej=(∑i∈jgi+α)2∑i∈jhi+λ Score_j = \frac{(\sum_{i \in j}g_i+ \alpha)^2 }{\sum_{i \in j}h_i + \lambda}Scorej​=∑i∈j​hi​+λ(∑i∈j​gi​+α)2​
        因此，当lambda越大，结构分数Score会越小，参数gamma的力量会被放大(在obj整个式子的比重会变大），模型整体的剪枝会变得更加严格（后一项是γT\gamma TγT），同时，由于lambda还可以通过目标函数(在原始目标函数中是正则化系数）将模型学习的重点拉向结构风险，因此lambda具有双重扛过拟合能力。
        然而，当alpha越大时，结构分数会越大，参数gamma的力量会被缩小，模型整体的剪枝会变得更宽松。然而，alpha还可以通过目标函数将模型学习的重点拉向结构风险，因此alpha会通过放大结构分数抵消一部分扛过拟合的能力(削弱gamma剪枝的效果）。整体来看，alpha是比lambda更宽松的剪枝方式。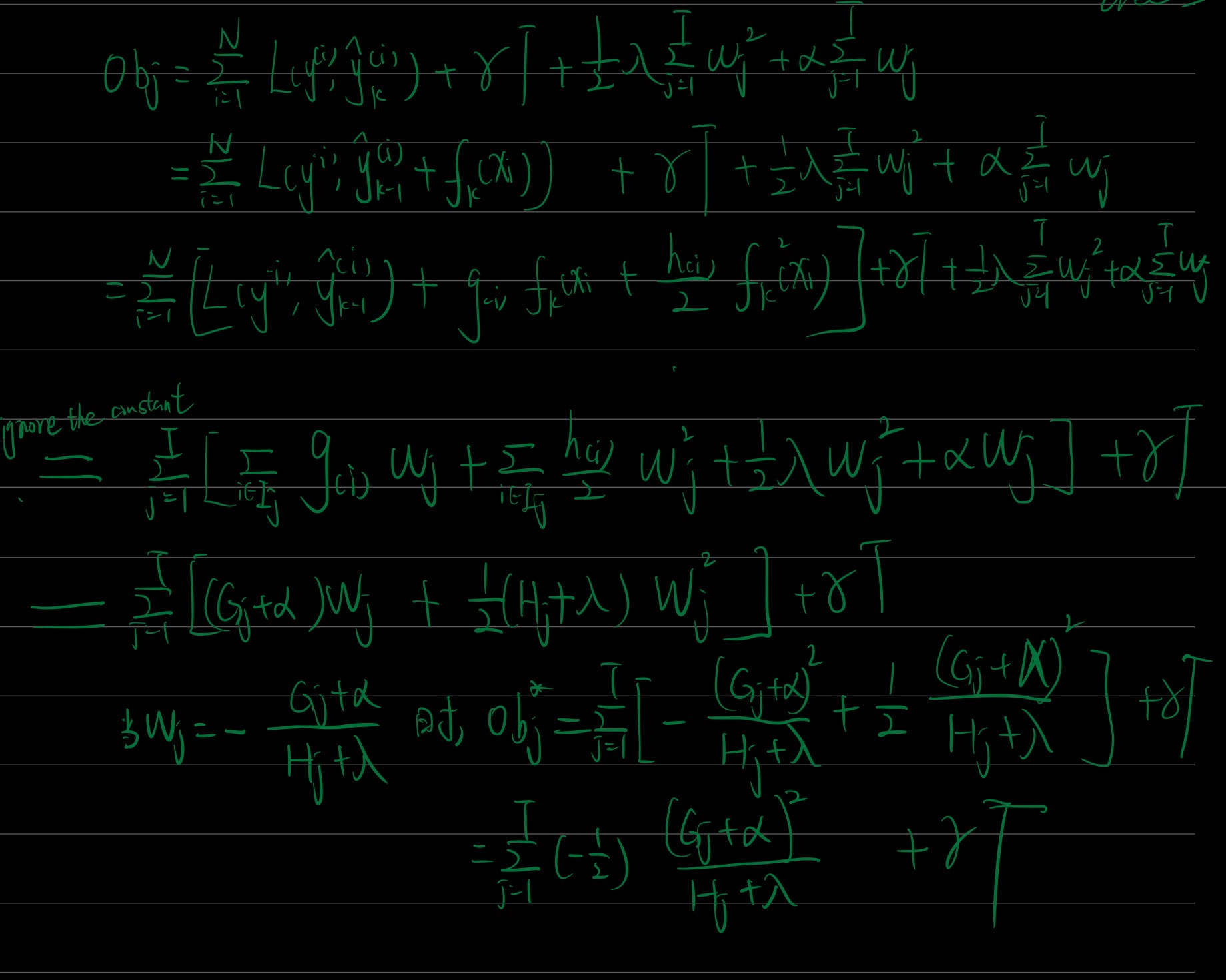
        微信图片_20231207214405

参数含义原生代码sklearn API
乘在叶子节点数量前的系数；允许分枝的最低结构分数增益gamma
(params)		gamma
L2正则项系数；结构分数中间接影响树的生长和分枝lambda
(params)		reg_lambda
L1正则项系数；结构分数中间接影响树的生长和分枝alpha
(params)		reg_alpha

在实际控制过拟合的过程中，大家可能经常会发现这几个参数“无效”。比如我们可以看到：

import xgboost as xgb

# 读取train_encode数据集
data = pd.read_csv("train_encode.csv",index_col=0)


# 定义特征数据集和标签数据集
X = data.iloc[:,:-1]
y = data.iloc[:,-1]

#定义一个函数，用来检测模型迭代完毕后的过拟合情况
def overfitcheck(result):
    return (result.iloc[-1,2] - result.iloc[-1,0]).min()

# 可视化xgboost在参数空间为max_depth=5, 随机种子为1412， 学习率为0.1， 叶子数量的惩罚项为【0，1】，步长为1，进行5折交叉验证下的100次迭代的折线图

train = []
test = []
gamma = np.arange(0,10,1)
overfit = []
for i in gamma:
    params = {"max_depth":5,"seed":1412,"eta":0.1
              ,"gamma":float(i)
             }
    result = xgb.cv(params,data_xgb,num_boost_round=100
                ,nfold=5 #补充交叉验证中所需的参数，nfold=5表示5折交叉验证
                ,seed=1412 #交叉验证的随机数种子，params中的是管理boosting过程的随机数种子
               )
    overfit.append(overfitcheck(result))
    train.append(result.iloc[-1,0])
    test.append(result.iloc[-1,2])
plt.plot(gamma,overfit);

download

# 可视化gamma与训练集的折线图
plt.plot(gamma,train);

屏幕截图 2023-12-07 124230

**对于没有上限或下限的参数，我们要关注参数的敏感度。**如果参数值稍稍移动，模型就变化很大，那参数敏感，如果参数值移动很多，模型才能有变化，那参数不敏感。当树的结构相对复杂时，gamma会比敏感，否则gamma可能非常迟钝

分析（从逆命题来思考）：如果树结构本身不复杂：即树比较浅，分支较少，增加gamma值可能不会对现有的简单结构产生太大影响，因为即使在更高的gamma值下，当前的分支可能仍然是成本效益上合理的。在这种情况下，gamma的变化对模型影响不大，因此是一个不敏感的参数）。

当原始标签数值很大、且叶子数量不多时，lambda和alpha就会敏感，如果原始标签数值很小，这两个参数就不敏感。因此在使用这些参数之前，最好先对参数的敏感程度有一个探索y.describe()

分析：当原始标签数值很大时，模型需要更精细地调整其预测，以准确反映这些较大的数值。在这种情况下，正则化参数对模型性能的影响会更加显著，因为它们控制着模型的复杂性和拟合能力。如果叶子数量不多，这意味着模型本身较为简单，因此正则化参数的调整会对模型产生较大的影响；另一方面，如果原始标签数值较小，模型不需要非常精细的调整来适应这些数值，因此lambda和alpha的调整可能对模型的性能影响不大。即使增加正则化程度，模型可能仍然能够合理地拟合这些较小的数值。

  • 弱评估器结构

    • min_child_weight:任意节点jjj上所允许的最小的∑i∈jhi\sum_{i \in j}h_i∑i∈j​hi​值

      如果一个节点上的∑i∈jhi\sum_{i \in j}h_i∑i∈j​hi​小于该参数中设置的值，该节点被剪枝。

      Scorej=(∑i∈jgi)2∑i∈jhi+λ Score_j = \frac{(\sum_{i \in j}g_i)^2}{\sum_{i \in j}h_i + \lambda}Scorej​=∑i∈j​hi​+λ(∑i∈j​gi​)2​

      其中，hih_ihi​是样本iii的损失函数lll在预测值f(xi)f(x_i)f(xi​)上的二阶导数，∑i∈jhi\sum_{i \in j}h_i∑i∈j​hi​就是该节点上所有样本的hih_ihi​之和。

      在上一节中，假设损失函数为12MSE\frac{1}{2}MSE21​MSE，我们推导出任意样本的hi=1h_i = 1hi​=1，因此∑i∈jhi\sum_{i \in j}h_i∑i∈j​hi​应该等于该叶子节点上的总样本量。因为这个原因，hih_ihi​在XGBoost原始论文和官方说明中有时被称为“样本权重”（instance weight）。因此，当MSE为损失函数时，参数min_child_weight很类似于sklearn中的min_sample_leaf，即一个节点上所允许的最小样本量。


      然而，如果我们使用的损失函数不是MSE，那hih_ihi​也就不会等于1了。不过官方依然将hih_ihi​称之为样本权重，当损失函数更换时，样本的权重也随之变化。当损失函数不为MSE时，参数min_child_weight时一个节点上所允许的最小样本权重量。
      很显然，参数min_child_weight越大，模型越不容易过拟合，同时学习能力也越弱

    • booster:使用哪种弱评估器

      可以输入"gbtree"、“gblinear"或者"dart”。

      输入"gbtree"表示使用遵循XGBoost规则的CART树，我们之前提到的XGBoost在GBDT上做出的改善基本都是针对这一类型的树。这一类型的树又被称为“XGBoost独有树”，XGBoost Unique Tree。

      输入"dart"表示使用抛弃提升树，DART是Dropout Multiple Additive Regression Tree的简称。这种建树方式受深度学习中的Dropout技巧启发，在建树过程中会随机抛弃一些树的结果，可以更好地防止过拟合。在数据量巨大、过拟合容易产生时，DART树经常被使用，但由于会随机地抛弃到部分树，可能会伤害模型的学习能力，同时可能会需要更长的迭代时间。

      输入"gblinear"则表示使用线性模型，当弱评估器类型是"gblinear"而损失函数是MSE时，表示使用xgboost方法来集成线性回归。当弱评估器类型是"gblinear"而损失函数是交叉熵损失时，则代表使用xgboost来集成逻辑回归。

      每一种弱评估器都有自己的params列表，例如只有树模型才会有学习率等参数，只有DART树才会有抛弃率等参数。评估器必须与params中的参数相匹配，否则一定会报错。其中，由于DART树是从gbtree的基础上衍生而来，因此gbtree的所有参数DART树都可以使用。

      参数含义原生代码sklearn API
      选择使用不同的弱评估器booster
      (params)      		booster

DART Booster 介绍

XGBoost 基本上都是组合大量小学习率的回归树。在这种情况, 越晚添加的树比越早添加的树更重要。

  • 特征

    • Drop Trees是为了解决过拟合

    • 因为随机dropout不使用用于保存预测结果的buffer（保证内存连续）所以训练会更慢

    • 因为随机, 早停可能不够稳定

  • DART算法和MART(GBDT)算法主要有两个不同点:

    • dropout
      计算下一棵树要拟合的梯度的时候, 仅仅随机从已经生成的树中选取一部分。假设经过 nnn 次迭代之后当前模型为 M,M=∑i=1nTiM, M=\sum_{i=1}^n T_iM,M=∑i=1n​Ti​, 当中 TiT_iTi​ 是第 iii 次学习到的树。DART算法首先选择一个随机子集 I⊂{1,…,n}I \subset\{1, \ldots, n\}I⊂{1,…,n}, 创建模型 M^=∑i∈ITi\hat{M}=\sum_{i \in I} T_iM^=∑i∈I​Ti​ 。树 TTT 从 {(x,−Lx′(M^(x)))}\left\{\left(x,-L_x^{\prime}(\hat{M}(x))\right)\right\}{(x,−Lx′​(M^(x)))} 学习得到, 当中 Lx′()L_x^{\prime}()Lx′​() 表示求损失函数的梯度作为下一次的标签, GDBT中使用损失函数的梯度作为下一个树的输入标签。
    • 归一化
      DART和MART第二点不同就是DART添加一棵树时需要先归一化。归一化背后的原理是: 树T是尝试减少 M^\hat{M}M^ 和最优预测器之间的差距, dropped trees也是为了减少这个差距。因此引入 new tree和 dropped trees都是为了达到相同的目标。进一步说, 假设通过 III 建立模型 M^\hat{M}M^ 时drop掉k棵树。因此, DART算法将树 TTT 乘以 1/(k+1)1 / (k+1)1/(k+1), 因为不丢弃k棵树而直接产生新树的话，我们迭代更新出来的提升树所需要计算的负梯度是只需要计算新树所需的k+1倍，为了抵消这个差距，需要乘上一个正则化因子 1/(k+1)1 / (k+1)1/(k+1)，对于被丢弃的树要乘k/(k+1)k / (k+1)k/(k+1)，是为了保证新的树的引入和不引入的效果一样（使得每棵树的权重都是11+k\frac{1}{1+k}1+k1​,使得和为1）。

  • 算法流程

    • 在第m次训练, 假设 kkk 棵树被dropped。
    • 假设 D=∑i∈KFiD=\sum_{i \in \mathbf{K}} F_iD=∑i∈K​Fi​ 是dropped trees叶子节点的得分, Fm=ηF~mF_m=\eta \tilde{F}_mFm​=ηF~m​ 是新的树的叶子节点的得分, η\etaη 表示学习率
    • 目标函数如下:
      Obj=∑j=1nL(yj,y^jm−1−D+ηF~m)+Ω(Fm) \mathrm{Obj}=\sum_{j=1}^n L\left(y_j, \hat{y}_j^{m-1}-D+\eta \tilde{F}_m\right)+\Omega\left(F_m\right) Obj=j=1∑n​L(yj​,y^​jm−1​−D+ηF~m​)+Ω(Fm​)

    由于dropout 在设定目标函数时引入了随机丢弃，因此如果直接引入 F~m\tilde{F}_mF~m​ ，则会引起超调。因此引入缩放因子，这称作为归一化

    注意：

    超调通常指的是在优化过程中，参数更新过于激进导致优化目标函数过度变化，可能会导致学习过程不稳定，甚至发散。在梯度下降中，如果学习率过高，那么参数更新可能会超过最优点，导致损失函数在最优值附近来回震荡或者越过最小值点变得更糟。

    • DDD 和 FmF_mFm​ 有相同的目标：缩小预测差距, 使用拉伸系数(scale factor):

      y^jm=∑i∉KFi+a(∑i∈KFi+bFm)\hat{y}_j^m=\sum_{i \notin \mathbf{K}} F_i+a\left(\sum_{i \in \mathbf{K}} F_i+b F_m\right)y^​jm​=∑i∈/K​Fi​+a(∑i∈K​Fi​+bFm​)

      令 F^=∑i≠KFi\hat{F}=\sum_{i \neq \mathbb{K}} F_iF^=∑i=K​Fi​ 。采用归一化的原因是： F~m\tilde{F}_mF~m​ 试图缩小 M^\hat{M}M^ 到目标之间的 gap；而 D\mathrm{D}D也会试图缩小 M^\hat{M}M^ 到目标之间的gap。如果同时引入随机丟弃的子树集合 D\mathrm{D}D ，以及新的子树 FmF_mFm​ ，则会引起超调。

      归一化算法的类型（normalize_type)

      • normalize_type =tree

        • 新的tree和每一个dropped trees有同样的权重

        • 新的trees的权重为 1 / ( k+k+k+ learning_rate)

        • dropped trees乘以一个系数 k/(k+\mathrm{k} /(\mathrm{k}+k/(k+ learning_rate )

          证明：
          a(∑i∈KFi+1kFm)=a(∑i∈KFi+ηkF~m)∼a(1+ηk)D=ak+ηkD=Da=kk+η. \begin{aligned} a\left(\sum_{i \in \mathbf{K}} F_i+\frac{1}{k} F_m\right) & =a\left(\sum_{i \in \mathbf{K}} F_i+\frac{\eta}{k} \tilde{F}_m\right) \\ & \sim a\left(1+\frac{\eta}{k}\right) D \\ & =a \frac{k+\eta}{k} D=D \\ & a=\frac{k}{k+\eta} . \end{aligned} a(i∈K∑​Fi​+k1​Fm​)​=a(i∈K∑​Fi​+kη​F~m​)∼a(1+kη​)D=akk+η​D=Da=k+ηk​.​

      • normalize_type =forest :

        • 新的树和所有dropped trees的和有相同的权重

        • 新的trees的权重为 1 / ( 1+1+1+ learning_rate )))

        • dropped trees乘以一个系数 1/(1+1 /(1+1/(1+ learning_rate )))

          证明：
          a(∑i∈KFi+Fm)=a(∑i∈KFi+ηF~m)∼a(1+η)D=a(1+η)D=Da=11+η. \begin{aligned} a\left(\sum_{i \in \mathbf{K}} F_i+F_m\right) & =a\left(\sum_{i \in \mathbf{K}} F_i+\eta \tilde{F}_m\right) \\ & \sim a(1+\eta) D \\ & =a(1+\eta) D=D \\ & a=\frac{1}{1+\eta} . \end{aligned} a(i∈K∑​Fi​+Fm​)​=a(i∈K∑​Fi​+ηF~m​)∼a(1+η)D=a(1+η)D=Da=1+η1​.​

  • DART 树

    在第kkk次迭代中建立新的树时，迭代后的结果等于之前所有k−1{k-1}k−1棵树的结果加新建立的树的结果:

    Hk(xi)=Hk−1(xi)+ηfk(xi)H_k(x_i) = H_{k-1}(x_i) + \boldsymbol{\color{red}\eta} f_k(x_i)Hk​(xi​)=Hk−1​(xi​)+ηfk​(xi​)

    DART树在每一次迭代前都会随机地抛弃部份树，即不让这些树参与Hk−1(xi)H_{k-1}(x_i)Hk−1​(xi​)的计算，这种随机放弃的方式被叫做“Dropout”（抛弃）。举例说明，假设现在一共有5棵树，结果分别如下：

    k=1k=2k=3k=4k=5
    ηfk(xi)\eta f_k(x_i)ηfk​(xi​)10.80.60.50.3

    当建立第6棵树时，普通提升树的Hk−1(xi)H_{k-1}(x_i)Hk−1​(xi​) = 1+0.8+0.6+0.5+0.3 = 3.2。对于DART树来说，我们可以认为设置抛弃率rate_drop，假设抛弃率为0.2，则DART树会随机从5棵树中抽样一棵树进行抛弃。假设抛弃了第二棵树，则DART树的Hk−1(xi)H_{k-1}(x_i)Hk−1​(xi​) = 1+0.6+0.5+0.3 = 2.4。通过影响Hk−1(xi)H_{k-1}(x_i)Hk−1​(xi​)，DART树影响损失函数、影响整个算法的输出结果H(x)H(x)H(x)，以此就可以在每一次迭代中极大程度地影响整个xgboost的方向。

    在一般的抗过拟合方法当中，我们只能从单棵树的学习能力角度入手花式对树进行剪枝，但DART树的方法是对整体迭代过程进行控制。在任意以“迭代”为核心的算法当中，我们都面临同样的问题，即最开始的迭代极大程度地影响整个算法的走向，而后续的迭代只能在前面的基础上小修小补。在这个过程中，没有任何过抗拟合手段可以从流程上影响到那些先建立的、具有巨大影响力的树，但DART树就可以削弱这些前端树的影响力，大幅提升抗过拟合的能力。

    • 参数rate_drop：每一轮迭代时抛弃树的比例

      设置为0.3，则表示有30%的树会被抛弃。只有当参数booster="dart"时能够使用，只能填写[0.0,1.0]之间的浮点数，默认值为0。

      • 参数one_drop：每一轮迭代时至少有one_drop棵树会被抛弃

        可以设置为任意正整数，例如one_drop = 10，则意味着每轮迭代中至少有10棵树会被抛弃。


        当参数one_drop的值高于rate_drop中计算的结果时，则按照one_drop中的设置执行Dropout。例如，总共有30棵树，rate_drop设置为0.3，则需要抛弃9棵树。但one_drop中设置为10，则一定会抛弃10棵树。当one_drop的值低于rate_drop的计算结果时，则按rate_drop的计算结果执行Dropout。（哪个高执行哪个）

      • 参数skip_drop：每一轮迭代时可以不执行dropout的概率

        即便参数booster=‘dart’，每轮迭代也有skip_drop的概率可以不执行Dropout，是所有设置的概率值中拥有最高权限的参数。该参数只能填写[0.0,1.0]之间的浮点数，默认值为0。当该参数为0时，则表示每一轮迭代都一定会抛弃树。如果该参数不为0，则有可能不执行Dropout，直接按照普通提升树的规则建立新的提升树。


        需要注意的是**，skip_drop的权限高于one_drop。即便one_drop中有所设置，例如每次迭代必须抛弃至少10棵树，但只要skip_drop不为0，每轮迭代则必须经过skip_drop的概率筛选**。如果skip_drop说本次迭代不执行Dropout，则忽略one_drop中的设置。

      • 参数sample_type：抛弃时所使用的抽样方法

        填写字符串"uniform"：表示均匀不放回抽样。


        填写字符串"weighted"：表示按照每棵树的权重进行有权重的不放回抽样。


        注意，该不放回是指在一次迭代中不放回。每一次迭代中的抛弃是相互独立的，因此每一次抛弃都是从所有树中进行抛弃。上一轮迭代中被抛弃的树在下一轮迭代中可能被包括。

      • 参数normalize_type：增加新树时，赋予新树的权重

        当随机抛弃已经建好的树时，可能会让模型结果大幅度偏移，因此往往需要给与后续的树更大的权重，让新增的、后续的树在整体算法中变得更加重要。所以DART树在建立新树时，会有意地给与后续的树更大的权重。我们有两种选择：


        填写字符串"tree"，表示新生成的树的权重等于所有被抛弃的树的权重的均值。


        填写字符串"forest"，表示新生成的树的权重等于所有被抛弃的树的权重之和。

        注意：

        算法默认为"tree"，当我们的dropout比例较大，且我们相信希望给与后续树更大的权重时，会选择"forest"模式。

        注意：两个参数sample_type与normalize_type都使用了概念“树的权重”，树的权重其实指的是整棵树上所有叶子权重之和**

      • DART树的缺点

        • 用于微调模型的一些树可能被抛弃，微调可能失效；
        • 由于存在随机性，模型可能变得不稳定，因此提前停止等功能可能也会变得不稳定；
        • 由于要随机抛弃一些树的结果，在工程上来说就无法使用每一轮之前计算出的Hk−1H_{k-1}Hk−1​，而必须重新对选中的树结果进行加权求和，可能导致模型迭代变得略微缓慢。

      DART树代码

      # xgboost在参数空间为max_depth=5, 随机种子为1412， 学习率为0.1， 采用dart树，均匀不放回抽样，新生成的树的权重等于所有被抛弃的树的权重的均值，每一轮迭代时抛弃树的比例为20%，每一轮迭代时可以不执行dropout的概率为0.5
# 进行5折交叉验证下的100次迭代的数据

data_xgb = xgb.DMatrix(X,y)
params_dart = {"max_depth":5 ,"seed":1412, "eta":0.1
                  ,"booster":"dart","sample_type": "uniform"
                  ,"normalize_type":"tree"
                  ,"rate_drop": 0.2
                  ,"skip_drop": 0.5}
result_dart = xgb.cv(params_dart,data_xgb,num_boost_round=100
                ,nfold=5 #补充交叉验证中所需的参数，nfold=5表示5折交叉验证
                ,seed=1412 #交叉验证的随机数种子，params中的是管理boosting过程的随机数种子
               )

弱评估器的训练数据

  • 样本的抽样

    • 参数subsample：对样本进行抽样的比例，默认为1，可输入(0,1]之间的任何浮点数。例如，输入0.5，则表示随机抽样50%的样本进行建树。

    当该参数设置为1时，表示使用原始数据进行建模，不进行抽样。同时，XGBoost中的样本抽样是不放回抽样，因此不像GBDT或者随机森林那样存在袋外数据的问题，同时也无法抽样比原始数据更多的样本量。因此，抽样之后样本量只能维持不变或变少，如果样本量较少，建议保持subsample=1。

    • 参数sampling_method：对样本进行抽样时所使用的抽样方法，默认均匀抽样。

    输入"uniform"：表示使用均匀抽样，每个样本被抽到的概率一致。如果使用均匀抽样，建议subsample的比例最好在0.5或以上。


    需要注意的是，该参数还包含另一种可能的输入"gradient_based"：表示使用有权重的抽样，并且每个样本的权重等于该样本的gi2+λhi2\sqrt{g_i^2 +\lambda h_i^2}gi2​+λhi2​​。但该输入目前还不支持XGBoost当中主流的gbtree等建树方法，因此一般我们不会用到。

  • 特征的抽样

    • 参数colsample_bytree，colsample_bylevel，colsample_bynode，这几个参数共同控制对特征所进行的抽样。

      所有形似colsample_by*的参数都是抽样比例，可输入(0,1]之间的任何浮点数，默认值都为1。

      对于GBDT、随机森林来说，特征抽样是发生在每一次建树之前。但对XGBoost来说，特征的抽样可以发生在建树之前（由colsample_bytree控制）、生长出新的一层树之前（由colsample_bylevel控制）、或者每个节点分枝之前（由colsample_bynode控制）。

      三个参数之间会互相影响，全特征集 >= 建树所用的特征子集 >= 建立每一层所用的特征子集 >= 每个节点分枝时所使用的特征子集。

      举例说明：假设原本有64个特征，参数colsample_bytree等于0.5，则用于建树的特征就只有32个。此时，如果colsample_bylevel不为1，也为0.5，那新建层所用的特征只能由16个，并且这16个特征只能从当前树已经抽样出的32特征中选择。同样的，如果colsample_bynode也不为1，为0.5，那每次分枝之前所用的特征就只有8个，并且这8个特征只能从当前层已经抽样出的16个特征中选择。

      在实际使用时，我们可以让任意抽样参数的比例为1，可以在某一环节不进行抽样。一般如果特征量太少（例如，10个以下），不建议同时使用三个参数。

提前停止

  • 提前停止

参数early_stopping_rounds：位于xgb.train方法当中。如果规定的评估指标不能连续early_stopping_rounds次迭代提升，那就触发提前停止。

  • 模型监控与评估

参数evals：位于xgb.train方法当中，用于规定训练当中所使用的评估指标，一般都与损失函数保持一致，也可选择与损失函数不同的指标。该指标也用于提前停止。


参数verbosity：用于打印训练流程和训练结果的参数。在最早的版本中该参数为silent，后来经过更新变成了今天的verbosity。然而，经过改进之后的verbosity更倾向于帮助我们打印建树相关的信息，而不像原来的silent一样帮助我们展示训练过程中的模型评估信息，因此verbosity现在不那么实用了。

我们可以在verbosity中设置数字[0,1,2,3]，参数默认值为1。

  • 0：不打印任何内容
  • 1：表示如果有警告，请打印警告
  • 2：请打印建树的全部信息
  • 3：我正在debug，请帮我打印更多的信息。
  • 样本不均衡

参数scale_pos_weight：调节样本不均衡问题，类似于sklearn中的class_weight，仅在算法执行分类任务时有效。参数scale_pos_weight的值可以是负样本比正样本的比例，默认为1，因此XGBoost时默认调节样本均衡的。同时，如果你需要手动设置这个参数，通常可以设置为（负样本总量）/（正样本总量）这样的值。

  • 并行的线程

参数nthread：允许并行的最大线程数，类似于sklearn中的n_jobs，默认为最大，因此xgboost在默认运行时就会占用大量资源。如果数据量较大、模型体量较大，可以设置比最大线程略小的线程，为其他程序运行留出空间。

确定XGBoost优化的参数空间

XGBoost各参数对算法的影响：

影响力参数
⭐⭐⭐⭐⭐
几乎总是具有巨大影响力		num_boost_round（整体学习能力）
eta（整体学习速率）
⭐⭐⭐⭐
大部分时候具有影响力		booster（整体学习能力）
colsample_by*（随机性）
gamma（结构风险 + 精剪枝）
lambda（结构风险 + 间接剪枝）
min_child_weight（精剪枝）
⭐⭐
可能有大影响力
大部分时候影响力不明显		max_depth（粗剪枝）
alpha（结构风险 + 精剪枝）
subsamples（随机性）
objective（整体学习能力）
scale_pos_weight（样本不均衡）
⭐
当数据量足够大时，几乎无影响		seed
base_score（初始化）

特别注意：

  1. 在随机森林中影响力巨大的max_depth在XGBoost中默认值为6，比GBDT中的调参空间略大，但还是没有太多的空间，因此影响力不足。

  2. 在GBDT中影响力巨大的max_features对标XGBoost中的colsample_by*系列参数，原则上来说影响力应该非常大，但由于三个参数共同作用，调参难度较高，在只有1个参数作用时效果略逊于max_features。

  3. 精剪枝参数往往不会对模型有太大的影响，但在XGBoost当中，min_child_weight与结构分数的计算略微相关，因此有时候会展现出较大的影响力。故而将这个精剪枝参数设置为4星参数。

  4. 类似于objective这样影响整体学习能力的参数一般都有较大的影响力，但XGBoost当中每种任务可选的损失函数不多，因此一般损失函数不在调参范围之内，故认为该参数的影响力不明显。

  5. XGBoost的初始化分数只能是数字，因此当迭代次数足够多、数据量足够大时，起点的影响会越来越小。因此我们一般不会对base_score进行调参。

优先会考虑影响力巨大的参数（5星参数），当算力足够/优化算法运行较快的时候，我们可以考虑将大部分时候具有影响力的参数（4星）也都加入参数空间。一般来说，只要样本量足够，我们还是愿意尝试subsample以及max_depth，如果算力充足，我们还可以加入obejctive这样或许会有效的参数。

需要说明的是：

  • 一般不会同时使用三个colsample_by*参数、更不会同时调试三个colsample_by*参数。首先，参数colsample_bylevel较为不稳定，不容易把握，因此**当训练资源充足时，会同时调整colsample_bytree和colsample_bynode。**如果计算资源不足，或者优先考虑节约计算时间，则会先选择其中一个参数、尝试将特征量控制在一定范围内来建树，并观察模型的结果。在这三个参数中，使用bynode在分枝前随机，比使用bytree建树前随机更能带来多样性、更能对抗过拟合，但同时也可能严重地伤害模型的学习能力。
  • 对于有界且范围区间为1的参数（比如colsample_bynode，subsamples、eta等），或者有固定选项的参数（比如booster,objective），无需确认参数空间。
  • 对取值较小的参数（例如树模型的min_impurity_decrease等），或者通常会向下调整的参数（比如max_depth），一般是围绕默认值向两边展开构建参数空间。
  • 对于取值可大可小，且原则上可取到无穷值的参数（num_boost_round，gamma、lambda、min_child_weight等），一般需要绘制学习曲线进行提前探索，或者也可以设置广而稀的参数空间，来一步步缩小范围。
import xgboost as xgb
data_xgb = xgb.DMatrix(X,y)

#定义一个函数，用来检测模型迭代完毕后的过拟合情况
def overfitcheck(result):
    return (result.iloc[-1,2] - result.iloc[-1,0]).min()

num_boost_round参数范围搜索

# 可视化xgboost在参数空间为max_depth=5, 随机种子为1412， 学习率为0.1， 
# 进行5折交叉验证下进行300次以内的迭代的折线图（包括训练集，测试集和迭代完毕后的过拟合情况）

train = []
test = []
option = np.arange(10,300,10)
overfit = []
for i in option:
    params = {"max_depth":5,"seed":1412,"eta":0.1, "nthread":16
             }
    result = xgb.cv(params,data_xgb,num_boost_round=i
                ,nfold=5 #补充交叉验证中所需的参数，nfold=5表示5折交叉验证
                ,seed=1412 #交叉验证的随机数种子，params中的是管理boosting过程的随机数种子
               )
    overfit.append(overfitcheck(result))
    train.append(result.iloc[-1,0])
    test.append(result.iloc[-1,2])
plt.plot(option,test)
lot(option,train)
plt.plot(option,overfit)
# 缩小纵坐标范围
plt.ylim(20000,30000);

min_child_weight参数范围搜索

# 可视化xgboost在参数空间为max_depth=5, 随机种子为1412， 学习率为0.1，min_child_weight设置为【0，100】
# 进行5折交叉验证下进行50次以内的迭代的折线图（包括训练集，测试集和迭代完毕后的过拟合情况）（删去下面两格）（code）
train = []
test = []
option = np.arange(0,100,1)
overfit = []
for i in option:
    params = {"max_depth":5,"seed":1412,"eta":0.1, "nthread":16
              ,"min_child_weight":i
             }
    result = xgb.cv(params,data_xgb,num_boost_round=50
                ,nfold=5 #补充交叉验证中所需的参数，nfold=5表示5折交叉验证
                ,seed=1412 #交叉验证的随机数种子，params中的是管理boosting过程的随机数种子
               )
    overfit.append(overfitcheck(result))
    train.append(result.iloc[-1,0])
    test.append(result.iloc[-1,2])
plt.plot(option,test)
lot(option,train)
plt.plot(option,overfit)

全部参数的参数空间

参数范围
num_boost_round学习曲线探索，最后定为
(50,200,10)
eta以0.3为中心向两边延展，最后定为
(0.05,2.05,0.05)
booster两种选项
[“gbtree”,“dart”]
colsample_bytree设置为(0,1]之间的值，但由于还有参数bynode，因此整体不宜定得太小，因此定为
(0.3,1,0.1)
colsample_bynode设置为(0,1]之间的值，定为
(0.1,1,0.1)
gamma学习曲线探索，有较大可能需要改变，定为
(1e6,1e7,1e6)
lambda学习曲线探索，定为
(0,3,0.2)
min_child_weight学习曲线探索，定为
(0,50,2)
max_depth以6为中心向两边延展，右侧范围定得更大
(2,30,2)
subsample设置为(0,1]之间的值，定为
(0.1,1,0.1)
objective两种回归类模型的评估指标
[“reg:squarederror”, “reg:squaredlogerror”]
rate_drop如果选择"dart"树所需要补充的参数，设置为(0,1]之间的值
(0.1,1,0.1)

基于TPE对XGBoost进行优化

# 导入日常使用库与算法
import pandas as pd
import numpy as np
import sklearn
import matplotlib as mlp
import matplotlib.pyplot as plt
import time
import xgboost as xgb

# 导入优化算法相关的库
import hyperopt
from hyperopt import hp, fmin, tpe, Trials, partial
from hyperopt.early_stop import no_progress_loss

# 导入train_encode文件
data = pd.read_csv("train_encode.csv",index_col=0)

# 定义特征数据集和标签数据集
X = data.iloc[:,:-1]
y = data.iloc[:,-1]

  • 定义目标函数

    def hyperopt_objective(params):
    paramsforxgb = {"eta":params["eta"]
                    ,"booster":params["booster"]
                    ,"colsample_bytree":params["colsample_bytree"]
                    ,"colsample_bynode":params["colsample_bynode"]
                    ,"gamma":params["gamma"]
                    ,"lambda":params["lambda"]
                    ,"min_child_weight":params["min_child_weight"]
                    ,"max_depth":int(params["max_depth"])
                    ,"subsample":params["subsample"]
                    ,"objective":params["objective"]
                    ,"rate_drop":params["rate_drop"]
                    ,"nthread":14
                    ,"verbosity":0
                    ,"seed":1412}
    result = xgb.cv(params,data_xgb, seed=1412, metrics=("rmse")
                    ,num_boost_round=int(params["num_boost_round"]))
    return result.iloc[-1,2]

  • 定义参数空间

    param_grid_simple = {'num_boost_round': hp.quniform("num_boost_round",50,200,10)
                     ,"eta": hp.quniform("eta",0.05,2.05,0.05)
                     ,"booster":hp.choice("booster",["gbtree","dart"])
                     ,"colsample_bytree":hp.quniform("colsample_bytree",0.3,1,0.1)
                     ,"colsample_bynode":hp.quniform("colsample_bynode",0.1,1,0.1)
                     ,"gamma":hp.quniform("gamma",1e6,1e7,1e6)
                     ,"lambda":hp.quniform("lambda",0,3,0.2)
                     ,"min_child_weight":hp.quniform("min_child_weight",0,50,2)
                     ,"max_depth":hp.choice("max_depth",[*range(2,30,2)])
                     ,"subsample":hp.quniform("subsample",0.1,1,0.1)
                     ,"objective":hp.choice("objective",["reg:squarederror","reg:squaredlogerror"])
                     ,"rate_drop":hp.quniform("rate_drop",0.1,1,0.1)
                    }

  • 定义优化函数

    def param_hyperopt(max_evals=100):
    
    #保存迭代过程
    trials = Trials()
    
    #设置提前停止
    early_stop_fn = no_progress_loss(30)
    
    #定义代理模型
    params_best = fmin(hyperopt_objective
                       , space = param_grid_simple
                       , algo = tpe.suggest
                       , max_evals = max_evals
                       , verbose=True
                       , trials = trials
                       , early_stop_fn = early_stop_fn
                      )
    
    #打印最优参数，fmin会自动打印最佳分数
    print("\n","\n","best params: ", params_best,
          "\n")
    return params_best, trials

  • 训练5次贝叶斯优化器

    params_best, trials = param_hyperopt(100)
params_best, trials = param_hyperopt(100)
params_best, trials = param_hyperopt(100)
params_best, trials = param_hyperopt(100)
params_best, trials = param_hyperopt(100)

    根据5次贝叶斯优化器的结果调整参数空间

12345
num_boost_round200110170110180
booster11011
objective00000
colsample_bynode0.80.51.00.30.9
colsample_bytree0.81.00.51.00.4
eta1.550.50.051.01.3
gamma2e61e77e67e69e6
lambda0.21.62.401.2
max_depth22988
min_child_weight00024
rate_drop0.20.70.70.40.1
subsample0.90.70.60.71

首先，objective在所有迭代中都被选为"reg:squarederror"，这也是xgboost的默认值，因此不再对该参数进行搜索。同样的。booster参数在5次运行中有4次被选为"dart"，因此基本可以确认对目前的数据使用DART树是更好的选择。同时在参考结果时我们就可以不太考虑第三次搜索的结果，因为第三次搜索是给予普通gbtree给出的结果。

对于其他参数，我们则根据搜索结果修改空间范围、增加空间密度，一般让范围向选中更多的一边倾斜，并且减小步长。例如num_boost_round从来没有选到100以下的值，还有一次触顶，两次接近上限，因此可以将原本的范围(50,200,10)修改为(100,300,10)。colsample_bynode的结果均匀地分布在0.3~1之间，可以考虑不更换范围，但缩小步长。colsample_bytree的结果更多偏向于1.0，因此可以考虑提升下限。

  • 调整参数空间

    param_grid_simple = {'num_boost_round': hp.quniform("num_boost_round",100,300,10)
                     ,"eta": hp.quniform("eta",0.05,2.05,0.05)
                     ,"colsample_bytree":hp.quniform("colsample_bytree",0.5,1,0.05)
                     ,"colsample_bynode":hp.quniform("colsample_bynode",0.3,1,0.05)
                     ,"gamma":hp.quniform("gamma",5e6,1.5e7,5e5)
                     ,"lambda":hp.quniform("lambda",0,2,0.1)
                     ,"min_child_weight":hp.quniform("min_child_weight",0,10,0.5)
                     ,"max_depth":hp.choice("max_depth",[*range(2,15,1)])
                     ,"subsample":hp.quniform("subsample",0.5,1,0.05)
                     ,"rate_drop":hp.quniform("rate_drop",0.1,1,0.05)
                    }

  • 调整目标函数

    def hyperopt_objective(params):
    paramsforxgb = {"eta":params["eta"]
                    ,"colsample_bytree":params["colsample_bytree"]
                    ,"colsample_bynode":params["colsample_bynode"]
                    ,"gamma":params["gamma"]
                    ,"lambda":params["lambda"]
                    ,"min_child_weight":params["min_child_weight"]
                    ,"max_depth":int(params["max_depth"])
                    ,"subsample":params["subsample"]
                    ,"rate_drop":params["rate_drop"]
                    ,"booster":"dart"
                    ,"nthred":14
                    ,"verbosity":0
                    ,"seed":1412}
    result = xgb.cv(params,data_xgb, seed=1412, metrics=("rmse")
                    ,num_boost_round=int(params["num_boost_round"]))
    return result.iloc[-1,2]

  • 训练5次贝叶斯优化器

    params_best, trials = param_hyperopt(100)
params_best, trials = param_hyperopt(100)
params_best, trials = param_hyperopt(100)
params_best, trials = param_hyperopt(100)
params_best, trials = param_hyperopt(100)

  • 选取损失值最小的一组参数进行验证

    def hyperopt_validation(params):
    paramsforxgb = {"eta":params["eta"]
                    ,"booster":"dart"
                    ,"colsample_bytree":params["colsample_bytree"]
                    ,"colsample_bynode":params["colsample_bynode"]
                    ,"gamma":params["gamma"]
                    ,"lambda":params["lambda"]
                    ,"min_child_weight":params["min_child_weight"]
                    ,"max_depth":int(params["max_depth"])
                    ,"subsample":params["subsample"]
                    ,"rate_drop":params["rate_drop"]
                    ,"nthred":14
                    ,"verbosity":0
                    ,"seed":1412}
    result = xgb.cv(params,data_xgb, seed=1412, metrics=("rmse")
                    ,num_boost_round=int(params["num_boost_round"]))
    return result.iloc[-1,2]

    bestparams = {'colsample_bynode': 0.45
               , 'colsample_bytree': 1.0
               , 'eta': 0.05
               , 'gamma': 13000000.0
               , 'lambda': 0.5
               , 'max_depth': 6
               , 'min_child_weight': 0.5
               , 'num_boost_round': 150.0
               , 'rate_drop': 0.65
               , 'subsample': 0.8500000000000001} 

    # 对训练完得到的最优参数进行验证，打印运行时间
start = time.time()
hyperopt_validation(bestparams)
end = (time.time() - start)
print(end)

参考资料

  1. 菜菜机器学习实战课程
  2. https://blog.csdn.net/Yongchun_Zhu/article/details/78745529
xgboost 算法原理
哆啦A梦的博客
10-18 7万+
1、xgboost是什么全称：eXtreme Gradient Boosting 作者：陈天奇(华盛顿大学博士) 基础：GBDT 所属：boosting迭代型、树类算法。 适用范围：分类、回归 优点：速度快、效果好、能处理大规模数据、支持多种语言、支 持自定义损失函数等等。 缺点：发布时间短（2014），工业领域应用较少，待检验2、基础知识，GBDTxgboost
(九)XGBoost的原理、具体实例、代码实现
user_28608的博客
10-10 9750
XGBoost，全称eXtreme Gradient Boosting ，简称XGB，是GBDT算法的一种变种，是一种监督算法；它是boost算法的一种，也属于集成算法，是一种伸缩性强、便捷的可并行构建模型的Gradient Boosting算法。其高效地实现了GBDT算法并进行了算法和工程上的许多改进，被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中。并取得了不错的成绩。它可用于分类，回归，排序问题。
Python代码实现XGBoost算法，超详细版
liuqi17866512431的博客
10-14 675
本文介绍了一个基于Python的XGBoost分类算法实现流程。主要内容包括：1）使用pandas加载数据并进行标签编码；2）通过train_test_split划分训练集和测试集；3）构建XGBClassifier模型并训练；4）利用测试集评估模型性能，输出混淆矩阵和分类报告；5）可视化混淆矩阵并保存结果。文章详细说明了XGBoost参数调优方法，如n_estimators、learning_rate等参数的意义和设置建议，并提供了多分类任务的处理方式。该实现虽然简化但结构清晰，可作为XGBoost算法应
XGBoost与Lightgbm
chenguiyuan1234的博客
02-25 621
本文参考自https://cloud.tencent.com/developer/article/1389899 https://cloud.tencent.com/developer/article/1052678 https://cloud.tencent.com/developer/article/1052664 XGBoost 1、重要参数详解 booster[default=gbtree...
xgboost代码
06-15
关于xgboost的代码，可以跑起来。实现了分类关于xgboost的代码，可以跑起来。实现了分类
xgboost源代码
05-08
本人通过亲自实践，教大家一步步在win下安装xgboost(http://blog.csdn.net/jingyi130705008/article/details/71435562)，这个是之前的xgboost的C++版本，是在python使用xgboost之前必须的包。
xgboost-whl安装包（包含32位和64位）
09-07
**WHL文件** 是Python的Wheel格式安装包，它是Python的二进制分发格式，用于简化安装过程，避免编译源代码。WHL文件通常与Python的版本和系统架构相对应，例如，对于32位Python 3.7，会有对应的`xgboost-版本号-cp37...
xgboost-0.80-cp36-cp36m-win_amd64.whl下载.zip
03-21
4. **验证安装**：安装完成后，可以运行一段简单的代码来验证XGBoost是否已经成功安装。例如： ```python import xgboost as xgb print(xgb.__version__) ``` 如果没有报错并打印出0.80，那么恭喜你，XGBoost...
编译过的xgboost-master
03-24
3. **验证安装**：通过运行简单的示例代码，验证xgBoost是否正确安装并可用。 4. **开始使用**：在项目中导入xgBoost库，构建模型并进行训练。 总之，“编译过的xgBoost-master”是一个便捷的机器学习工具，为数据...
arima的matlab代码-Time-Series-ARIMA-XGBoost-RNN:时间序列预测：ARI
最新发布
10-22
在Python代码实现方面，提供了两个可执行文件：Gpower_Arima_Main.py 和 Gpower_Xgb_Main.py，分别对应单变量ARIMA模型和基于树的XGBoost模型。此外，还提供了myArima.py和myXgb.py这两个辅助函数库，用于实现相应的...
机器学习中Xgboost-Shap模型解释与特征重要性可视化的应用
04-06
文中提供了具体的Python代码实例，分别针对回归任务（如波士顿房价预测）和分类任务（如鸢尾花数据集分类），展示了如何使用Xgboost进行建模以及如何利用Shap进行特征重要性的可视化分析。此外，还讨论了一些常见的...
XGBoost代码附带示例和数据
06-14
该代码使用XGBoost进行分类预测，在python环境下进行操作，附带多个数据示例展示集相应的数据集，并进行不同算法对比
xgboost源代码python
11-27
根据我的课程设计写了一个xgboost代码，效果不错。希望能帮助跟我一样的初学者。
XGBoost算法使用代码示例
10-06
XGBoost算法使用代码示例讲解，由原作者创作，语言使用R语言
利用python中的xgboost对超市销量进行预测
11-19
资源包括某超市四个月的各大中小类的销售记录，代码利用星期特征，去除噪声，用xgboost进行预测，代码中包含了一些基础的分析方法，可供新手参考。
xgboost的代码
weixin_42577243的博客
01-17 904
XGBoost是一个用于在线学习和离线梯度提升的工具。它通常用于分类和回归问题。 在Python中使用XGBoost的代码示例如下： import xgboost as xgb# 创建训练数据 dtrain = xgb.DMatrix(X_train, label=y_train) # 设置参数 params = {'max_depth': 2, 'eta': 0.1} # 训练模型 mode...
树模型(六)：XGBoost
热门推荐
雪伦的专栏
04-21 19万+
文章内容可能会相对比较多，读者可以点击上方目录，直接阅读自己感兴趣的章节。1.序　　距离上一次编辑将近10个月，幸得爱可可老师（微博）推荐，访问量陡增。最近毕业论文与xgboost相关，于是重新写一下这篇文章。　　关于xgboost的原理网络上的资源很少，大多数还停留在应用层面，本文通过学习陈天奇博士的PPT、论文、一些网络资源，希望对xgboost原理进行深入理解。（笔者在最后的参考文献中会给出地
机器学习之XGboost代码实现
蜗牛遥遥
03-18 1万+
XGboost代码实现 XGboost的原生语言是c++，所以它的运行速度比较快。这里将会举例介绍一下python中如何调用XGboost，如果想了解XGboost的理论部分，可以参考这篇博客 首先要安装XGboost库 pip install XGboost 数据集：以鸢尾花数据集为例 例1 # /usr/bin/python # -*- encoding:utf-8 -*- from sk...
XGBoost算法Python代码实现
彬彬侠的博客
11-09 2498
这段代码实现了一个基础的 XGBoost 算法，涵盖了梯度提升的核心逻辑和分类预测流程。尽管与正式的 XGBoost 实现相比有所简化，但它提供了一个清晰的框架，适合用于理解 XGBoost 的原理和实现方式。在实际应用中，可以根据需求扩展功能，提升模型性能和效率。
XGBoost-CPO代码讲解
02-23
### XGBoost与CPO结合使用的代码讲解 #### 使用mlr3框架中的CPO操作符优化XGBoost模型 为了实现更灵活的数据预处理流程，在`mlr3pipelines`包中引入了复合管道操作(CPO)，这使得可以轻松地将数据转换逻辑集成到...
评论 1
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值