深入剖析移动最小二乘，实现曲线拟合 python实现

移动最小二乘

顾名思义就是移动着求最小二乘，把区间分段的求最小二乘，分段越小自然效果越好，分段越大，自然效果越差，就是利用微分的思想。

数学推导

相比于最小二乘，移动最小二乘建立的拟合函数是采用分段拟合以及平滑化。由一个系数向量和一个基函数p(x)构成。
我们可以先把一个区间分成若干个局部子区间，每个子区间进行最小二乘的拟合，子区间的函数可以表示为：




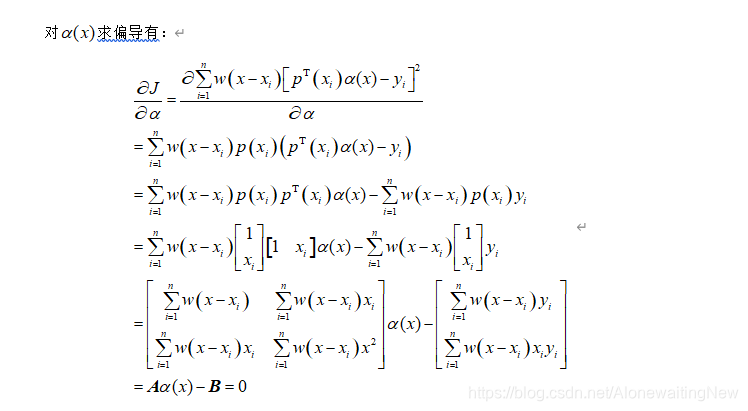
权函数应该是非负的，并且和距离成反比。权函数还应该具有一定的光滑性，因为拟合函数会继承权函数的连续性。如果权函数n阶连续，对应的拟合函数也是n阶连续的。记

总结

移动最小二乘中，最关键的部分就是权重函数，在一定的区域内权重是有效值，在超出这个区域内为0，也就是说该方法在逐步的分段的求解这个拟合函数，就是任意一个二维的曲线，我们可以认为是由多个折现组成，这也是微分的一种思想。

代码实现

（这里是直接参考别人的函数的）
生成的随机点，然后加上一定的误差。
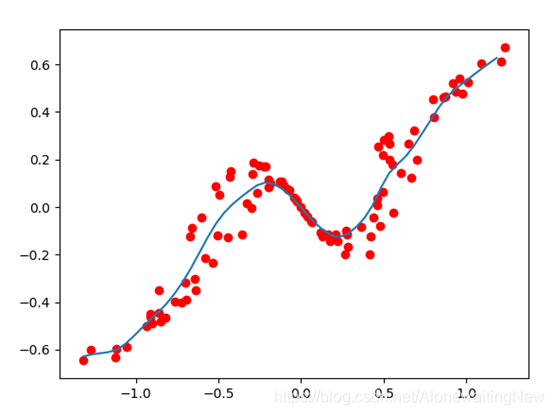
蓝色的线为拟合后的效果，蓝色的线将区间[-1,1]分成了40分，为此我们得到40份的分段函数，由于40段太长。重新调整移动的步长为0.5，这样一来只有6个区间。我们把拟合的函数绘制出来，并且把分段函数打印出来有：


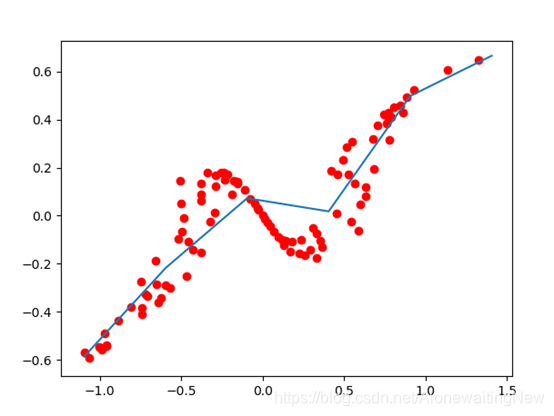
至此已完全实现移动最小二乘的曲线拟合，可以看到效果还是蛮好的，当然了，对于步长越短效果会更好，但是对应的运行时间更长了，对应步长越长效果自然较差。对于该方法如果需要改进只能从权函数入手。

python代码

# -*- coding: utf-8 -*-

'''
@Time    : 2019/12/16 17:38
@Author  : DWY
@FileName: MLS.py
@Software: PyCharm Community Edition
 
'''
import numpy as np
import matplotlib.pyplot as plt
step=0.05
#权函数
def w(dis):
    dis = dis / 0.3
    if dis < 0:
        return 0
    elif dis <= 0.5:
        return 2/3 - 4 * dis**2 + 4 * dis**3
    elif dis <= 1:
        return 4/3 - 4 * dis + 4 * dis**2 - 4/3 * dis**3
    else:
        return 0


def mls(x_):
    sumxx = sumx = sumxf = sumf = sumw = 0
    for (a, b) in zip(x, y):
        weight = w(abs(x_ - a))
        sumw += weight
        sumx += a * weight
        sumxx += a * a * weight
        sumf += b * weight
        sumxf += a * b * weight
    A = np.array([[sumw, sumx],
                  [sumx, sumxx]])#A
    B = np.array([sumf, sumxf])#B
    ans = np.linalg.solve(A, B)
    print("%f+%f*x,{x|%f<x<%f}"%(ans[0],ans[1],x_,x_+step))
    return ans[0] + ans[1] * x_

#主题部分
import random
#生成曲线上的各个点
x = np.arange(-1,1,0.02)
y = [((a*a-1)*(a*a-1)*(a*a-1)+0.5)*np.sin(a*2) for a in x]

# 生成的曲线上的各个点偏移一下，并放入到xa,ya中去
i = 0
xa = []
ya = []
for xx in x:
    yy = y[i]
    d = float(random.randint(60, 140)) / 100
    # ax.plot([xx*d],[yy*d],color='m',linestyle='',marker='.')
    i += 1
    xa.append(xx * d)
    ya.append(yy * d)
x = xa
y = ya
miny = min(xa)
maxy = max(xa)
xx = np.arange(miny, maxy+step, step)
yy = [mls(xi) for xi in xx]
plt.plot(xx, yy)
plt.scatter(x, y, c='r')
plt.show()
#其他函数部分
#权函数

以上代码直接能运行