一、梯度下降算法
以函数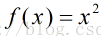
(1)求梯度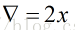
(2)向梯度相反方向移动x, 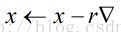
(3)循环迭代步骤(2),直到x的变化到使得f(x)在两次迭代之间的差值足够小,比如0.00000001,即直到两次迭代计算出来的f(x)基本没有变化,则说明此时f(x)已经达到局部最小值了;
(4)输出x,这个x就是使函数f(x)最小时x的取值
注意:梯度的方向就是导数最大值的方向,即函数变化率最快的方向。因此,梯度方向可以通过对函数求导得到。
梯度下降算法计算过程
(1)初始化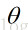
(2)迭代,新的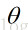
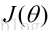
(3)如果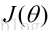
例如,线性回归目标函数的梯度方向计算
梯度下降








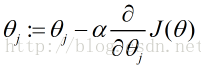
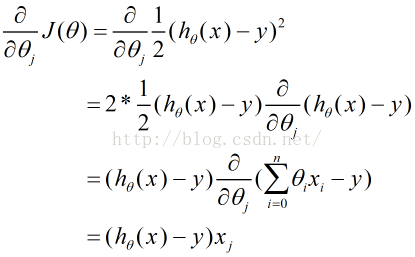
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 2341
2341











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








