数据结构基础知识核心归纳(一)
转载请声明出处:http://blog.csdn.net/andrexpert/article/details/77900395
Android Java 数据结构
Android基础技术核心归纳(一) Java基础技术核心归纳(一) 数据结构基础知识核心归纳(一)
Android基础技术核心归纳(二) Java基础技术核心归纳(二) 数据结构基础知识核心归纳(二)
Android基础技术核心归纳(三) Java基础技术核心归纳(三) 数据结构基础知识核心归纳(三)
Android基础技术核心归纳(四) Java基础技术核心归纳(四)
不知不觉又是一年的9月,今天跟一个师弟聊天,谈到了他现在面试的一些情况,突然想起自己当年也是这么走过来的,顿时感慨良多。Android/Java经验汇总系列文章,是当初自己毕业时笔试、面试和项目开发中相关的总结,虽然不是很高深的东西,也没有归纳得很全面,但是对Android、算法、Java把握个大概还是没问题,今天特意将这些文章放出来,希望能够对看到这个系列文章的毕业生朋友一点帮助吧。当然,由于受当时知识面的限制,归纳得可能不是很准确,若有疑问就留言哈。
1.浅谈栈、队列、堆的区别?
1.堆:堆是一种树状的数据结构。一般由程序员分配释放,存放由new创建的对象和数组(C中是由malloc分配和free释放),JVM不定时查看这个对象,如果没有引用指向这个对象就回收.
(1)优点:可动态分配内存大小,生成周期不必事先告诉编译器,Java垃圾回收自动回收数据;
(2)缺点:运行时需动态分配内存,因此,数据存储速度较慢
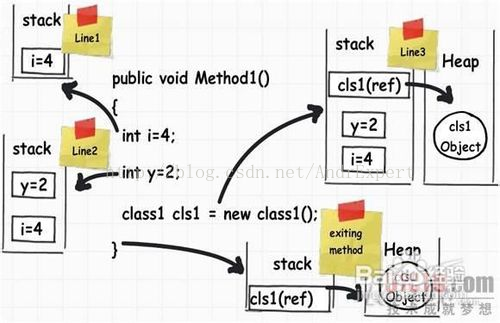
2.栈:是一种仅允许在一端进行插入和删除的线性表,即先进后出。由编译器自动分配释放,存放函数的参数值、局部变量的值等基本类型的变量和对象的引用。
(1)优点:存储速度比较块,仅次于寄存器且栈数据可以共享;
(2)缺点:存在栈中的数据大小与生存期必须是确定的(int y=4,y在栈中占4字节),缺乏灵活性
3.队列:是一种仅允许在尾端进行插入数据元素,首端进行删除数据元素的线性表,即先进先出FIFO。在队列中,数据元素可以任意增减,但数据元素的次序不会改变。每当有数据元素从队列中被取出,后面的数据元素一次向前移动一位。
参考:http://www.sxt.cn/u/1349/blog/2330
2.浅谈数组与链表的区别?
(1)从逻辑结构来看:数组必须实现定义固定的长度(元素个数),不能适应数据动态地增减的情况。当数据增加时,可能会造成溢出;当数据减少时,造成内存浪费,数组中插入、删除数据项时,需要移动其他数据项。链表动态地进行存储分配,可以使用数据动态地增减情况,可以节约内存,且可以方便地插入、删除数据数据项。
(2)从内存存储来看:(静态)数组从栈中分配空间(注:用new创建的在堆中分配),存储速度快但缺乏灵活性;链表从堆中分配空间,灵活性好但是申请管理比较麻烦;
(3)从访问方式来看:数组在内存中是连续存储的,因此可利用下标索引进行随机访问;链表是链式存储结构,在访问元素的时候只能通过线性的方法由前到后顺序访问,所以访问效率比数组要低。
3.单链表的创建、插入和删除操作?
1.单链表创建、插入、删除
(1)结点结构体
/***struct Node *即存储的是类型数据地址
而后继结点即为struct Node类** */
typedef struct
{
int data; //结点数据域 ,存放数据
struct Node *next; //结点指针域,指针变量next存放struct Node *类型变量存储地址(指向结点)
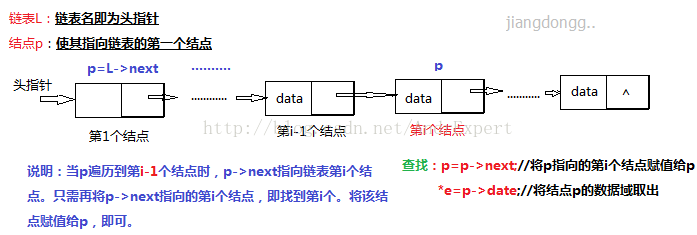
}Node,*LinkList; //Node表示结点,*LinkList 定义一个链表实现思想:首先,定义一个存储类型为结点地址的指针变量p,将第一个结点地址赋值给工作指针p。然后,初始化变量j并使其从1开始累加,当j<i时就遍历链表,工作指针p向后移动不断指向下一个结点,直到指向第i结点。若p指向null或者j大于要查询的位置时,查询失败;最后,取出第i个结点数据域中的数据,存放到指针变量e指向的存储空间。
/*功能:从单链表中读取第i个元素,1<=i<=ListLenght(L)
存放到指针e指向的存储地址中*/
#define UNSUCCESS -1
#define SUCCESS 1
typedef Status int;
Status GetElem(LinkList L,int i,int *e)
{
int j=1;
LinkList p; //声明一个结点p
p=L->next; //让结点p指向链表L的第一个结点
while(p&&j<i) { //从链表第一个结点开始遍历,直到j=i-1,让p指向存储i-1位置所在的结点
p=p->next; //让p指向下一个结点,
++j;
}
if(!p || j>i) //当p指向null或者j大于要查询的位置时,查询失败
return UNSUCCESS ;
*e=p->data; //查找成功,将链表中的第i个元素的数据存储到指针e指向的空间
return SUCCESS;
}实现思路:首先,对链表进行查询操作,找到第i个位置;其次,为新插入的结点s在内存中开辟一段存储空间并将插入的元素存储到新结点s的数据域中;最后,将p指向的结点位置赋值给新结点s的指针域,再将新结点s的存储地址赋值给工作指针。








 本文是数据结构基础知识的核心归纳,重点讨论了栈、队列和堆的区别,包括它们的内存分配、优缺点。同时,提到了数组与链表的差异,并简单介绍了单链表的创建、插入和删除操作。
本文是数据结构基础知识的核心归纳,重点讨论了栈、队列和堆的区别,包括它们的内存分配、优缺点。同时,提到了数组与链表的差异,并简单介绍了单链表的创建、插入和删除操作。

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 656
656

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








