【实验一】扰动更新_旋转的小扰动,旋转轴是可加的-CSDN博客

该博客主要探讨了在计算机图形学中如何使用罗德里格向量旋转公式和四元数进行旋转矩阵的更新。具体地，作者给出了给定旋转轴和角度的旋转矩阵，然后通过一个旋转更新小量，使用罗德里格公式计算了更新后的旋转矩阵，并与四元数更新的结果进行了误差比较。在代码实现部分，使用了Eigen库并展示了C++代码示例，最后输出了更新过程的误差矩阵。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

针对扰动小量更新的实现

在这里插入图片描述

在计算机图形学中，罗德里格向量旋转公式通常被用来填写旋转矩阵。如果把k和v分别写为列向量：
在这里插入图片描述
则旋转以后的向量可以表示为：

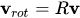
其中

其中E是3阶单位矩阵。需要注意的是，公式中的第二项不是点积，而是张量积，得到的是一个3行3列的矩阵。

代码如下：代码路径/home/wpf/SLAM/vio/vio_works/ch1/main.cpp

#include <iostream>
#include <eigen3/Eigen/Geometry>
#include <eigen3/Eigen/Core>
using namespace std;

int main() {
    //给定旋转轴和角度对应的旋转矩阵
    //给定旋转更新小量
    //使用罗德里戈公式进行更新
    //使用四元数进行更新
    //对比二者的误差
    Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI_4, Eigen::Vector3d(0, 0, 1)).toRotationMatrix();
    Eigen::Quaterniond q(R);

    Eigen::Vector3d w(0.01, 0.02, 0.03);

    cout << "给定的原始转换的旋转矩阵和无穷小量的旋转的扰动" << endl;
    cout << R << endl;
    //注意输出四元数的基本格式
    cout << q.coeffs().transpose() << endl;

    //更新方式一，使用罗德里戈公式进行更新。
    //旋转小量对应的小扰动为，求对应的轴和角度
    //返回是二范数，弧度制
    double theta = w.norm();
    //归一化更新旋转轴
    Eigen::Vector3d n_w = w / theta;
    Eigen::Matrix3d n_w_skew;
    n_w_skew << 0, -n_w(2), n_w(1),
            n_w(2), 0, -n_w(0),
            -n_w(1), n_w(0), 0;

    Eigen::Matrix3d R_W =
            Eigen::Matrix3d::Identity() * cos(theta) + (1 - cos(theta)) * n_w * n_w.transpose() + sin(theta) * n_w_skew;
    Eigen::Matrix3d R_update = R * R_W;
    //实部设为1??目前也只能设为1
    Eigen::Quaterniond q_w(1, 0.5 * w(0), 0.5 * w(1), 0.5 * w(2));
    //务必进行旋转归一化的操作，原因是仅有单位四元数表示一个旋转
    Eigen::Quaterniond q_update = (q * q_w).normalized();

    Eigen::Matrix3d diff = q_update.toRotationMatrix() - R_update;
    cout << diff << endl;

    std::cout << "Hello,wpf！" << std::endl;
    return 0;
}

对应的CMakeLists的文件

cmake_minimum_required(VERSION 3.20)
project(ch1)
include_directories("usr/include/eigen3")
set(CMAKE_CXX_STANDARD 14)
add_executable(ch1 main.cpp)

结果输出如下：

/home/wpf/SLAM/vio/vio_works/ch1/cmake-build-debug/ch1
给定的原始转换的旋转矩阵和无穷小量的
0.707107 -0.707107 0
0.707107 0.707107 0
0 0 1
0 0 0.382683 0.92388
2.5963e-06 2.37368e-06 -2.44789e-06
-2.38192e-06 2.53859e-06 -8.98416e-07
2.29623e-06 -1.23557e-06 5.83041e-08 Hello,wpf！

Process finished with exit code 0