本文内容基于《算法笔记》和官方配套练题网站“晴问算法”,是我作为小白的学习记录,如有错误还请体谅,可以留下您的宝贵意见,不胜感激。
前言
现实中的树是由树根、茎干、树枝、树叶组成的,树的营养是由树根出发、通过茎干与树枝来不断传递,最终到达树叶的。在数据结构中,树则是用来概括这种传递关系的一种数据结构。为了简化,数据结构中把树枝分叉处、树叶、树根抽象为结点(node),其中树根抽象为根结点(root),且对一棵树来说最多存在一个根结点:把树叶概括为叶子结点(leaf),且叶子结点不再延伸出新的结点;把茎干和树枝统一抽象为边(edge),且一条边只用来连接两个结点(一个端点一个)。这样,树就被定义为由若干个结点和若干条边组成的数据结构,且在树中的结点不能被边连接成环。在数据结构中,一般把根结点置于最上方(与现实中的树恰好相反),然后向下延伸出若干条边到达子结点(child)(从而向下形成子树(subtree)),而子结点又向下延伸出边并连接一些结点···直至到达叶子结点,看起来就像是把现实中的树颠倒过来的样子。(摘自算法笔记)
树是非线性逻辑结构的数据结构,是一对多的逻辑结构,可以通过静态二叉链表(数组)和二叉链表来实现。
一、树的性质
1.树可以没有结点,这种情况下把树称为空树(empty tree)。
2.树的层次(layer)从根结点开始算起,即根结点为第一层,根结点子树的根结点为第二层,以此类推。这里的层次可以用BFS来理解。
3.把结点的子树棵数称为结点的度(degree),而树中结点的最大的度称为树的度(也称为树的宽度)。
4.由于一条边连接两个结点,且树中不存在环,因此对有n个结点的树,边数一定是-1。(一个叶子结点有一条通向父节点的边,根节点没有)且满足连通、边数等于顶点数减1的结构一定是一棵树。
5.叶子结点被定义为度为0的结点,因此当树中只有一个结点(即只有根结点)时,根结点也算作叶子结点。
6.结点的深度(depth)是指从根结点(深度为1)开始自顶向下逐层累加至该结点时的深度值:结点的高度(height)是指从最底层叶子结点(高度为1)开始自底向上逐层累加至该结点时的高度值。树的深度是指树中结点的最大深度,树的高度是指树中结点的最天高度。对树而言,深度和高度是相等的,但是具体到某个结点来说深度和高度就不一定相等了。
7.多棵树组合在一起称为森林(forest),即森林是若干棵树的集合。
二、二叉树的递归定义
二叉树是具有递归性质的数据结构,每个节点都可以被看做根节点,即每个结点都是结构相同但规模不同,每个节点又都存在左子树和右子树,即使为空;二叉树的递归定义就是用自身来定义自身,二叉树的递归定义如下:
1.要么二叉树没有根节点,是一棵空树;
2.要么二叉树由根节点、左子树、右子树构成,且左子树和右子树都是二叉树。
区分二叉树和度为2的数:二叉树必须存在左子树和右子树,即使为空,并且二叉树的子树区分左右。
三、二叉树的存储结构
1.链表:
struct Node{
int data;
Node* lchild;
Node* rchild;
};
2.静态链表:
struct Node{
int lchild;
int rchild;
}node[MAXN];
四、二叉树的操作
1.链表新建结点:
Node* newnode(int data){
Node* node = new node;
node -> data = data;
node -> lchild = NULL;
node -> rchild = NULL;
return node;
}
2.遍历(搜索)
非线性逻辑结构的数据结构可以采用DFS和BFS的方式进行搜索,前面学习的时候知道这两种方法本质就是暴力枚举,核心是岔路口和死胡同的判断,岔路口就是左子树和右子树,死胡同就是空树。其中二叉树在DFS中又有三种搜索方法:先序、中序和后序,这三种方式的不同点就是在岔路口的顺序选择上不同:
先序总是先输出根节点,然后向左走,最后向右走;
中序总是先向左走,然后输出根节点,最后向右走;
后序总是先向左走,然后向右走,最后输出根节点;
以一个实例穿插4中搜索方式:

这个例子是让采用先序输出,保证其他题干不变的情况下,给出4种搜索方式,完整代码如下:
DFS:
#include<cstdio> //静态二叉链表
const int MAXN = 51;
struct Node{
int lchild;
int rchild;
}node[MAXN];
int count = 1 , n;
void rld(int root){ //先序遍历
if(root == -1) return;
printf("%d", root);
if(count < n) {
printf(" ");
count++;
}
rld(node[root].lchild);
rld(node[root].rchild);
}
void lrd(int root){ //中序遍历
if(root == -1) return;
lrd(node[root].lchild);
printf("%d", root);
if(count < n) {
printf(" ");
count++;
}
lrd(node[root].rchild);
}
void ldr(int root){ //后序遍历
if(root == -1) return;
ldr(node[root].lchild);
ldr(node[root].rchild);
printf("%d", root);
if(count < n) {
printf(" ");
count++;
}
}
int main(){
scanf("%d", &n);
for(int i = 0; i <= n - 1; i++)
scanf("%d%d", &node[i].lchild , &node[i].rchild);
ldr(0);
rld(0);
lrd(0);
}
BFS:
#include<cstdio>
#include<queue>
using namespace std;
const int MAXN = 51;
struct Node{
int lchild;
int rchild;
}node[MAXN];
int count = 1 , n;
void BFS(int root){
queue <int> qe;
qe.push(root);
while(!qe.empty()){
int top = qe.front();
qe.pop();
printf("%d", top);
if(count < n) {
printf(" ");
count++;
}
if(node[top].lchild != -1) qe.push(node[top].lchild);
if(node[top].rchild != -1) qe.push(node[top].rchild);
}
}
int main(){
scanf("%d", &n);
for(int i = 0; i <= n - 1; i++)
scanf("%d%d", &(*(node + i)).lchild , &(*(node + i)).rchild);
BFS(0);
}
若采用指针法链表,在队列中存放的元素最好是结点的地址,这样方便修改数据。
3.插入:
由于二叉树的形态很多,因此在题目不说明二叉树特点时是很难给出结点插人的具体方法的。但是又必须认识到,结点的插入位置一般取决于数据域需要在二叉树中存放的位置(这与二叉树本身的性质有关),且对给定的结点来说,它在二叉树中的插入位置只会有一个(如果结点有好几个插入位置,那么题目本身就有不确定性了)。因此可以得到这样一个结论,即二叉树结点的插入位置就是数据域在二叉树中查找失败的位置。而由于这个位置是确定的,因此在递归查找的过程中一定是只根据二叉树的性质来选择左子树或右子树中的一棵子树进行递归,且最后到达空树(死胡同)的地方就是查找失败的地方,也就是结点需要插入的地方。由此可以得到二叉树结点插入的代码:
void insert(node* &root , int x){
if(root == NULL){
root = newnode(x);
return;
}
if(由于二叉树的性质,x应该插在左子树) insert(root -> lchild , x);
else insert(root -> rchild , x);
}
4.创建二叉树:
创建二叉树就是将结点的数据域插入二叉树的过程;完整代码如下:
Node* create(int data[] , int n){
Node* root = NULL;
for(int i = 0; i <= n - 1; i++) insert(root , data[i]);
return root;
}
5.完全二叉树的存储结构:
由于完全二叉树的性质,任何一个结点(设编号为x),其左孩子的编号为2x,右孩子的编号为2x + 1,由于其结点地址的规律性,所以可以采用数组(静态链表)实现。普通二叉树也可以采用完全二叉树的存储方式,只是由于中间可能存在大量空结点, 会浪费很多空间。完全二叉树在数组中的存放顺序就是他的层次遍历顺序。
叶节点的标志:结点的左子结点下标x * 2 > n成立(右节点(x + 1) * 2 > n 肯定成立,所以不需要判断右子结点);
空节点的标志:结点的下标x > n成立;
五、先序、后序+中序遍历序列还原二叉树
先序、后序遍历序列可以提供树的根节点,而中序遍历序列可以根据根节点的位置找到树的左子树和右子树结点数量,根据这个数量可以对先序序列进行分区,将先序序列分为左子树和右子树,然后在左子树和右子树区间内继续上面的操作。所以可以采用分治法来解决这个问题:
分解子问题:首先根据先序、后序遍历序列确定树的根节点,在中序序列中找到这个根节点,计算左右子树的节点数量,对先序序列和中序序列进行分区,递归向左右子树确定新的根节点,和快速排序很相似。
通过实例来进行理解:
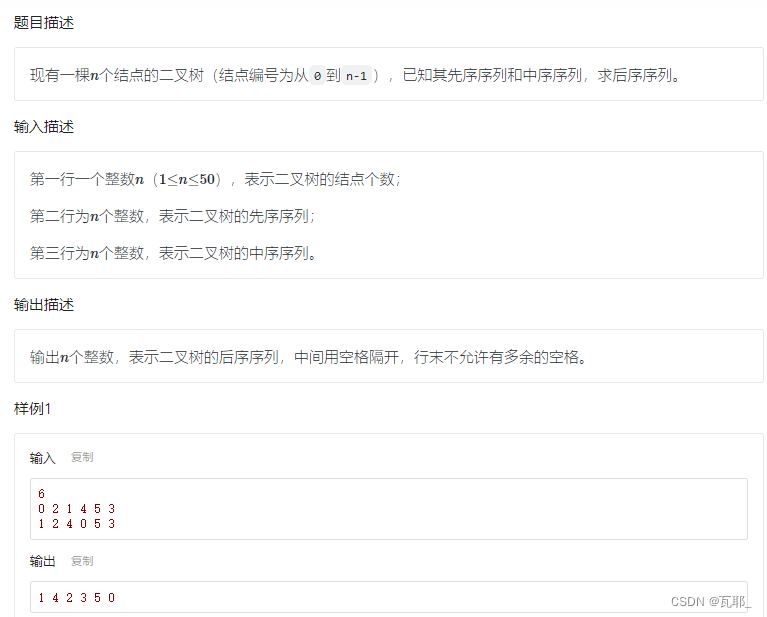
对这道题采用静态链表进行解决,完整代码如下:
#include<cstdio>
const int MAXN = 51;
int rld[MAXN] = {};
int lrd[MAXN] = {};
int count = 1 , n;
struct Node{
int lchild;
int rchild;
}node[MAXN];
void ldr(int root){ //后序遍历
if(root == -1) return;
ldr(node[root].lchild);
ldr(node[root].rchild);
printf("%d", root);
if(count < n) {
printf(" ");
count++;
}
}
int resume(int rldl , int rldr , int lrdl , int lrdr){ //和partition相似
if(rldl > rldr) return -1;
int root = rld[rldl]; //这里散列,将先序序列中找到的根节点元素当成根节点地址
int k;
for(k = lrdl; k <= n - 1; k++)
if(lrd[k] == rld[rldl]) break;
int numl = k - lrdl;
node[root].lchild = resume(rldl + 1 , rldl + numl , lrdl , k - 1); //左子树
node[root].rchild = resume(rldl + numl + 1 , rldr , k + 1 , lrdr); //右子树
return root;
}
int main(){
scanf("%d", &n);
for(int i = 0; i <= n - 1; i++)
scanf("%d", rld + i);
for(int i = 0; i <= n - 1; i++)
scanf("%d", lrd + i);
ldr(resume(0 , n - 1 , 0 , n - 1));
}
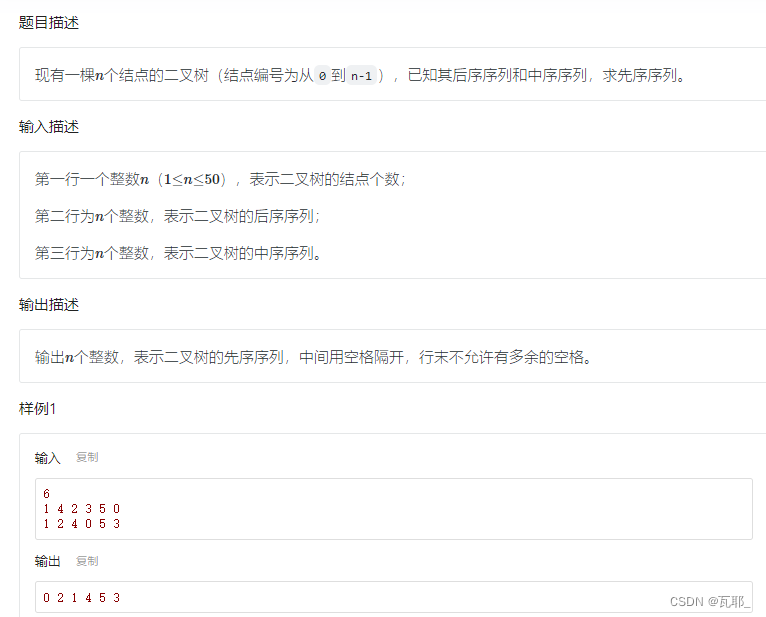
对这道题采用指针法链表实现,完整代码如下:
#include<cstdio>
#include<iostream>
using namespace std;
const int MAXN = 51;
int ldr[MAXN] = {};
int lrd[MAXN] = {};
int count = 1 , n;
struct Node{
int data;
Node* lchild;
Node* rchild;
};
void rld(Node* root){ //先序遍历
if(root == NULL) return;
printf("%d", root -> data);
if(count < n) {
printf(" ");
count++;
}
rld(root -> lchild);
rld(root -> rchild);
}
Node* resume(int ldrl , int ldrr , int lrdl , int lrdr){ //和partition相似
if(ldrl > ldrr) return NULL;
Node* root = new Node;
root -> data = ldr[ldrr];
int k;
for(k = lrdl; k <= n - 1; k++)
if(lrd[k] == ldr[ldrr]) break;
int numl = k - lrdl; //总是先向左走
root -> lchild = resume(ldrl , ldrl + numl - 1 , lrdl , k - 1); //左子树 , 注意个数和序列下标之间的转换
root -> rchild = resume(ldrl + numl , ldrr - 1 , k + 1 , lrdr); //右子树
return root;
}
int main(){
scanf("%d", &n);
for(int i = 0; i <= n - 1; i++)
scanf("%d", ldr + i);
for(int i = 0; i <= n - 1; i++)
scanf("%d", lrd + i);
rld(resume(0 , n - 1 , 0 , n - 1));
}
六、其余小题练习
1.二叉树的高度
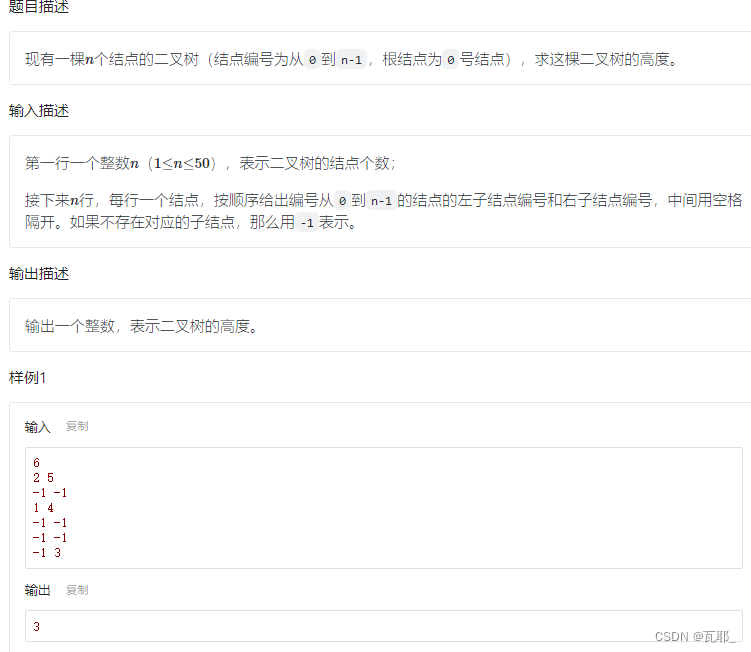
因为二叉树是带有递归性质的,所以求树的高度其实就是求树的最大递归深度,完整代码如下:
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 50;
struct Node {
int l, r;
} nodes[MAXN];
int getHeight(int root) { //递归深度
if (root == -1) {
return 0;
}
int leftHeight = getHeight(nodes[root].l);
int rightHeight = getHeight(nodes[root].r);
return max(leftHeight, rightHeight) + 1; //属于最优解问题,但不具备重叠子问题
}
int main() {
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d%d", &nodes[i].l, &nodes[i].r);
}
printf("%d", getHeight(0));
return 0;
}
2.二叉树的节点层号

这其实就是BFS中的记录层数,在结点中加入计数器变量记录即可,当然也可以采用DFS实现,完整代码如下:
#include<cstdio>
#include<queue>
using namespace std;
const int MAXN = 51;
struct Node{
int lchild;
int rchild;
int step;
}node[MAXN];
void BFS(int root){
queue <int> qe;
qe.push(root);
while(!qe.empty()){
int top = qe.front();
qe.pop();
if(node[top].lchild != -1) {
qe.push(node[top].lchild);
node[node[top].lchild].step = node[top].step + 1;
}
if(node[top].rchild != -1) {
qe.push(node[top].rchild);
node[node[top].rchild].step = node[top].step + 1;
}
}
}
int main(){
int n;
scanf("%d", &n);
for(int i = 0; i <= n - 1; i++)
scanf("%d%d", &(*(node + i)).lchild , &(*(node + i)).rchild);
node[0].step = 1;
BFS(0);
for(int i = 0; i <= n - 1; i++){
printf("%d", node[i].step);
if(i < n - 1) printf(" ");
}
}
3.翻转二叉树

由于二叉树是自身定义自身,所以在输入时,将左右子树的输入顺序调换即可,完整代码如下:
#include<cstdio> //静态二叉链表
const int MAXN = 51;
struct Node{
int lchild;
int rchild;
}node[MAXN];
int count = 1 , n;
void rld(int root){ //先序遍历
if(root == -1) return;
printf("%d", root);
if(count < n) {
printf(" ");
count++;
}
rld(node[root].lchild);
rld(node[root].rchild);
}
void lrd(int root){ //中序遍历
if(root == -1) return;
lrd(node[root].lchild);
printf("%d", root);
if(count < n) {
printf(" ");
count++;
}
lrd(node[root].rchild);
}
void ldr(int root){ //后序遍历
if(root == -1) return;
ldr(node[root].lchild);
ldr(node[root].rchild);
printf("%d", root);
if(count < n) {
printf(" ");
count++;
}
}
int main(){
scanf("%d", &n);
for(int i = 0; i <= n - 1; i++)
scanf("%d%d", &node[i].rchild , &node[i].lchild); //输入时反着输就行了
rld(0);
count = 1;
printf("\n");
lrd(0);
}
4.二叉树的最近公共祖先

这是经典的LCA算法,这里就采用最简单的方法实现了,开一个记录前驱结点的数组,将每个节点的唯一前驱节点记录,最后通过遍历来找到距离两个目标结点最近的祖先节点。这和BFS中的记录路径方法类似,完整代码如下:
#include<cstdio>
const int MAXN = 51;
int pre[MAXN] = {-1}; //初始化根节点
struct Node{
int lchild;
int rchild;
}node[MAXN];
void rld(int root , int k1 , int k2){
if(root == -1) return;
pre[node[root].lchild] = root;
rld(node[root].lchild , k1 , k2);
pre[node[root].rchild] = root;
rld(node[root].rchild , k1 , k2);
}
int main(){
int n , k1 , k2;
scanf("%d%d%d", &n , &k1 , &k2);
for(int i = 0; i <= n - 1; i++)
scanf("%d%d", &node[i].lchild , &node[i].rchild);
rld(0 , k1 , k2);
for(int i = k1; i != -1; i = pre[i]) //反向遍历祖先,第一个相同的祖先就是层数最大的祖先,画画图
for(int j = k2; j != -1; j = pre[j])
if(i == j) {
printf("%d", i);
return 0;
}
}
5.二叉树的左视图序列

把问题简化成用树的语言描述,即输出每一层最左边的元素,转化成层次遍历就是输出每一层的第一个元素,所以采用BFS实现,完整代码如下:
#include<cstdio> //层次遍历,输出每一层最左面的数 ,左视图就先入队左子树,右视图就先入队右子树
#include<queue>
using namespace std;
const int MAXN = 51;
struct Node{
int lchild;
int rchild;
}node[MAXN];
void BFS(int root){
queue <int> qe;
qe.push(root);
int num = 0;
while(!qe.empty()){
int cnt = qe.size(); //这里必须将size()保存在一个int变量中
for(int i = 0; i < cnt; i++){
int top = qe.front();
qe.pop();
if(i == 0) { //不知道长度的情况下就把空格输在元素前面
if(num > 0) printf(" ");
printf("%d", top);
num++;
}
if(node[top].lchild != -1) qe.push(node[top].lchild);
if(node[top].rchild != -1) qe.push(node[top].rchild);
}
}
}
int main(){
int n;
scanf("%d", &n);
for(int i = 0; i <= n - 1; i++)
scanf("%d%d", &node[i].lchild , &node[i].rchild);
BFS(0);
}
七、备注
1.二叉树具有递归定义性质,这一点很重要,意味着树的操作都是基于递归实现的;
2.二叉树是非线性逻辑结构的数据结构,意味着二叉树的遍历采用DFS和BFS实现;























 852
852











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










