【问题描述】
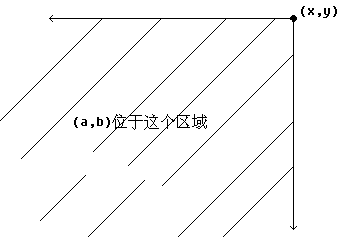
在一个平面上,如果有两个点(x,y),(a,b),如果说(x,y)支配了(a,b),这是指x>=a,y>=b;用图形来看就是(a,b)坐落在以(x,y)为右上角的一个无限的区域内。
给定n个点的集合,一定存在若干个点,它们不会被集合中的任何一点所支配,这些点叫做极大点。请编程找出所有的极大点,按照x坐标由小到大,输出极大点的坐标。
【输入格式】
输入包括两行,第一行是正整数n,表示是点数,第二行包含n个点的坐标,坐标值都是整数,坐标范围从0到100,输入数据中不存在坐标相同的点。
【输出格式】
按x轴坐标最小到大的顺序输出所有极大点。输出格式为:(x1,y1),(x2,y2),…(xk,yk),按x由小到大,x相同则按y由小到达输出。注意:输出的每个点之间有”,”分隔,最后一个点之后没有”,”,少输出和多输出都会被判错。
【输入样例】
5
1 2 2 2 3 1 2 3 1 4
【输出样例】
(1,4),(2,3),(3,1)
【样例解释】
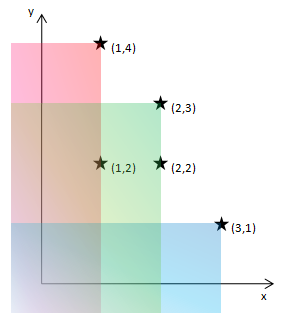
样例的点和极大点的图形如下:
【数据范围】
80%的数据满足:n<=6000
100%的数据满足:n<=100000
【来源】
【思路梳理】
没什么太多好说的,仔细想想就会发现用O(n)的算法就可以直接得出解,动态规划都不需要,简单讲解一下:
对于这种平面上的双关键字,肯定是让其中的一维有序,因为题目要求的是按照x横坐标升序输出,那么推荐sort的时候按照x关键字从小到大排序,否则的话输出时要再按照x从小到大的顺序输出,徒劳。
当x横坐标有序的时候,按照动态规划的思想就可以将样例简化为序列4,2,3,2,1,考察答案,选择了第一、三、五个点,不难发现就是求最长的严格递减序列上的各个点。也就是说用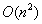
给出一种可行而高效的搜索思路:设置数组t[i]=在下标为i~n的所有点中,纵坐标最大的点的纵坐标y。显然,在对于任意一个点a[i]是否能够成为极大点的考察的时候,如果t[i+1]>=a[i].y那么该点i不能成为极大点(在下标为i+1~n的点中至少存在一个点,其纵坐标不小于i点的纵坐标,如果其后面某一个点a[j]纵坐标与a[i]相等,那么根据题目表述,整个x<=a[j].x,y<=a[j].y都会被控制,包括了同一纵行上的所有点)。直接给出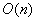
【Cpp代码】
#include<cstdio>
#include<iostream>
#include<algorithm>
#define maxn 100005
#define inf 100005
using namespace std;
int n,d[maxn],t[maxn];
bool mark[maxn];
struct data
{
int x,y;
friend bool operator<(data a,data b)
{return a.x==b.x?a.y<b.y : a.x<b.x;}
}a[maxn];
void dp()
{
//mark[i]=true(if a[i].y>t[i+1])
//t[i]=编号为i至n的点中,纵坐标最大的点的纵坐标
for(int i=n;i>=1;i--) d[i]=-inf,t[i]=max(t[i+1],a[i].y);
for(int i=1;i<=n;i++)if(a[i].y>t[i+1]) mark[i]=true;
bool ok=true;
for(int i=1;i<=n;i++)if(mark[i])
{
if(ok) ok=false,printf("(%d,%d)",a[i].x,a[i].y);
else printf(",(%d,%d)",a[i].x,a[i].y);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].x,&a[i].y);
sort(a+1,a+1+n);
dp();
return 0;
}























 11万+
11万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








