1、分治策略,递归地求解 一个问题,在 每层递归中应用 如下三个步骤:
分解 步骤 将问题划分为一些子问题,子问题的形式 与 原问题一样,只是规模更小
解决 步骤 递归地 求解出子问题。如果 子问题的规模足够小,则停止递归,直接求解
合并 步骤将子问题的解 组合成 原问题的解
当子问题足够大,需要 递归求解时,称之为 递归情况;当子问题变得足够小,不再需要 递归时,表示 递归已触底,进入了 基本情况
2、递归式 可以自然地刻画 分治算法的运行时间。一个递归式 就是一个等式 或 不等式,它通过 更小的输入上的函数值 来描述一个函数
比如,第二章 3.2描述的 合并过程的最坏情况运行时间T(n)
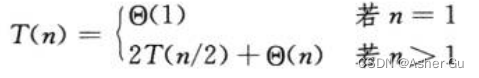
求解可得 T(n) = Θ(nlgn)
递归式 可以有很多形式。例如:一个递归算法 可能将问题划分为 规模不等的子问题,如 2/3对1/3 的划分。如果 分解和合并步骤 都是线性时间的,这样的算法 会产生递归式 T(n) = T(2n/3) + T(n/3) + Θ(n)
子问题的规模 不必是 原问题规模的一个 固定比例。比如 线性查找的递归版本 仅生成一个子问题,其规模 仅比 原问题的规模 少一个元素。每次 递归调用 将花费常量的时间 再加上 下一层递归调用的时间(想到 第二章的递归树),因此 递归式为 T(n) = T(n-1) + Θ(1)
介绍 三种求解递归式的方法(算出 算法的Θ或O渐近界的方法)
1)代入法 猜测一个界,用 数学归纳法 证明这个界 是正确的
2)递归树法 将 递归式转换成 一棵树,其结点 表示不同层次的递归调用 产生的代价(拆分+合并代价)。然后 使用 边界和(每层和相加)来求解递归式
3)主方法 求解 形如 T(n) = aT(n/b) + f(n) 的递推式的界,其中 a>=1,b>1,f(n)是一个给定的函数
这种形式的递归式 刻画了这样的分治算法:生成 a个子问题,每个子问题的规模是 原问题规模的 1/b,分解 和 合并步骤 总共花费时间为 f(n)
当遇到 不等式的递归式时,例如:T(n) <= 2T(n/2) + Θ(n) 因为 这样一种递归式 仅描述了T(n)的一个上界,因此可以用 大O符号 而不是 Θ符号来描述其解;如果换成 大于等于,递归式只给出了 下界,应使用 Ω符号 来描述其解
3、忽略递归式 声明和求解 的一些技术细节
1)忽略 向下取整、向上取整。比如 第二章归并排序,考虑n为奇数的情况,描述合并过程 最坏情况运行时间的 准确递归式为
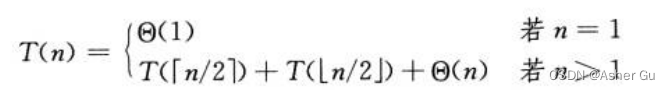
但是 求解的时候使用

2)边界条件 是另一类 通常忽略的细节。出于方便,一般忽略递归式的边界条件,假设 对很小的n,T(n)为常量
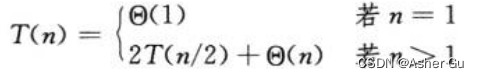
所以被表示为

去掉了n很小的时候 函数值的显性描述。虽然 改变T(1)的值 会改变递归式的精确解,但是 改变幅度不会超过一个 常数因子,因而 函数的增长阶不会变
当 声明、求解 递归式时,常常忽略 向下取整、向上取整 及 边界条件。先忽略这些细节,再确定 这些细节对结果 是否有大的影响
1、最大子数组问题
买一次股票收益最大化:有的时候 最大收益 既不是在 最低价格时买进,也不是在 最高价格时卖出
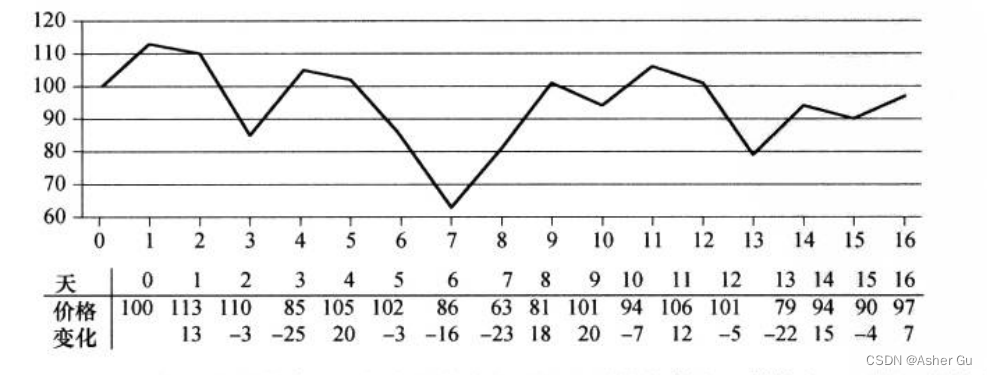
1、暴力求解方法
尝试每种买入卖出组合,n天中有Cn2种 日期组合,因为 Cn2 = Θ(n2),而处理每对日期 所花费的时间 至少也是 常量,因此 这种方法的运行时间为 Ω(n2)
2、问题变换
目标是 寻找一段日期,使得 第一天到最后一天的股票价格 净变值最大。所以 不再从 每日价格的角度 去看待输入数据,而是 考察每日价格的变化,第i天的价格变化 定义为 第i天 和 第i-1天的价格差。表格的最后一行 给出了每日价格变化,把这一行看成 数组A,问题转化为
寻找A的和最大的 非空连续子数组,称这样的连续子数组 为 最大子数组
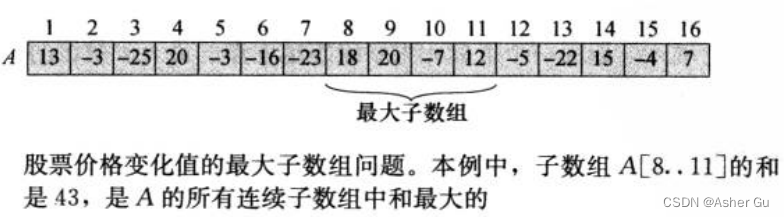
计算所有 Θ(n2) 个子数组和时,可以 利用之前计算出的子数组和 来计算 当前子数组的和,使得 每个子数组和的计算时间为 O(1),从而 暴力求解方法花费的时间 Θ(n2)
3、使用 分治策略的求解方法
将子数组 划分为 两个规模尽量相等的子数组,找到 子数组的中央位置,然后 考虑求解两个子数组 A[low…mid]和A[mid+1…high]
A[low…high] 的任何连续子数组 A[i…j] 所处的位置 必然是 以下三种情况之一:
1)完全位于 子数组A[low…mid]中,因此 low <= i <= j <= mid
2)完全位于 子数组A[mid+1…high]中,因此 mid < i <= j <= high
3)跨越了中点,因此 low <= i <= mid < j <= high
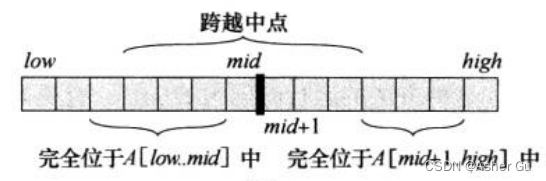
A[low…high]的最大子数组 必然是 完全位于 A[low…mid]中、完全位于 A[mid+1…high]中 或者 跨越中点的所有子数组中 和的最大者。可以递归地求解 A[low…mid] 和 A[mid+1…high]的最大子数组,这两个子问题 仍是 最大子数组问题,只是 规模更小
剩下的就是 寻找跨越中点的最大子数组,在三种情况中 选取和最大者
对于跨越中点的最大子数组,只需要 找出形如A[i…mid] 和 A[mid+1…j]的最大子数组,将其 合并即可
FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)
left-sum = -inf
sum = 0
for i = mid downto low
sum = sum + A[i]
if sum > left-sum
left-sum = sum
max-left = i
right-sum = -inf
sum = 0
for j = mid to high
sum = sum + A[j]
if sum > right-sum
right-sum = sum
max-right = j
return (max-left, max-right, left-sum + right-sum)
最后返回 子数组的边界下标 以及 子数组的和
子数组A包含 n个元素,调用 FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high) 花费 Θ(n)的时间
由于 两个for循环的每次迭代花费 Θ(1)时间,总迭代次数为

设计 求解最大子数组问题的 分治算法的伪代码

4、分治算法的分析
建立一个 递归式来描述 递归过程 FIND-MAXIMUM-SUBARRAY的运行时间
像分析 归并排序一样,对问题进行简化,假设 原问题的规模为2的幂。用T(n)表示 FIND-MAXIMUM-SUBARRAY 求解n个元素的 最大子数组的运行时间
对于n=1的基本情况,T(1) = Θ(1)
当 n>1 时为递归情况,解决两个子问题:左子数组 和 右子数组,求解时间均为 T(n/2)。分解时间为 Θ(1),第6行调用 FIND-MAX-CROSSING-SUBARRAY花费 Θ(n)时间,第7-11行 花费 Θ(1) 时间
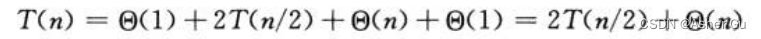
综合T(1) = Θ(1) 以及 上式,T(n)的递归式:
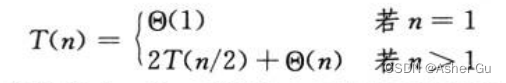
主方法 求解递归式,其解为 T(n) = Θ(nlgn),优于暴力法
2、矩阵乘法的Strassen算法
普通矩阵相乘,A,B都是 n×n 的方阵
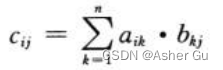

由于 三重for循环的每一重 都恰好执行n步,第7行 每次执行花费 常量时间,因此 过程 SQUARE-MATRIX-MULTIPLY 花费 Θ(n3) 时间
Strassen n×n矩阵相乘的递归算法,运行时间为 Θ(nlg7),由于 lg7 在2.80 和 2.81之间,因此 Strassen算法的运行时间为 O(n2.81),渐近复杂性优于 简单的 SQUARE-MATRIX-MULTIPLY 过程
2.1 简单的分治算法(58)
1、计算矩阵 C = A·B 时,假定三个矩阵 均为n×n矩阵,其中 n为2的幂(保证分解后为整数)
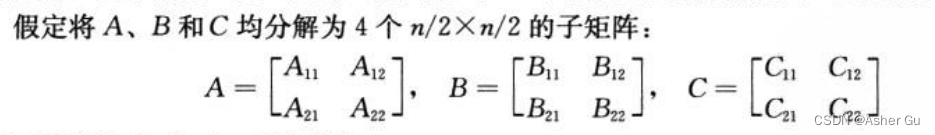
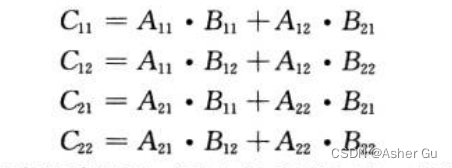
每个公式对应 两对 n/2×n/2 矩阵的乘法 及 n/2 × n/2 积的加法
利用公式设计 直接的递归分治算法:
SQUARE-MATRIX-MULTIPLY-RECURSIVE(A, B)
n = A.rows
if n == 1
c11 = a11 · b11
else 把A,B,C分解成4个 n/2×n/2 的子矩阵
C11 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A11, B11) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A12, B21)
C12 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A11, B12) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A12, B22)
C21 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A21, B11) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A22, B21)
C22 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A21, B12) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A22, B22)
第5行 应该如何分解矩阵?如果创建 12个新的 n/2×n/2 矩阵,将会花费 Θ(n2) 时间复制矩阵元素
不复制矩阵,使用下标计算,执行分解 只需要Θ(1)的时间
2、推导递推式 刻画 SQUARE-MATRIX-MULTIPLY-RECURSIVE的运行时间
对n = 1的情况下,只需要进行 一次标量乘法(c11 = a11 · b11)因此 T(1) = Θ(1)
对n > 1的情况下,使用下标分解矩阵 花费Θ(1)时间,共8次 递归调用 SQUARE-MATRIX-MULTIPLY-RECURSIVE,每次调用完成 两个n/2×n/2矩阵的乘法,总时间为 8T(n/2)
同时还需要计算 4次矩阵加法,每个矩阵 包含n2/4个元素,因此 每次矩阵加法花费 Θ(n2)时间,矩阵加法的次数 是常数,总时间为 Θ(n2)
递归情况的总时间 为分解时间、递归调用时间 及 矩阵加法时间 之和

如果 通过复制元素来实现分解,额外开销 Θ(n2),递归式 不会发生改变,运行总时间 将会提高常数倍
SQUARE-MATRIX-MULTIPLY-RECURSIVE运行时间的递归式
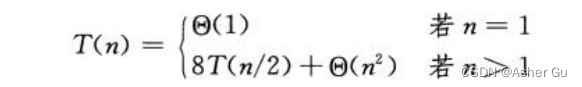
利用 主方法求解 递归式,得到的解是 T(n) = Θ(n3)
简单的分治法 并不优于 直接的 SQUARE-MATRIX-MULTIPLY过程
对于分解和合并过程,分解两个矩阵,进行4次相加 都可以省略 常数因子,但是 当分析8次递归调用时,就不能 简单省略 常数因子8了。原因可以 通过递归树来理解,因子8 决定了树中每个节点 有几个孩子节点,进而决定了 树的每一层为 总和贡献了多少项,如果 省略,递归树 就变成 线性结构
渐近符号 包含了常数因子,但 递归符号(如 T(n/2)) 并不包含
2.2 Strassen方法(60)
1、方法的核心思想是 令递归树稍微 不那么茂盛一点,只 递归7次 而不是8次 n/2×n/2矩阵的乘法。减少 一次矩阵乘法 带来的代价 可能是额外几次 n/2×n/2 矩阵的加法,但只是常数次
2、Strassen算法 运行时间T(n) 的递归式
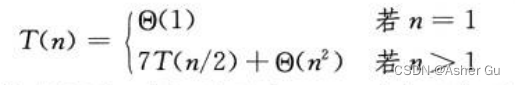
用常数次 矩阵乘法的代价 减少了一次 矩阵乘法(必须进行10次 n/2×n/2 矩阵的加减法),此递归式的解为 T(n) = Θ(nlg7)
3、求解递归式
3.1 代入法 求解递归式(62)
1、代入法求递归式 分两步:
1)猜测 解的形式
2)用 数学归纳法 求出解中的常数,并证明 解是正确的
可以用 代入法 为递归式 建立上界或下界
例如:确定下面递归式的上界
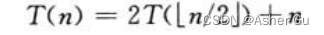
该递归式与 之前的2中的递归式 相似,猜测其解为 T(n) = O(nlgn)。代入法要求证明,由常数 c>0,可有 T(n)<=cn lgn。首先假定 此上界对所有正数 m<n 都成立,特别是对于m = ⌊n/2⌋(右边出现的符号),有T(⌊n/2⌋) <= c⌊n/2⌋lg(⌊c/2⌋),带入递归式

只要 c>=1,最后一步 都会成立
数学归纳法 要求我们 证明解在边界条件下 也成立。对于 归纳证明,边界条件 适合作为 基本情况。我们必须证明,通过选择足够大的常数c,可以使得 上界T(n) <= cn lgn对边界条件也成立
假设T(1) = 1是递归式 唯一边界条件,但是对于n=1,边界条件 T(n) <= cn lgn 推导出 T(1) <= c1 lg1 = 0,与T(1) = 1矛盾,因此 归纳证明 不成立
要克服这个障碍,对 特定的边界条件证明归纳假设成立。渐近符号 仅要求我们对 n>=n0 证明 T(n) <= cn lgn,其中 n0 是我们 可以自己选择的常数
首先观察到 对于 n>3,递归式并不直接依赖于 T(1),将归纳证明中的 基本情况 T(1) 替换成 T(2) 和 T(3),并令 n0=2
任何 c>=2 都能保证 n=2 和 n=3 的基本情况成立
拓展边界条件 使归纳假设对较小的n成立,是一种 简单直接的方法
2、做出好的推测:
1)使用 递归树
2)要求解的递归式 与曾经见过的递归式相似,那么 猜测一个类似的解是合理的
如: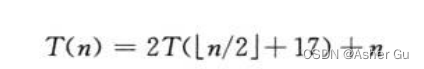
在等式的右边加了个17,当n较大时,⌊n/2⌋和⌊n/2⌋+17差距不大:都是接近n的一半。因此 猜测T(n)=O(n lgn)
3)另一种 做出好的猜测的方法是 先证明递归式较松的上下界,然后 缩小不确定的范围
比如对于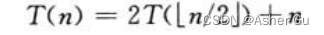
可以从下界 T(n)=Ω(n) 开始,因为递归式中 包含n这一项,还可以 证明一个初始上界 T(n) = O(n2),然后可以逐渐降低上界,提升下界,直至 收敛到渐近紧确界 T(n) = Θ(n lgn)
3、正确猜出了 递归式解的 渐近界,但莫名其妙 在归纳证明时 失败了:问题常常出在 归纳假设不够强,无法 证出准确的界。当遇到这种障碍时,如果 修改猜测,将它减去 一个低阶的项,数学证明 常常能顺利进行
如: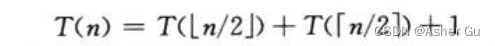
猜测解为 T(n) = O(n),尝试证明 对某个恰当选出的常数c,T(n) <= cn 成立
将猜测带入递归式,得到: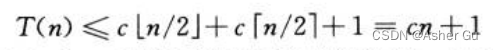
这并不意味着 对任意c都有 T(n) <= cn,可能忍不住尝试 一个更大的界(如T(n) = O(n2))
但其实原来的假设 T(n) = O(n) 是对的,必须做出更强的假设
直觉上猜测是接近正确的:只差一个常数1,一个低阶项。除非 证明与归纳假设严格一致的形式,否则 数学归纳法还是会失败。克服 这个困难的方法 是从先前的猜测中 减去一个低阶项,新的猜测是 T(n) <= cn-d
减去一个低阶项的想法 与直觉是相悖的。但是 更松的界 难道不是更容易证明?不一定
实际上 更弱的上界 可能会更困难,因为 为了证明更弱的上界,在归纳证明中 也必须使用同样更弱的界。当递归式 包含超过一个递归项时,将猜测的界 减去一个低阶项 意味着 每次对每个递归项 都减去一个低阶项
上例中 对 T(⌊n/2⌋) 以及 T(⌈n/2⌉)分别减去 d,以不等式 T(n) <= cn - 2d + 1结束,可以 很容易找到一个d,使得 cn-2d+1 小于等于 cn-d
4、避免陷阱:错误地证明 T(n) = O(n):
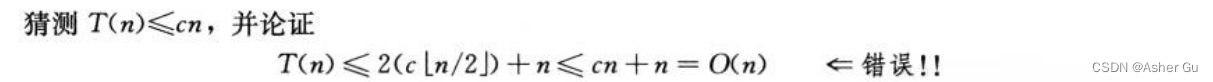
错误在于 并未证出与归纳假设 严格一致的形式,即T(n) <= cn。当要证明 T(n) = O(n) 时,需要显式地证出 T(n) <= cn
5、改变变量:即变量代换
如: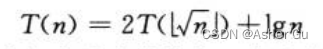
不必担心值的舍入误差 问题,只考虑√n是整数的情形即可。令 m = lgn
得到:T(2m) = 2T(2m/2) + m
重命名 S(m) = T(2m),得到:S(m) = 2S(m/2) + m
这与递归式 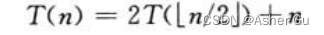 很像,确实有相同的解:S(m) = O(m lgm)
很像,确实有相同的解:S(m) = O(m lgm)
从S(m) 转换回 T(n),得到 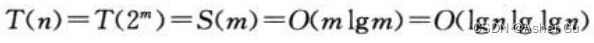
3.2 用递归树方法 求解递归式(65)
1、递归树中,每个节点 表示单一子问题的代价,子问题 对应某次递归函数调用。将树中 每层中的代价求和,得到 每层代价,然后 将所有层的代价求和,得到 所有层次的递归调用的 总代价
2、递归树 最适合用来生成好的猜测,然后 即可用 代入法 来验证猜测是否正确
以 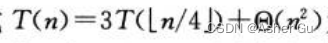 为例 如何使用递归树生成 一个好的猜测。首先关注 如何寻找解的一个上界。舍入对求解递归式 通常没有影响,因此可以为递归式
为例 如何使用递归树生成 一个好的猜测。首先关注 如何寻找解的一个上界。舍入对求解递归式 通常没有影响,因此可以为递归式 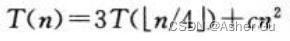 创建一颗递归树,其中 已将渐近符号 改写为 隐含的常数系数 c>0
创建一颗递归树,其中 已将渐近符号 改写为 隐含的常数系数 c>0
假定n是4的幂(可以忍受不精确),所有子树的规模 均为正数。根节点的cn2项 表示递归调用顶层的代价,根的三棵子树 表示规模为 n/4 的子问题所产生的代价
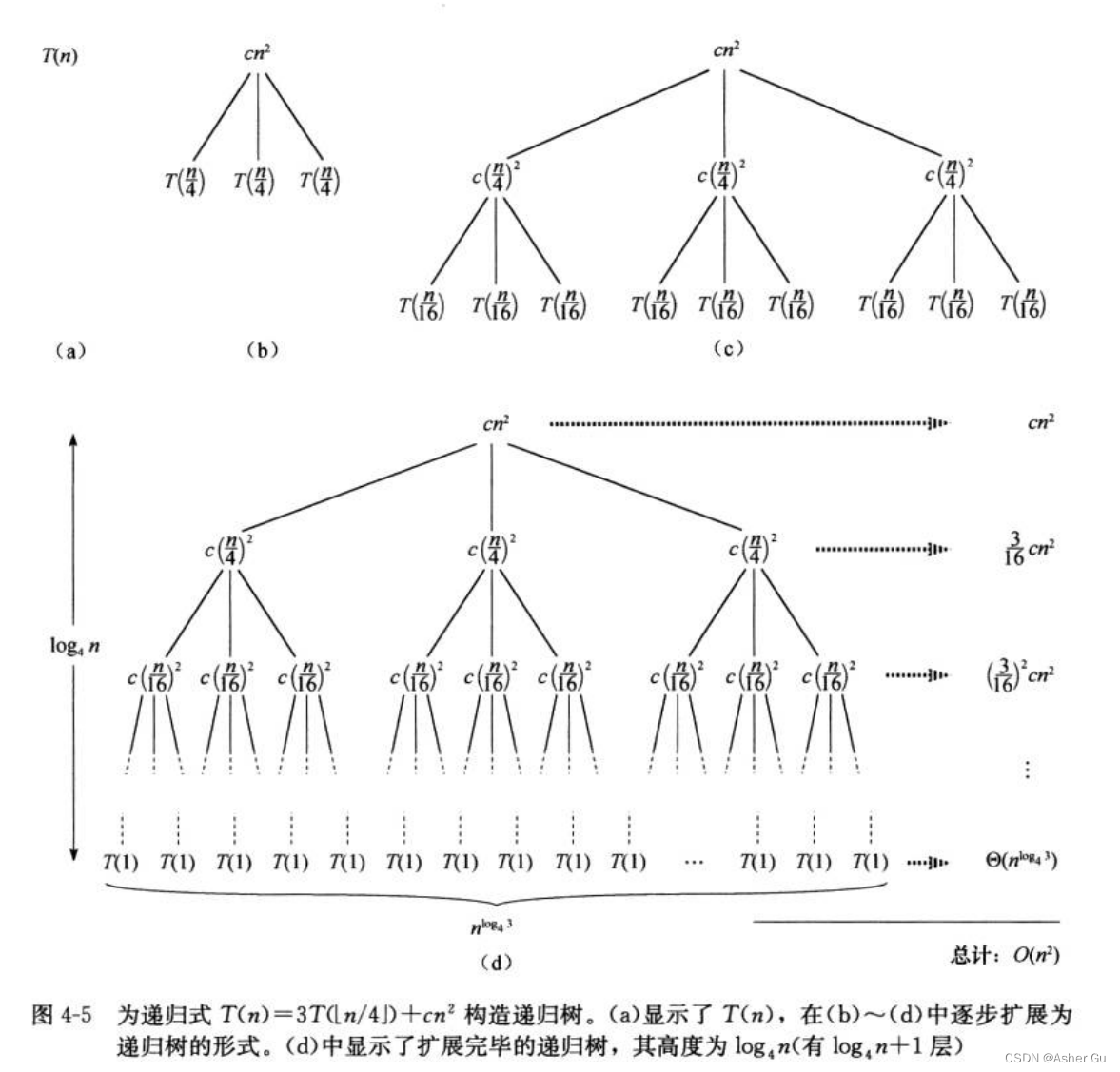
子问题的规模 每一步减少为上一步的1/4,所以 最终必然会 达到边界条件。深度为i的节点 对应规模为 n/4i的子问题(每一层子问题规模 都是上一层的1/4)。当 n/4i = 1时 子问题规模变为1,因此 递归树有log4n + 1层
对于 树的每一层的代价。每层的结点数 都是上层的3倍,深度为i的结点数为3i。深度为i的每个结点的代价为 c(n/4i)2。深度为i的每个结点的总代价为 3ic(n/4)2=(3/16)icn2。树的最底层深度为 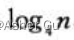 有
有 个节点,每个结点的代价为 T(1),总代价为
个节点,每个结点的代价为 T(1),总代价为  ,即
,即 
求所有层次的代价之和,确定整棵树的代价
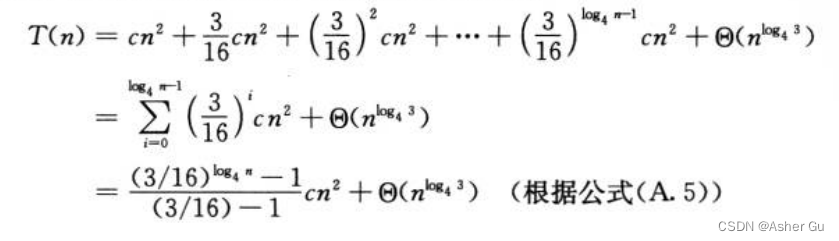
再次利用一定程度的不精确,利用 无限递减几何级数 作为上界,回退一步

推导出了一个猜测 T(n) = O(n2)
实际上,如果 O(n2) 确实是 递归式的上界,它必然是 一个紧确界。第一次调用的代价是 Θ(n2) ,因此 Ω(n2) 必然是 递归式的 一个下界
现在用 代入法 验证猜测 T(n) = O(n2) 是递归式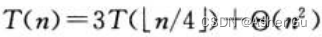 的一个上界 是正确的,希望证明 T(n) <= dn2对 某个常数 d>0 成立。使用常数 c>0
的一个上界 是正确的,希望证明 T(n) <= dn2对 某个常数 d>0 成立。使用常数 c>0
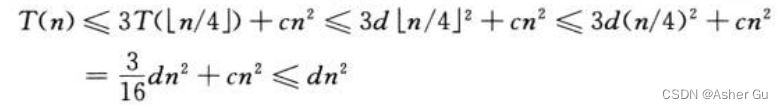
当  时,最后一步推导成立
时,最后一步推导成立
3、更复杂的例子
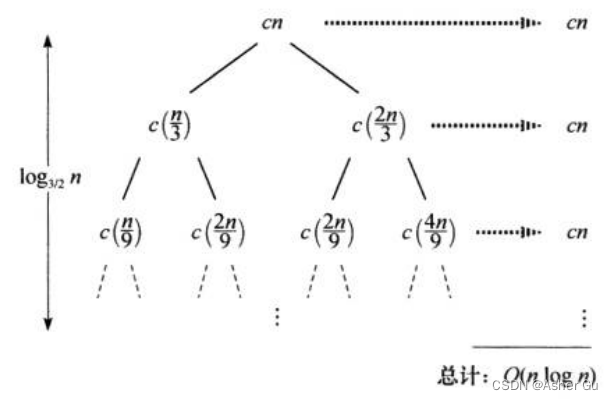
上图显式了递归 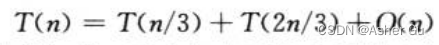 的递归树
的递归树
求代价之和时,发现每层的代价均为 cn。从根到叶 的最长简单路径是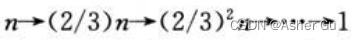 由于当
由于当 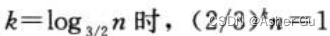 因此树高为
因此树高为
直觉上 期望递归式的解 最多是 层数乘以每层的代价,并不是递归树中 每个层次的代价都是 cn。如果 递归树是一棵高度为  的完全二叉树,则 叶节点的数量应为
的完全二叉树,则 叶节点的数量应为  。由于每个结点的代价为常数,叶节点代价的总和是Ω(n lgn)。但递归树 并不是完全二叉树,叶节点的数量小于
。由于每个结点的代价为常数,叶节点代价的总和是Ω(n lgn)。但递归树 并不是完全二叉树,叶节点的数量小于 。当从根结点 逐步往下走时,越来越多的内结点 是缺失的。但是 只是希望得到一个猜测 用于 代入法,还是忍受一些不精确,尝试证明猜测的上界 O(nlgn) 是正确的
。当从根结点 逐步往下走时,越来越多的内结点 是缺失的。但是 只是希望得到一个猜测 用于 代入法,还是忍受一些不精确,尝试证明猜测的上界 O(nlgn) 是正确的
用代入法验证 O(nlgn) 是递归式解的一个上界,来证明 T(n) <= dn lgn
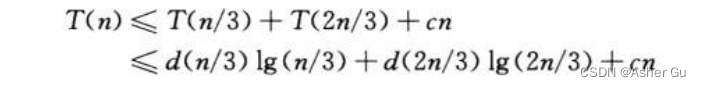
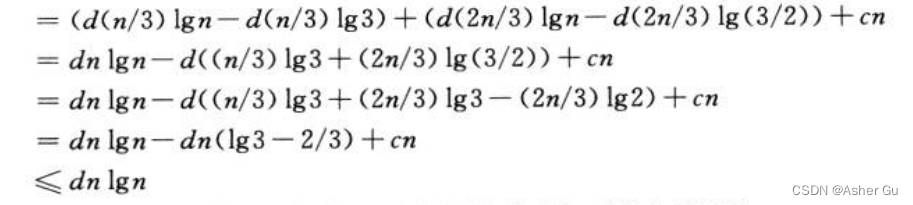
只要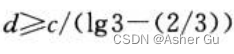
3.3 用主方法 求解递归式
1、主成分为形如 T(n) = aT(n/b) + f(n) 提供了 流程型的求解方法,其中 a>=1 和 b>1 是常数,f(n) 是渐近正函数
对于式子 T(n) = aT(n/b) + f(n) :将规模为n的问题 分解为 a个子问题,每个子问题规模为 n/b。a个子问题 递归地进行求解,每个花费时间 T(n/b),函数f(n)包含了 问题分解 和 子问题解合并 的代价
同时将 a 项 T(n/b) 都替换为 T(⌊n/b⌋) 或 T(⌈n/b⌉) 并不会影响 递归式的渐近性质
2、主定理
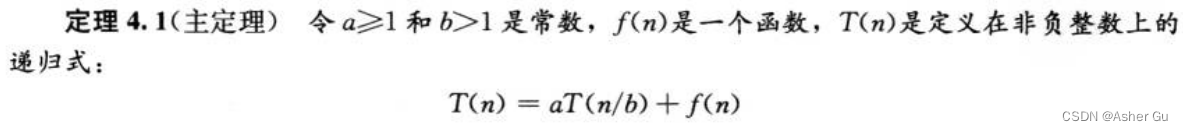

直觉上,对于 三种情况的每一种,将函数 f(n) 与函数 nloga(b) 进行比较。两个函数的较大者 决定了递归式的解。若函数nloga(b)更大,如 情况一,则解为  。若函数f(n)更大,如 情况三,则解为 T(n) =
。若函数f(n)更大,如 情况三,则解为 T(n) =  。若 两个函数大小相当,如 情况二,则乘上一个 对数因子,解为
。若 两个函数大小相当,如 情况二,则乘上一个 对数因子,解为 
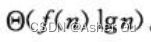
技术细节上,在第一种情况中,不是 f(n) 小于 nlogb(a)就够了,而是要 多项式意义上的 小于,也就是说,f(n) 必须渐近小于 nlogb(a),要相差一个因子 nɛ,其中ɛ是大于0的常数。在第三种情况中,不是 f(n) 大于 nlogb(a)就够了,而是要在 多项式意义上的 大于,而且 还要满足正则条件 af(n/b) <= cf(n)
这三种情况并未覆盖 f(n) 的所有可能性。情况1 和 情况2 / 情况2 和 情况3 之间有一定空隙,f(n) 可能小于 nlogb(a)但不是多项式意义上的 小于 / 大于
3、使用主方法:只需要确定 主定理的哪种情况成立,即可得到解
1)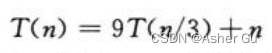
由于 f(n) = O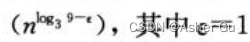 ,因此 可以使用 主定理的情况一,从而 得到解 T(n) = Θ(n2)
,因此 可以使用 主定理的情况一,从而 得到解 T(n) = Θ(n2)
2)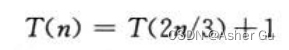
由于 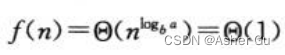 ,因此应用 情况二,从而得到解 T(n) = Θ(lgn)
,因此应用 情况二,从而得到解 T(n) = Θ(lgn)
3)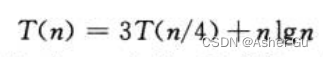
由于 因此,如果可以证明 正则条件成立,即可应用 情况三。当n足够大时,对于 c=3/4,
因此,如果可以证明 正则条件成立,即可应用 情况三。当n足够大时,对于 c=3/4,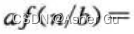
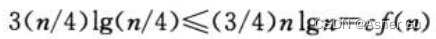 因此,由情况三,递归式的解为 T(n) = Θ(n lgn)
因此,由情况三,递归式的解为 T(n) = Θ(n lgn)
4)主方法 不能用于 如下递归式: 这个递归式看起来 有恰当的形式
这个递归式看起来 有恰当的形式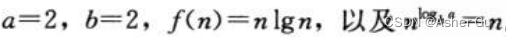 仍然不能用情况三,因为它不是 多项式意义上的大于。比值
仍然不能用情况三,因为它不是 多项式意义上的大于。比值 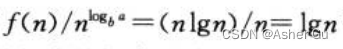 都渐近小于nɛ
都渐近小于nɛ
3.4 证明主定理(70)
见书55页






















 371
371











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








