智源青年科学家袁洋：机器学习可靠性与算法优化的方法探索

2020年2月11日，在“智源论坛Live | 青年科学家线上报告会”上，智源青年科学家、清华大学助理教授袁洋作了题为《机器学习可靠性与算法优化》的演讲。袁洋，2018 年获得康奈尔大学计算机专业博士学位，在机器学习理论与算法设计方面取得了突出成果。他参与合作的关于SGD 逃离鞍点的论文是机器学习理论顶级会议COLT 最近5 年来被引用次数最多的论文，并独立证明了第一个满足严格鞍点性质的函数，即张量分解问题；此外，袁洋还与他人合作给出了第一篇SGD 在非线性网络的收敛性分析。

 

本次讲座，袁洋主要从三大研究方向:机器学习理论、机器学习可靠性、机器学习与算法优化为大家做了精彩的阐述。在机器学习理论方向，袁洋和大家分享了随机梯度下降法（SGD）的理论分析和神经网络收敛性分析的一些结果；在机器学习可靠性方向，袁洋主要的工作和本次的分享主要集中在对抗样本和鲁棒性的研究；对于机器学习与算法优化方向，他认为虽然这其实是两个方向的结合，但是二者是互相帮助的，我们可以用算法、用理论的方式，来解决机器学习的一些问题，同时也可以用机器学习的技术来改进已有的传统算法获得更好的效果。

整理：钱小鹅

编辑：王炜强

机器学习理论

 

机器学习理论的基础分为三个方面，表达能力理论（Representation）、优化理论（Optimization）、泛化理论（Generalization），这三个方向目前都有很多很有意义的研究，袁洋的主要方向是优化理论，也会涉及一点泛化理论的内容。本次讲座，我们主要介绍给大家SGD方法的一些性质，重点是SGD逃离鞍点的工作，也会谈及SGD逃离局部最优点分析、两层神经网络收敛性分析以及对未来的研究构想，下面我们从这四个方向分别为大家整理说明。

 

SGD逃离鞍点[Ge, Jin, Huang, Yuan, COLT’15]

深度学习从某种角度看，可分成两个步骤：第一步，针对具体一个问题来设计好的网络结构，使得这个网络结构能对应解决我们要解决的问题；第二步，考虑使用随机梯度下降法（SGD）或者其变体进行优化。例如：在机器视觉领域，包括图像分类、风格迁移等，我们首先设计好的卷积网络结构，接着使用SGD去做数值优化；Alphago围棋对决，也是使用强化学习、卷积网络以及蒙特卡洛树搜索后使用SGD做优化；同样自然语言处理中一般是Transformer网络和SGD的组合算法。因此，袁洋认为机器学习如同一列很长的列车，卷积网络、强化学习等各种不同的算法可以看成是一节节不同的车厢，而SGD优化方法，如同整个火车的引擎，最终拖着不同的算法达到最后目的地，因此深刻理解SGD是非常重要的。

图1：SGD在机器学习中如同引擎

首先，我们介绍SGD的“祖师爷”-GD，也就是所谓的梯度下降法。在机器学习中，梯度下降的目标是优化一个损失函数L，数学表达式即为：

优化方法是简单的迭代：

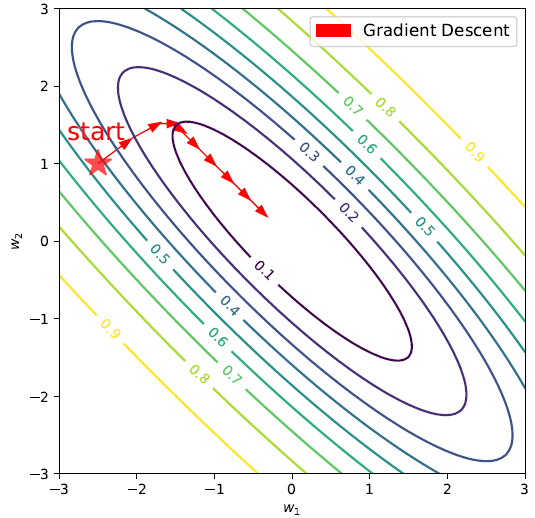
图2:  梯度下降法

如图2所示，迭代函数是个二维函数，从随机点做梯度下降的话，如果每一步都选择函数的严格梯度，逐步迭代后最终会找到函数的全局最优点。虽然GD算法的理论知识非常简单，图示也很直观，但是却有两个局限性：

1.（从应用角度来看）计算

非常慢：需要扫遍所有数据；如果数据很多，就会很慢。

2.（从理论角度来看）可能会卡在稳定点（导数为0的点）上，如图3中我们不难看出，有三个点是导数为0的点。虽然这三个点导数都是0，但是只有中间的点是全局最优点，而左边是鞍点，右边是局部最优点。有理论工作指出，当使用GD算法的话，有可能需要指数时间才能逃离鞍点[Du,Jin, Lee, Jordan, Poczos, Singh, NeurIPS’17]。

图3: L(w)函数图